Файл: Комбинатрные чсла и многочлНЫ.docx

КОМБИНАТРНЫЕ ЧСЛА И МНОГОЧЛНЫ, общее название специ‐ альных чисел и многочленов, которые играют важную роль в решении комбинаторных задач. Как правило, комбинаторные числа имеют нагляд‐ ную комбинаторную интерпретацию (зачастую не единственную), выра‐ жаемую в терминах числа способов выбора и расположения элементов некоторого, обычно конечного, множества, приводящих к конфигураци‐ ям данного класса или числа объектов из некоторого множества объек‐ тов, обладающих тем или иным выделенным свойством.

Простейшими примерами комбинаторных чисел являются числа сочета‐ ний, размещений и перестановок. Если имеется множество из N разл. элементов, то его подмножества называются сочетаниями, число разл. со‐ четаний размера k равно


N(N − 1) … (N − k + 1)

k!


=


N!

k!(N − k)!


.




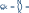
Числа (^N ), k = 0, 1, . . . , N, называют биномиальными коэффициента‐ ми, поскольку они входят в формулу Ньютонабинома. Упорядоченные наборы из разл. элементов множества N называются размещениями, число разл. размещений размера k равно

k
A^k = k!C^k = N(N − 1) … (N − k + 1).

N N
В случае N = k размещения называются перестановками, число всех пе‐ рестановок из N элементов равно PN = N!, где

N! = N(N − 1). . .2 ⋅ 1. Сочетания, размещения и перестановки исполь‐ зуются в разл. разделах математики.
Если допускаются повторения элементов, то число всех сочетаний разме‐


N−k+1
ра k из N разл. элементов равно C^k , а число всех упорядоченных

наборов размера k равно N ^k. Эти числа используют при нахождении ве‐ роятностей разл. событий при классич. определении вероятности (см. Ве‐роятностейтеория). Напр., если имеется урна с N шарами, занумерован‐ ными числами 1, 2, . . . , N , причём шары с номерами 1, 2, . . . , M белого цвета, а остальные – чёрного, то вероятность получить ровно m белых шаров при случайном выборе из урны n шаров равна

_Cm _Am _An−m _Cm _Cn−m

ⁿ M N−M ₌ⁿ N−M _,


C

A
n n

N N
если выбор производится без возвращения шаров, и равна

n _m(
C^m M ^m (N − M)^n−m


_N n

n
= C
M ^m M 1 −

N

N
n−m

(

)

)
при выборе с возвращением.
Из числа более специальных комбинаторных чисел наиболее часто ис‐ пользуются т. н. числа Каталана

числа Моргана

C_n =

1 _n


C ;
n + 1 ²ⁿ

Δⁿ = Δⁿ x^k_∣

n

⁼ ∑⁽⁻¹)^jC^{j(k − j})^n,

k x=0

k

j=0

где Δ – оператор разности Δf(x) = f(x + 1) − f(x); числа Стирлинга

S(n, k) и σ(n, k) соответственно 1-го и 2-го рода; числа Белла
n

B_n = ∑ S(n, k).

k=0
Все эти числа, как правило, имеют наглядные комбинаторные интерпре‐ ^{тации. Так, напр., число Каталана} C_n ^{равно числу векторов}

i=1

k
(ε₁, . . . , ε_2n), ε_i = ±1, i = 1, . . . , 2_n , таких, что ∑^k

ε_i ≥ 0, k = 1, . . . ,

i=1

i
2n − 1, ∑²ⁿ ε

= 0; число Моргана Δⁿ равно числу отображений f мно‐

жества A из k элементов на множество B из n элементов, т. е. таких ото‐

бражений, что f(A) = f(B); число Белла B_n есть число разл. разбиений множества из n элементов на непересекающиеся подмножества.
При исследовании свойств комбинаторных чисел широко используют производящиефункции, рекуррентныесоотношенияи конечно-разностные уравнения. Во многих случаях на рассматриваемом множестве объектов удаётся построить подходящую вероятностную модель и тем самым ком‐ бинаторную задачу перечислительного характера сформулировать как задачу изучения распределения вероятностей соответствующей случай‐ ной величины. Такая интерпретация даёт возможность применять при изучении комбинаторных чисел разл. методы теории вероятностей.


N
Под комбинаторными многочленами понимают производящие функции комбинаторных чисел или производящие функции этих чисел с некото‐ ^{рыми весами. Напр., производящей функцией чисел сочетаний} C^{k ,}

k = 0, 1, . . . , N, является бином Ньютона
N


N
∑ C^k x^k = (1 + x)^N ;

k=0
для чисел Стирлинга
n

∑ S(n, k)x^k = x(x − 1) … (x − n + 1),

k=0

n

∑ σ(n, k)x_k = xⁿ,

k=0
где (x)_k = x(x − 1) … (x − k + 1), k = 0, 1, … , n.

Библиография

Оставьте ваш e-mail, чтобы получать наши новости

О проекте Контакты

Купить книжную версию

ВашEmail