Файл: Методы кодирования данных (Основные понятия теории кодирования).pdf
Добавлен: 14.03.2024
Просмотров: 34
Скачиваний: 0
СОДЕРЖАНИЕ
1. Основные понятия теории кодирования
2. Способы кодирования: классификация
2.1. В соответствии с условием построения кодовых комбинаций
2.2. В соответствии с количеством уникальных символов
2.3. В соответствии с формой представления
2.4. В соответствии с возможностями обнаружения/исправления ошибок
2.5. В соответствии с количеством одновременно кодируемых символов
3. Методы кодирования: классификация
3. Методы кодирования: классификация
3.1. Коды префиксные
Под префиксом традиционно принято понимать приставку. В теории кодирования префиксным кодом является код переменной длины, который удовлетворяет условию Роберта Фано: неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с префиксом какого-либо другого, более длинного кода.
Так, например, если один из символов алфавита имеет код «101», то в качестве других кодов не могут быть использованы последовательности «1» и «10», но можно использовать «0» и «11».
Декодирование таких слов выполняется однозначно слева направо. Сопоставление с таблицей при этом всегда дает точное указание конца одного кода и начало другого, что позволяет избавиться от использования разделителей.
Одним из примеров префиксных кодов является код Шеннона-Фано. Алгоритм данного метода использует избыточность сообщения, которая заключается в неоднородном распределении частот символов первичного алфавита. Другими словами, коды более частых символов заменяются короткими двоичными последовательностями, а коды редко встречающихся символов – более длинными.
Другой пример – код Хаффмана, являющийся оптимальным префиксным кодом для дискретных источников без памяти. Алгоритм данного метода состоит из двух этапов:
- первый этап – первичный алфавит на каждом шаге сокращается на один символ. На следующем шаге рассматривается уже новый первичный алфавит. Соответственно, количество шагов на две единицы меньше количества символов исходного алфавита;
- второй этап – пошаговое формирование кода символов. Заполнение кода при этом осуществляется с символов последнего сокращенного первичного алфавита.
3.2. Коды арифметические
Алгоритмы арифметического кодирования обеспечивают практически оптимальную степень сжатия сообщения с точки зрения энтропийной оценки Шеннона. Данные методы позволяют упаковывать символы первичного алфавита без потерь при условии, что известно распределение частот этих символов.
Наиболее простым методом является унарный код, сопоставляющий некоторому числу i двоичную комбинацию вида 1i0. Запись вида 0 или 1 означает соответственно серию из m нулей или единиц. Например, унарными кодами чисел 1, 2, и 3 являются последовательности unar(1)=10, unar(2)=110 и unar(3)=1110 соответственно.
Еще одним примером арифметических кодов являются коды Фибоначчи. Числа Фибоначчи – элементы числовой последовательности:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, …,
в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи) [12].
Данное кодирование предполагает разложение исходного числа n в сумму чисел Фибоначчи fi (f1 = 1; f2 = 2; fi = fi-1 + fi-2). Любое натуральное число может быть однозначно представлено в виде суммы чисел Фибоначчи. Следовательно, можно построить код числа как последовательность битов, каждый из которых указывает факт наличия в n определенного числа Фибоначчи. Кроме того, если в разложении числа n присутствует fi, то в этом разложении не может быть числа fi+1. Следовательно, логично для конца кода использовать дополнительную единицу. Это значит, что две идущие подряд единицы будут означать окончание кодирования текущего числа. Примеры кода Фибоначчи приведены в таблице 1 [8].
Таблица 1 – Примеры кода Фибоначчи
|
n \ fi |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
31 |
|
1 |
1 |
(1) |
||||||
|
2 |
0 |
1 |
(1) |
|||||
|
3 |
0 |
0 |
1 |
(1) |
||||
|
4 |
1 |
0 |
1 |
(1) |
||||
|
5 |
0 |
0 |
0 |
1 |
(1) |
|||
|
6 |
1 |
0 |
0 |
1 |
(1) |
|||
|
7 |
0 |
1 |
0 |
1 |
(1) |
|||
|
8 |
0 |
0 |
0 |
0 |
1 |
(1) |
||
|
… |
… |
… |
… |
… |
… |
… |
||
|
12 |
1 |
0 |
1 |
0 |
1 |
(1) |
||
|
13 |
0 |
0 |
0 |
0 |
0 |
0 |
(1) |
|
|
… |
… |
… |
… |
… |
… |
… |
… |
|
|
20 |
0 |
1 |
0 |
1 |
0 |
1 |
(1) |
|
|
21 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
(1) |
Последовательность символов, при сжатии методом арифметического кодирования рассматривается как некоторая двоичная дробь из интервала [0, 1). Результат сжатия представляется как последовательность двоичных цифр из записи этой дроби.
Опишем алгоритм построения этого кода. Пусть у нас есть некий первичный алфавит, состоящий из трех символов: A = {a, b, !}, а также данные о вероятности использования символов P = {0,3; 0,6; 0,1}. Последний символ рассматриваемого алфавита («!») не несет информационной нагрузки, а лишь является признаком окончания сообщения. Он требуется декодировщику для однозначного декодирования полученного сообщения. На практике вероятность его использования берут заведомо малой. Данный символ можно не использовать только в том случае, когда декодировщику точно известна длина кодируемого сообщения.
Существует особый адаптивный алгоритм, позволяющий реализовать метод арифметического кодирования. Данный алгоритм при каждом сопоставлении символу кода, меняет внутренний ход вычислений таким образом, что в следующий раз этому же символу может быть сопоставлен другой код. Другими словами, происходит адаптация алгоритма к символам, поступающим для кодирования.
При декодировании происходит аналогичный процесс. Необходимость применения адаптивного алгоритма возникает в том случае, когда до начала работы алгоритма вероятностные оценки для символов сообщения неизвестны.
3.3. Коды цифровые
Одним из наиболее ярких примеров цифровых кодов является двоично-десятичный код. Основная система счисления здесь десятичная, но каждая значащая цифра представляется в виде четырех двоичных знаков и содержит десять значений сигнала от 0 до 9. В таблице 2 представлено изображение двоично-десятичных кодов с различными весами разрядов.
Как видно из таблицы, практически все двоично-десятичные коды не имеют однозначности в отображении. Исключением является код с весами 8‑4‑2-1.
Двоично-десятичные коды нашли широкое применение в аналого-цифровых преобразователях. Каждая значимая десятичная цифра в таком коде представляется четырьмя двоичными знаками и содержит десять значений сигнала от нуля до девяти.
Код 8-4-2-1 позволяет осуществлять арифметические операции с использованием двоично-десятичных сумматоров, которые проектируются как обычные двоичные сумматоры с добавлением устройств формирования дополнительных переносов, которые требуются в тех случаях, когда сумма двух двоично-десятичных чисел становится больше или равна десяти [5].
Таблица 2 – Двоично-десятичное представление
|
Десятичный код |
Двоично-десятичный код |
||
|
8-4-2-1 |
2-4-2-1 |
5-1-2-1 |
|
|
0 |
0000_0000 |
0000_0000 |
0000_0000 |
|
1 |
0000_0001 |
0000_0001 |
0000_0001 или 0000_0100 |
|
2 |
0000_0010 |
0000_0010 или 0000_1000 |
0000_0010 или 0000_0101 |
|
3 |
0000_0011 |
0000_0011 или 0000_1001 |
0000_0011 или 0000_0110 |
|
4 |
0000_0100 |
0000_0100 или 0000_1010 |
0000_0111 |
|
5 |
0000_0101 |
0000_0101 или 0000_1011 |
0000_1000 |
|
6 |
0000_0110 |
0000_0110 или 0000_1100 |
0000_1001 или 0000_1100 |
|
7 |
0000_0111 |
0000_0111 или 0000_1101 |
0000_1101 или 0000_1010 |
|
8 |
0000_1000 |
0000_1110 |
0000_1110 или 0000_1011 |
|
9 |
0000_1001 |
0000_1111 |
0000_1111 |
Еще одним примером цифровых кодов является циклический код Грея. Характерная особенность данного кода – изменение только одной позиции при переходе от одной кодовой комбинации к другой. Данное свойство широко применяется как для построения некоторых типов аналого-цифровых преобразователей, так и для повышения надежности преобразователей при помощи самоконтроля и резервирования.
Для того чтобы перейти от натурального двоичного кода к коду Грея, необходимо соблюдать следующие правила:
- если в предыдущем разряде двоичного кода стоит 0, то в данном разряде цифра сохраняется;
- если в предыдущем разряде двоичного кода стоит 1, то данном разряде цифра меняется на противоположную.
Такое представление приведено в таблице 3.
Таблица 3 – Цифровой код Грея
|
А10 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
А2 |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
|
АГр |
0000 |
0001 |
0011 |
0010 |
0110 |
0111 |
0101 |
0100 |
|
А10 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
А2 |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
|
АГр |
1100 |
1101 |
1111 |
1110 |
1010 |
1011 |
1001 |
1000 |
Главной трудностью применения кода Грея является непостоянство весов разрядов, а также изменение их знаков.
Чтобы перейти от кода Грея к натуральному числу, необходимо воспользоваться следующим правилом: если слева от данной цифры находится четное число единиц, то цифра сохраняется, в противном случае меняется на противоположную.
4. Обзор методов помехоустойчивого кодирования
В процессе передачи информации по цифровым каналам она подвергается кодированию. Существует особый американский стандарт ASCII, который в соответствие каждой букве алфавита ставит определенное шестнадцатеричное число. Таблица кодов ASCII приведена на рисунке 1.

Рисунок 1 – Таблица кодов ASCII
Глядя на эту таблицу, можно сделать вывод, что для передачи одной буквы, она должна быть заменена соответствующей кодой комбинацией из семи разрядов. Любая двоичная комбинация из семи разрядов определяет какой-то знак алфавита. Если в процессе передачи произойдет хотя бы одна ошибка, символ будет распознан неверно.
В основе идеи помехоустойчивого кодирования лежит добавление лишних символов к сообщению, которые помогают обнаружить ошибку. Таким образом, множество кодовых комбинаций разбивается на два:
- множество разрешенных комбинаций;
- множество запрещенных комбинаций.
Если в результате ошибки исходная комбинация перешла в множество запрещенных, то ошибку можно обнаружить. Однако, возможно, что совокупность ошибок переведет передаваемую кодовую комбинацию в другую разрешенную. Тогда вместо одной буквы мы получим другую букву, и ошибка не будет обнаружена.
Чтобы иметь возможность вовремя находить и исправлять ошибки, разрешенная комбинация должна как можно больше отличаться от запрещенной. Количество разрядов, которыми отличаются две соседние комбинации называется расстоянием. Вес комбинации – число единиц в ее записи.
Рассмотрим исправление ошибок на примере комбинаций 000 и 111 (см. рисунок 2). Расстояние между этими комбинациями d = 3. Следовательно, любые единичные ошибки в этих комбинациях остаются в области t ≤ 1. Другими словами, области не пересекаются и ошибки могут быть исправлены.
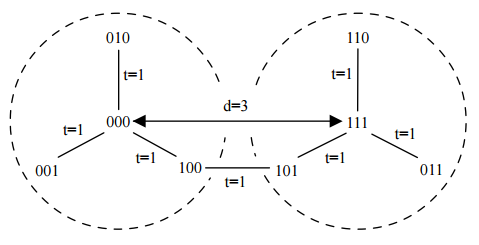
Рисунок 2 – Пример исправления ошибок


