Файл: Первое высшее техническое.docx

^{Лаборатория механики} Лабораторная работа № 6 01.09.2022
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ



МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»

Кафедра общей и технической физики
ОТЧЁТ

ПО ЛАБОРАТОРНОЙ РАБОТЕ №6

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА

Выполнил:

Дата выполнения:

Проверил:

Дата защиты:

САНКТ-ПЕТЕРБУРГ

2022

1. ЦЕЛЬ РАБОТЫ

Исследовать зависимость момента инерции крестовины с надетыми на нее грузиками от распределения массы относительно оси вращения, проходящей через центр масс крестовины.

2. КРАТКОЕ ТЕОРЕТИЧЕСКОЕ СОДЕРЖАНИЕ

Явление, изучаемое в работе. Зависимость момента инерции от распределения массы относительно оси вращения.

Определения физических понятий, объектов, процессов и величин.

Поступательное движение – называется такое движение, при котором любая прямая, мысленно проведенная в теле, остается постоянной самой себе в течение всего времени движения. При поступательном движении траектории всех точек тела одинаковы, скорости и ускорения всех точек в данный момент времени равны. Поэтому можно описывать движение одной точки.

Вращательное движение – такое движение, при котором все точки тела движутся по окружностям

---

, центры которых лежат на одной прямой, называемой осью вращения, а плоскости перпендикулярны к ней.

Момент инерции тела – скалярная физическая величина, является мерой инертности тела при вращательном движении. Момент инерции тела зависит от размеров и формы тел и от распределения массы тела относительно оси вращения.

Момент силы – векторная физическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы, на вектор этой силы.

Маятник Обербека – лабораторное устройство для изучения законов динамики вращательного движения.

Законы и соотношения, описывающие изучаемые процессы, на основании которых получены расчетные формулы. Пояснения к физическим величинам и их единицам измерения.

Второй закон Ньютона для поступательного движения тела (m = const):



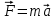
где 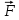- сумма всех внешних сил, приложенных к телу [Н]; m – масса тела [кг]; a 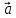- линейное ускорение [м/с²].

Основной закон динамики вращательного движения твердого тела:



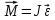
где 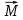- суммарный момент внешних сил [Н·м], приложенных к телу относительно оси вращения; J - момент инерции тела относительно той же оси [кг·м²]; 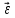- угловое ускорение [рад/с²].

Момент инерции материальной точки [кг·м²]:



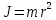
где m – масса точки [кг]; r – расстояние до оси вращения [м].

Момент инерции сплошного твёрдого тела определяется по формуле:



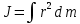
где r - расстояние [м] от элемента с массой dm [кг] до оси вращения.

Момент силы относительно точки О это вектор, определяемый как векторное произведение радиус-вектора и силы:



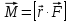
где 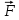- сила, 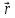- радиус-вектор, проведенный из точки

---

О, в точку приложения силы.

В маятнике Обербека на груз действует сила тяжести 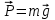и сила натяжения 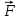. В соответствии со вторым законом Ньютона можно записать: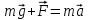



где g - ускорение свободного падения [м/с²]; а – величина линейного ускорения, с которым движется груз [м/с²].

Крестовина приходит во вращательное движение под действием момента силы натяжения:



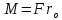
где 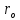- радиус шкива [м].

Используя соотношение между угловым и линейным ускорением 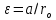, получим выражение для момента инерции: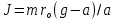



3. СХЕМА УСТАНОВКИ

1. 
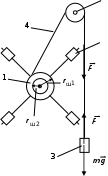   Крестовина диаметром d;
   
2. 
   Грузы массами m’;
   
   
   2
   
   
3. 
   Груз массой m;
   
4. 
   Нерастяжимая нить;
   
5. 
   Неподвижный блок.
   

4. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ

Расчётная формула для момента инерции крестовины с грузами:



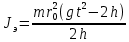
где m - масса груза [кг]; g - ускорение свободного падения [м/с²]; 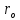- радиус шкива [м]; h - расстояние, пройденное грузом [м]; t - время спуска [с].

Из теоретических соображений следует, что момент инерции крестовины с четырьмя грузами массой m’ (если считать грузы материальными точками), можно выразить формулой:



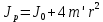
где 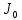- момент инерции тела [кг·м²] при r = 0.

Из этой формулы следует, что 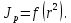Следовательно, если построить график этой функции в координатах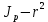

---

, то должна получиться прямая, продолжение которой будет пересекать ось ординат в некоторой точке, соответствующей 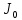. Такое построение можно было бы сделать приближенно, «на глаз». Однако математические методы обработки результатов наблюдения позволяют сделать такое построение достаточно точным. Наиболее просто это можно сделать, с помощью метода наименьших квадратов, вычислив 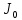и m .

Для этого перепишем формулу в виде:



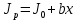
где 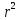= х и 4m' = b.

Метод наименьших квадратов позволяет найти коэффициенты уравнения 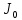и 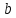, используя формулы: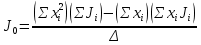





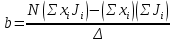
Здесь 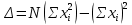; N - число опытов; 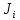- экспериментальные значения момента инерции 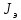, полученные для каждого опыта.

5. ФОРМУЛЫ ДЛЯ РАСЧЕТА ПОГРЕШНОСТЕЙ КОСВЕННЫХ ИЗМЕРЕНИЙ

Формулы для расчета погрешностей косвенных измерений:

Средняя квадратическая погрешность косвенных измерений J_э:



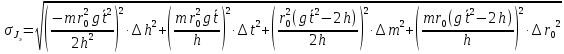
где Δh, Δt, Δm, Δr₀ - среднеквадратические (и абсолютные) погрешности прямых измерений пути груза [м], времени спуска [с], массы груза [кг] и радиуса шкива [м] соответственно; m - масса груза [кг]; g - ускорение свободного падения [м/с²] ; r₀ - радиус шкива [м]; h - путь груза [м]; 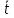- среднее время спуска [с].

Дисперсия результата измерения момента инерции:



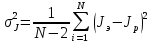
где N - количество опытов;

---

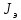
– экспериментальное значение момента инерции [кг·м²]; 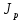– теоретическое значение момента инерции [кг·м²].

6. РАСЧЕТНАЯ ЧАСТЬ

Таблица 1

Физическая величина	r	t	̅t	Jэ	Jp
Ед. изм. Номер опыта	м	с	с	кг·м2	кг·м2
1	0,22	4,914	4,839	0,0491	0,0485
		4,803
		4,8
2	0,195	4,441	4,308	0,0389	0,0387
		4,233
		4,249
3	0,18	3,996	3,969	0,033	0,0334
		3,906
		4,005
4	0,165	3,592	3,607	0,0272	0,0285
		3,637
		3,593
5	0,15	3,365	3,416	0,0244	0,0240
		3,401
		3,481
6	0,135	3,129	3,08	0,0198	0,0199
		3,059
		3,052
7	0,12	2,904	2,87	0,0171	0,0163
		2,869
		2,838

Таблица 2

Физическая величина	ri	xi	Ji		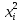xi Ji
Ед. изм. Номер опыта	м	м2	кг·м2	м4	кг·м4
1	0,22	0,0484	0,0491	0,002343	0,002376
2	0,195	0,0380	0,0389	0,001444	0,001478
3	0,18	0,0324	0,033	0,001050	0,001069
4	0,165	0,0272	0,0272	0,000740	0,000740
5	0,15	0,0225	0,0244	0,000506	0,000549
6	0,135	0,0182	0,0198	0,000331	0,000360
7	0,12	0,0144	0,0171	0,000207	0,000246
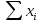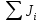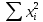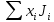		0,2011	0,2095	0,006621	0,006818

---