Файл: Цель работы изучение изопроцессов в газах определение показателя адиабаты методом КлеманаДезорма.doc

Цель работы: изучение изопроцессов в газах; определение показа­теля адиабаты методом Клемана-Дезорма.

Основные понятия

Газ - агрегатное состояние вещества, в котором составляющие его атомы и молекулы беспорядочно движутся. Энергия этого движения назы­вается внутренней энергией. Величина внутренней энергии тела складыва­ется из кинетической энергии хаотического движения молекул и потенци­альной энергии их взаимного расположения: . К реально­му газу при не слишком низких температурах и достаточно малых давлениях применима модель идеального газа. Согласно этой модели молекулы можно рассматривать как невзаимодействующие материальные точки (Е_ВЗ ⁼ 0), при столкновениях такие молекулы ведут себя как абсолютно упругие шарики.

Внутренняя энергия газа определяется его абсолютной температурой Т и числом степеней свободы молекул газа i . Числом степеней свободы i движения механической системы называется число независимых коорди­нат, определяющих её положение в пространстве. Применяя это понятие к идеальному одноатомному газу, получим, что его частицы имеют три сте­пени свободы поступательного движения (i ⁼ 3). Многоатомные молеку­лы (сложные частицы) кроме поступательных обладают ещё вращательны­ми и колебательными степенями свободы. Рассмотрим сложную частицу, состоящую из двух точечных частиц: между ними возможны два типа свя­зи. Первый тип - точечные частицы жестко связаны между собой и ведут себя наподобие жесткой гантели. В этом случае сложная частица имеет пять степеней свободы - три поступательные и две вращательные. Второй тип - связь между частицами не жесткая, и они могут совершать колеба­тельные движения вдоль соединяющей их линии. В этом случае добавля­ются ещё две степени свободы на кинетическую и потенциальную энергию колебаний.

В соответствии с законом равномерною распределения энергии по степеням свободы (закон Больцмана) на каждую из них приходится энер­гия, равная . Здесь - постоянная Больцмана.

Один моль любого газа содержит число молекул

---

, равное числу Авогадро, и обладает полной энергией , где R ⁼ kN_А - газовая постоянная, R ⁼ 8,3 1 Дж/(моль*К). N_A = 6,02*10^-23 моль^-1. Внутренняя энергия идеального газа массой m:

(1)

где - число молей, μ - молярная масса.

В термодинамике состояние газа характеризуется объемом V , давле­нием Р и температурой Т . Параметры Р, V, Т связаны друг с другом функциональной зависимостью, называемой уравнением состояния. Для

идеального газа - уравнение Менделеева - Клапейрона. Для одного моля идеального газа PV=RT. Равновесным называется состоя­ние газа, при котором значения параметров Р, V и Т постоянно во време­ни, причем давление и температура имеют постоянные значения со всех частях объема. Равновесное состояние изображают точкой на P-V, T-V или Р-Т диаграммах, которые представляют собой графическо*е изображе­ние соотношений между параметрами Р, V и Т.

Процесс описывается изменением во времени параметров системы. Процесс, состоящий из бесконечно близких равновесных состояний, назы­вается равновесным и может быть изображен на диаграмме в виде непре­рывных кривых. Процесс, при котором один из параметров остается неиз­менным, называется изопроцессом.

В идеальном газе можно осуществить три изопроцесса:

1) при постоянном объеме V = const - изохорический 2) при постоянном давлении Р = const - изобарический 3) при постоянной температуре Т = const - изотермический . На рис. 1 представлены эти зависимости в координатах Р, V. Существует две формы переда­чи энергии от одних тел к другим: в форме работы А и в форме теплоты Q. Энергия механического движения может превращаться в энергию теп­лового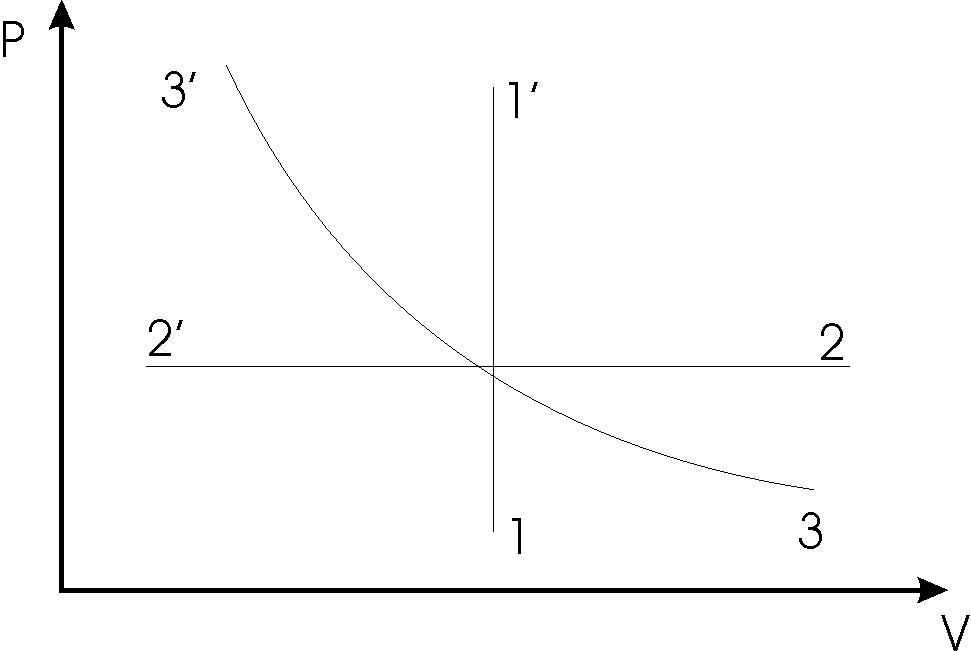

рис. 1

---

движения и наоборот. При этих превращениях должен выполняться закон сохранения и превра­щения энергии. Применительно к термодинамическим процессам таким законом является первое начало термодинамики: теплота, сообщаемая сис­теме, расходуется на увеличение её внутренней энергии и на совершение ею работы против внешних сил. При малом изменении состояния системы:

(2)

Отличия и записи δQ, dU и δА выражают характерные физические различия этих величин. Если внутренняя энергия является однозначной функцией состояния термодинамической системы, то понятия теплоты и работы имеют смысл только в связи с процессом изменения состояния сис­темы. При совершении произвольного процесса, в результате которого она возвращается в исходное состояние, полное изменение внутренней энергии равно нулю , в то время как могут быть и не рав­ны нулю (например, в цикле Карно).

При сообщении системе теплоты δQ её температура изменяется на dT. Величина, равная отношению δQ к dT, называется теплоемкостью тела. Теплоемкость измеряется количеством теплоты, которое надо сооб­щить телу для повышения его температуры на один Кельвин. Теплоемкость, отнесенная к единице массы тела, называется удельной: . Теплоемкость моля вещества называется молярной:

(3)

Теплоемкость в общем случае не характеризует свойства тела, по­скольку она является характеристикой как тела, так и условий нагревания, поэтому она не имеет определенного значения. Она приобретает опреде­ленные значения, если фиксировать условия нагревания, тогда она являет­ся характеристикой тела. Наиболее важными являются теплоемкости для случаев, когда теплота передается газу при постоянном давлении (С

---

_P) и постоянном объеме (С_V).

В изохорическом процессе объем не изменяется, газ не совершает ра­боту против внешних сил, поэтому сообщаемое газу извне количество теп­ла δQ расходуется на изменение внутренней энергии: δQ ⁼ dU. Тепло­емкость одного моля газа на основании (2):

(4)

В изобарическом процессе тепло δQ расходуется на увеличение внут­ренней энергии и на совершение газом работы прочив внешних сил δА: , причем . Поэтому , откуда
(5)

Соотношение называется уравнением Майера.

При рассмотрении термодинамических процессов важно знать харак­терное для каждого газа отношение С_P к С_V, называемое показателем адиабаты γ. В соответствии с (1), (4), (5):

(6)

Общее уравнение адиабатического процесса получают из первого на­чала термодинамики, полагая δQ ⁼ 0 (теплоизолированность). Соотно­шение (2) в случае адиабатного процесса:
(7)

или

CvdT + PdV = 0 (8)

Разделив (8) на С_VТ, получим

(9)

Проинтегрируем, затем пропотенцируем выражение (9) и получим:

(10)

Это уравнение адиабаты в переменных Т, V. Воспольззовавшись уравнением Менделеева-Клайперона для

1 моля газа PV= RT , получим уравнение адиабаты в переменных Р, V:

(11)

Результаты эксперимента

№
1 2 3 4 5 6 7	h1= 25.5-8= 17.5 h1= 25.3-8.2= 17.1 h1= 26.1-7.2= 18.9 h1= 24-9.3= 14.7 h1= 25.1-8.3= 16.8 h1= 24.9-8.5= 16.4 h1= 28-5.3= 22.7		h2= 18.5-14.5= 4 h2= 18.4-14.8= 3.6 h2= 18.7-14.5= 4.2 h2= 18.1-15.1= 3 h2= 18.6-14.4= 4.2 h2= 18.2-15= 3.2 h2= 19-14.1= 4.9
1 2 3 4		5 6 7

---

Обработка результатов эксперимента

Найдем среднее значение :



Найдем кол-во молей газа в баллоне:



Найдем внутреннюю энергию газа в баллоне:



По данным исходного состояния и значению  вычислим:








Погрешности

Погрешность вычисления показателя адиабаты :

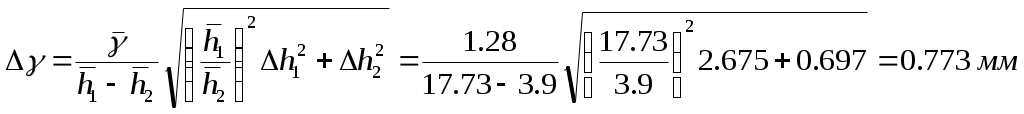
где h₁ и h₂ определяются по формулам:



Погрешность в значении γ определяем по формуле:


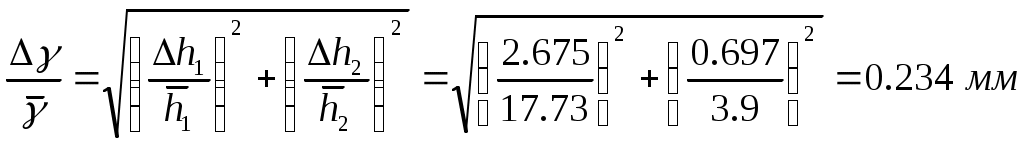
Вывод

В результате проведения лабораторной работы изучили изопрцессы в газах.

Определили значение γ = 1,28

количество молей газа в баллоне ν = 0,4 моль

внутреннюю энергию газа U₀ = 2500 Дж

по данным исходного состояния P₁ = 277300 Па

V₁ = 0,005 м³

T₁ = 418,17 К

Е = 3475 Дж.

---