Файл: Л. Н. Гумилев атындаы еуразия лтты университеті апаратты технологиялар факультеті Кафедра.docx

Л.Н.ГУМИЛЕВ АТЫНДАҒЫ ЕУРАЗИЯ ҰЛТТЫҚ УНИВЕРСИТЕТІ

Ақпараттық технологиялар факультеті

Кафедра: Ақпараттық қауіпсіздік

Пән: Сигналдарды жіберу теориясы

ЕСЕП

ЛАБОРАТОРИЯЛЫҚ ЖҰМЫС №1

ТАҚЫРЫБЫ: «Matlab компьютерлік математика жүйесінің интерфейсін зерттеу»

Орындаған: Темирова Шырын

Тексерген: Онгарбаева А.И.

Топ: АҚЖ 43

Астана қ, 2022 ж.

МАЗМҰНЫ

Зертханалық жұмыс 1

КОМПЬЮТЕР МАТЕМАТИКАНЫҢ ЖҮЙЕСІНІҢ ИНТЕРФЕЙСІН ЗЕРТТЕУ

ПРИМЕР 1



ПРИМЕР 2



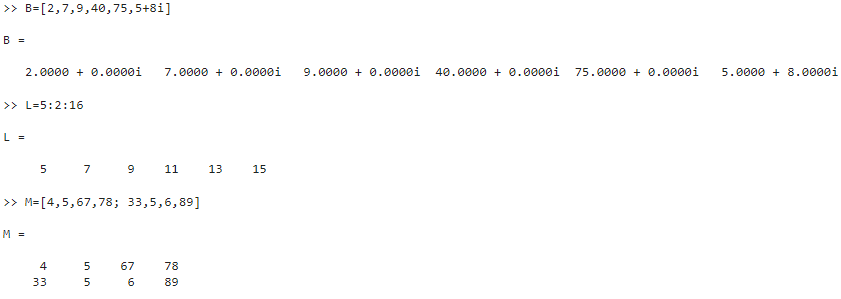
Бұл мысалда екінші жол келесі деректерді құрайды: 5-массивтің басы, 2-көрші элементтердің мәндерінің айырмашылығы, 16 саны-массивтің жоғарғы шекарасы.

Үшінші жол екі жолдан және төрт бағаннан тұратын екі өлшемді массив құрайды:



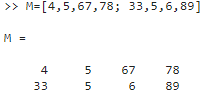
Бір өлшемді массив элементтерінің саны length функция арқылы анықталады.



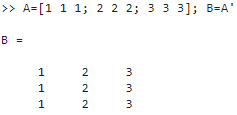
Бұл мысалда біз матрица жолдарын оның бағандарымен ауыстырдық, оны ауыстыруға болады, ол «’» белгісімен көрсетіледі
* белгісі сызықтық алгебра мағынасында матрицалар мен векторлардың көбейтіндісіне қойылады. Операция тек нөмір болғанда ғана орындалады

сол жақ операндтағы бағандар оң жақтағы жолдар санына тең:



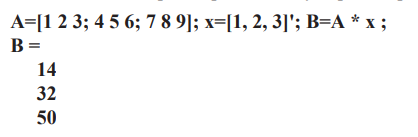
Бірдей өлшемдегі массивтерді элементтік көбейту және бөлу үшін екі таңбаның тіркесімімен белгіленетін амалдар қолданылады: .* және ./. ./ операциясынан басқа .\ операциясы да бар. A./B өрнегі A(k,m)/B(k,m) элементтері бар матрицаға, ал A.\B өрнегі B(k,m)/A(k,) элементтері бар матрицаға әкеледі. м).

---

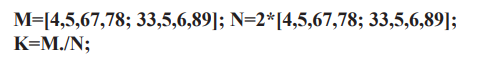
Баған элементтерінің қосындысы мен орташа мәнін анықтау

матрицалар сәйкес функциялар қолданылады: қосынды(х), орта(x).

Зертханалық жұмыс 2

ДЫБЫСТЫҚ ФАЙЛДАР БОЙЫНША ОПЕРАЦИЯЛАР.

Жұмыстың мақсаты. Массивтермен және файлдармен жұмыс істеу тәсілдерін зерттеу, а

сондай-ақ, жұмыс нәтижелерін визуализациялау құралдары.

Тапсырма 1. Төменде келтірілген материалды зерттеп, мәтінде келтірілген шаралар мен жаттығуларды қайталаңыз

Екі өлшемді график

Гармоникалық дірілге сәйкес келетін функцияның графигін құрайық

y= A * sin (2*pi * F * t+alfa), мұндағы скалярлық айнымалылар A, F, alfa

сәйкесінше амплитудасын, жиілігін және фазасын (радианмен) анықтаңыз. Pi айнымалысы π санын анықтайды. T айнымалысы-тербеліс уақытының аралығын белгілейтін бір өлшемді массив. Келесі сандық деректермен массивті y анықтаймыз:

A=2;

F=100;

alfa=pi/4;

Fd=1000;

t=0:1/Fd:0.05;

Мұнда t массиві нөлден 0,05 с-қа дейінгі уақыт аралығын кезеңмен белгілейді

1/Fd іріктеу, (FD – гармоникалық тербелісті іріктеу жиілігі). Біз массивті есептейміз және plot(t, y) функциясын қолдана отырып, оларға гармоникалық тербеліс графигін саламыз

y=a * sin(2*pi * F * t+alfa);

plot (t, y)



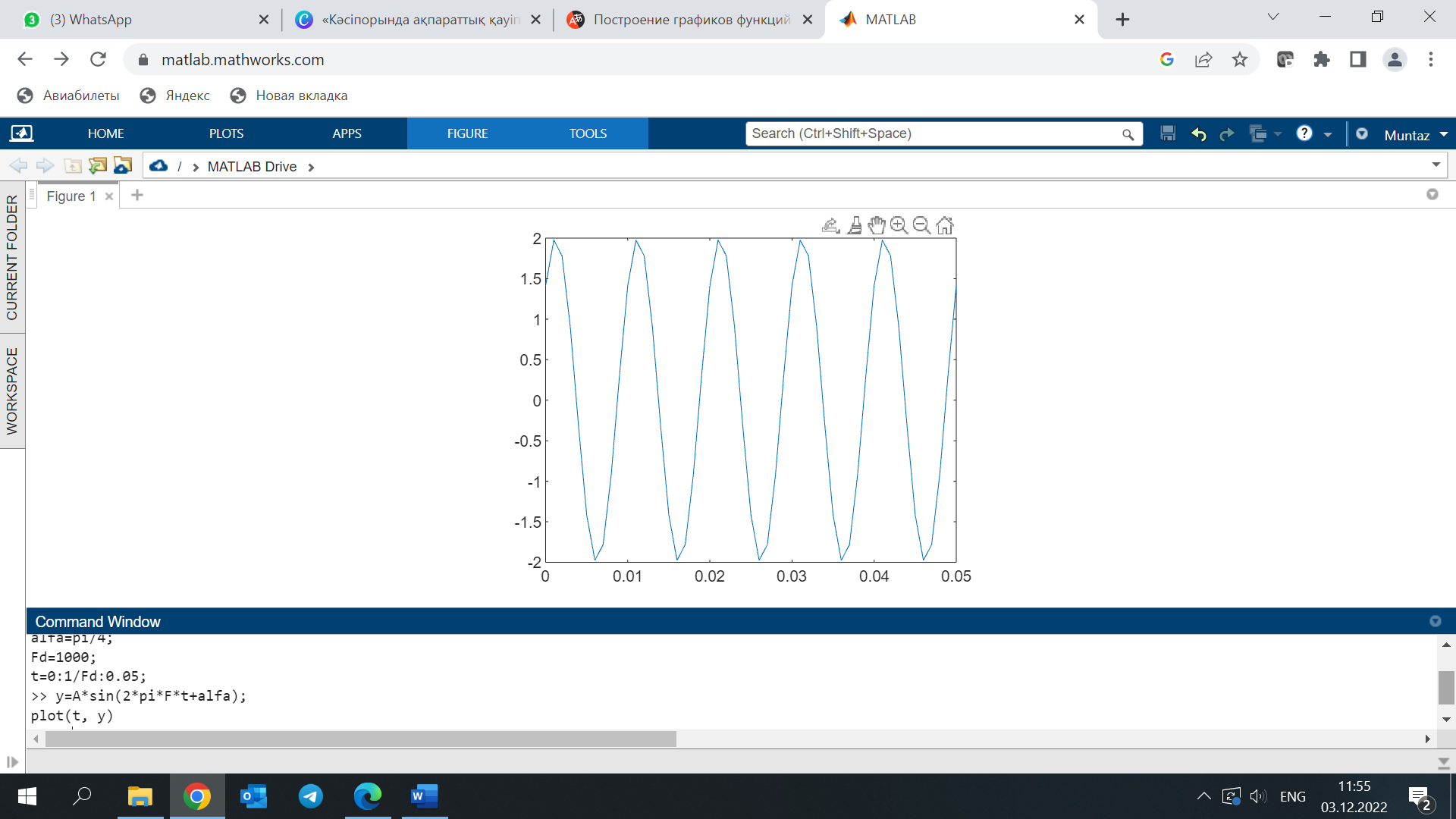
Графикті неғұрлым ыңғайлы талдау үшін оған grid функциясының қуаты бар торды қолданамыз (grid on-графикке тор салады, grid off – оның тазартады)

grid on

Plot(t,y) функциясы келесідей график жасайды: нәтижелер есептеулер - графиктегі нүктелер-түзу сызықтармен қосылады, яғни графикті құру кезінде сызықтық интерполяция қолданылады. Графикалық нысандар арнайы нысандарда көрсетіледі мәзірі бар графикалық терезелер және түймелері бар жеке құралдар тақтасы.

Дисплей экранынан бірінші графикалық терезені алып тастамай, пернетақта класынан келесі өрнектерді енгізіңіз:

z =A*cos(2*pi*F*t+alfa);

plot(t, z)



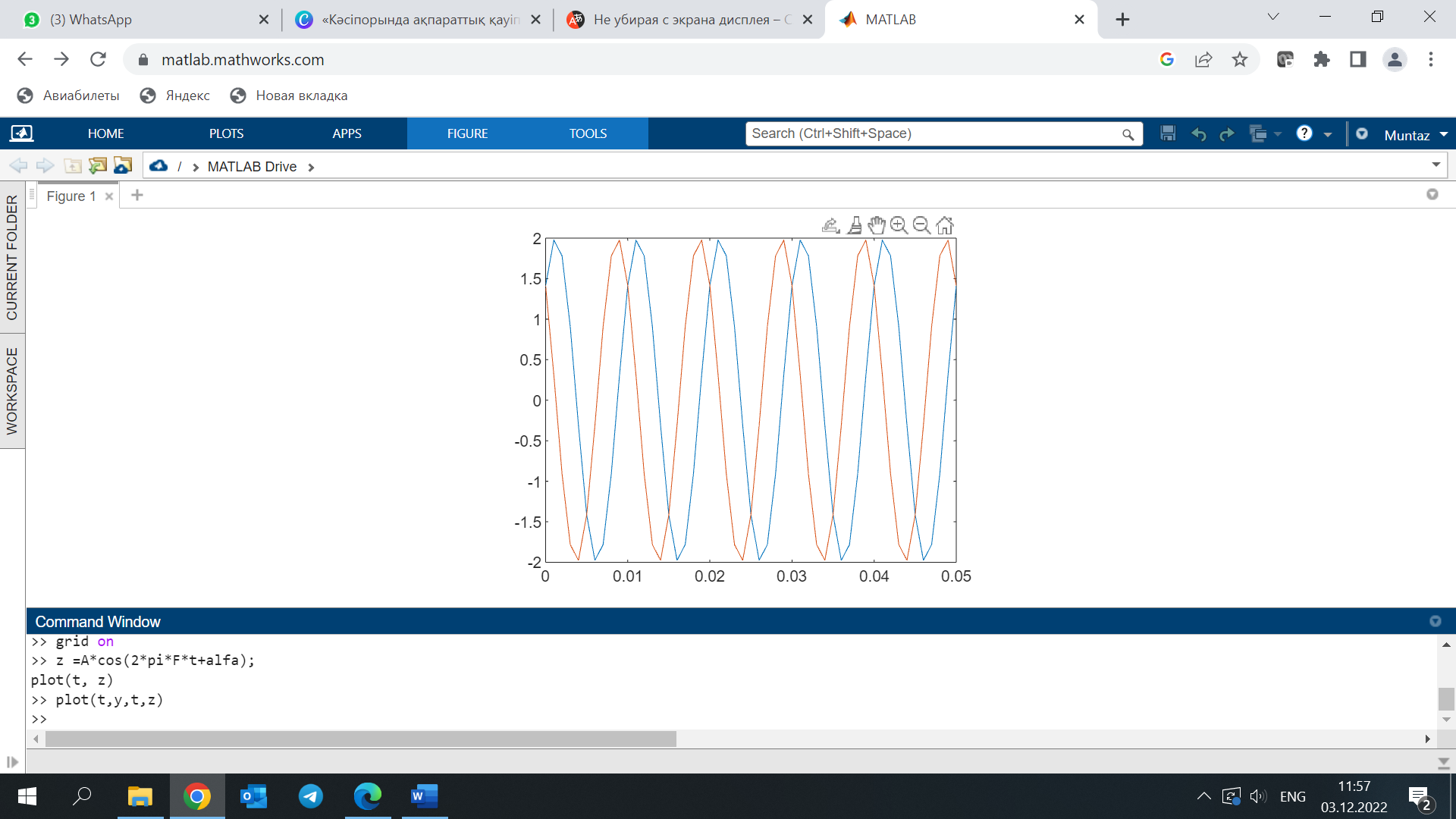
Разноцветные полосы получили

Егер графиктерді әр түрлі терезелерге орналастыру қажет болса, онда жаңа терезе жасайтын figure командасы қолданылады.

у=A*sin(2*pi*F*t+alfa);

---

plot(t, у)

figure z=A*cos(2*pi*F*t+alfa);

plot(t, z)



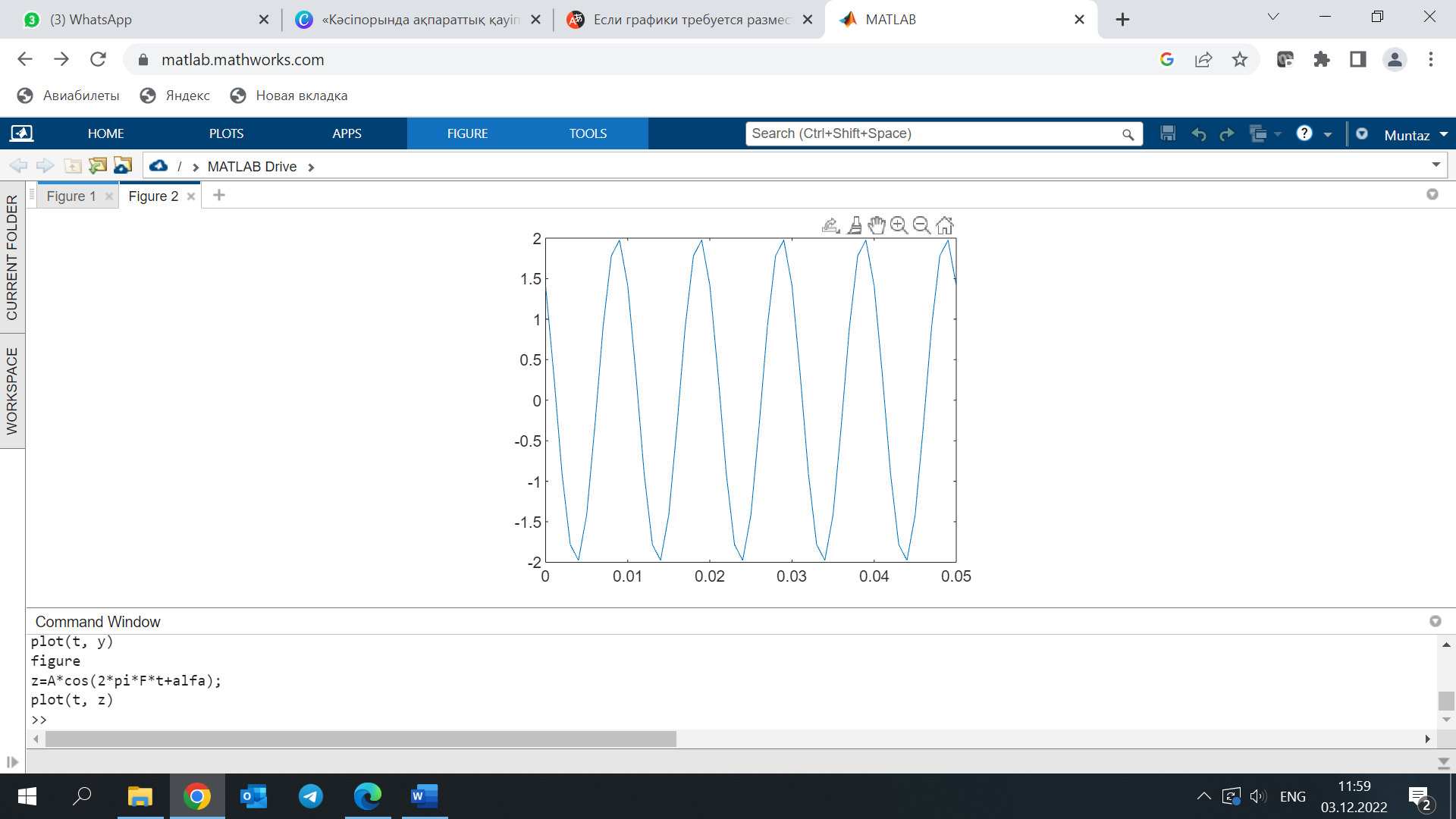
Subplot функциясы графикалық Шығыс аймағын бөлуге мүмкіндік береді бірнеше ішкі салаларға арналған ақпарат, олардың әрқайсысында сіз әр түрлі функциялардың графиктерін шығарыңыз. Subplot функциясы үшеуін қабылдайды сандық аргументтер, олардың біріншісі подбла стей серияларының санына тең, екіншісі – ішкі аймақ бағандарының санына, ал үшінші аргумент-ішкі аймақ нөмірі (нөмір жаңасына көшу арқылы жолдар бойымен есептеледі қатардың соңына жету үшін қатар)

Егер графикте тек нүктелерді көрсету қажет болса-есептеу нәтижелері, онда stem(x,y) командасын пайдалану ыңғайлы, оның көмегімен"сабақ" графигі салынуда.



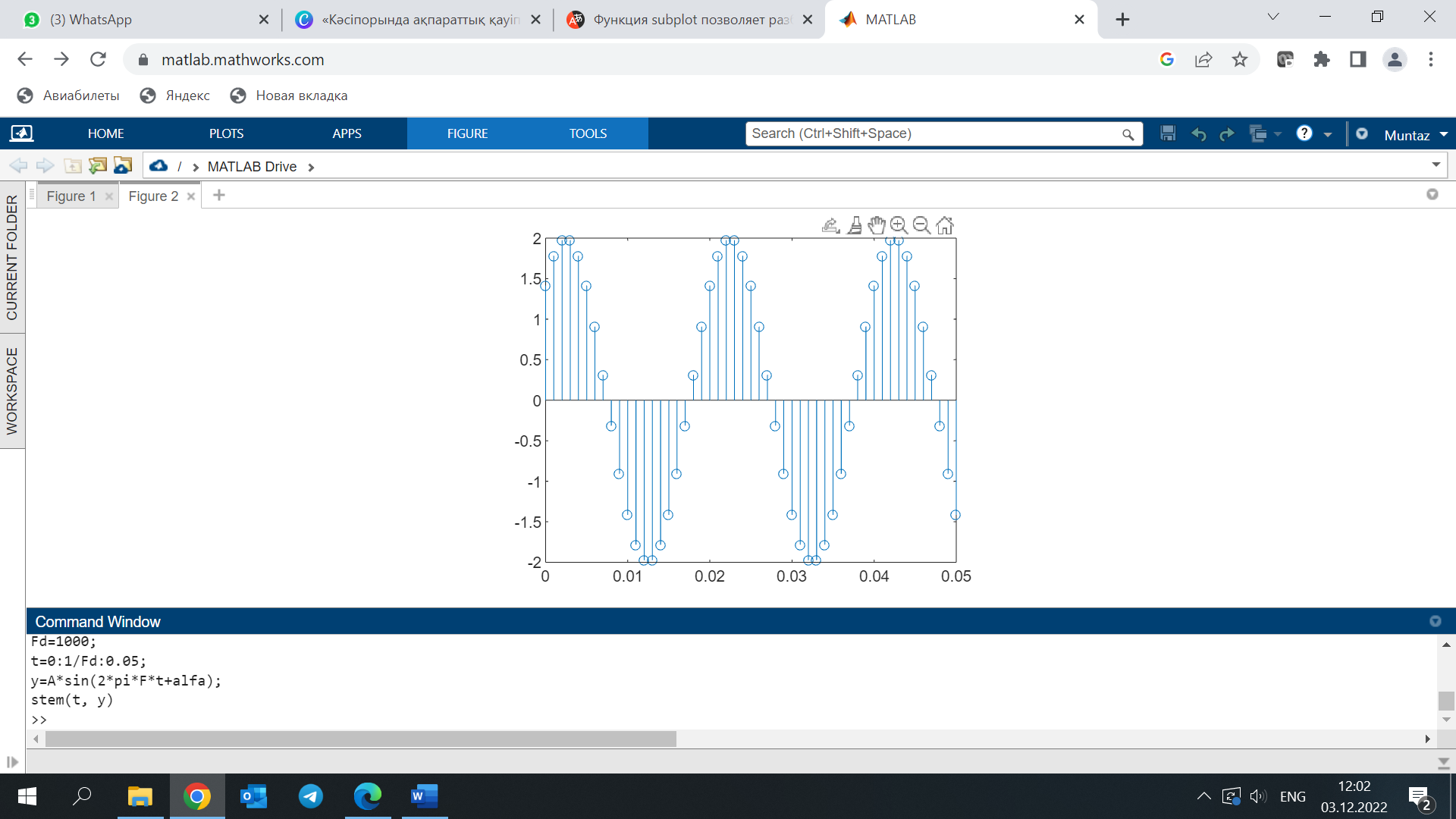
Үш өлшемді графика
t=0:pi/50:10*pi;

x=sin(t);

y=cos(t);

plot3(x,y,t);

grid on


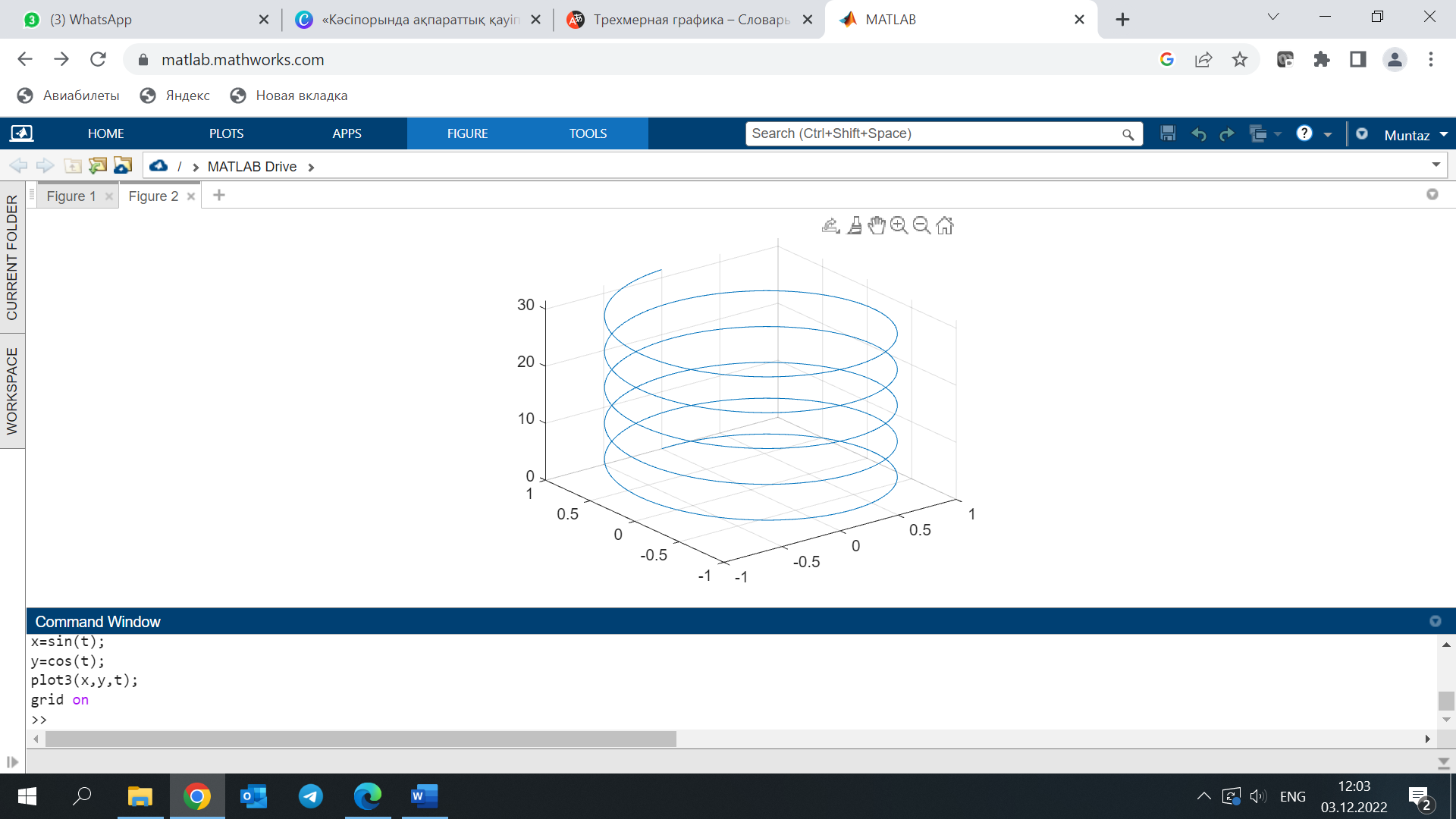
Біз бірінші матрицаны X, ал екіншісін Y деп белгілейміз, ал осы аргументтердегі z=f(x,y) функциясының мәндерінің матрицасын Z әрпімен белгілейміз.

MATLAB жүйесінде арнайы meshgrid функциясы бар бір өлшемді х, у массивтері бойынша X және Y екі өлшемді массивтерді алу. Екі айнымалы функцияның графигін құрудың мысалын қарастырайық z=-x^2 -y^2

x=-2:0.1:2;

y=-1:0.1:1;

[X,Y]=meshgrid(x,y);

Z=-X.^2-Y.^2;

plot3(X,Y,Z);

grid on

Зертханалық жұмыс 3

MATLAB ЖҮЙЕСІНДЕГІ БАҒДАРЛАМАЛАР

Цикл және басқару операторлары:

MATLAB жүйесінің M тілінде операторлардың екі түрі қолданылады цикл. Олардың біріншісінің келесі формасы бар: while өрнек • • • end. Эллипспен көрсетілген код бөлімінің қайталануы жалғасады өрнек «ақиқат» болғанша (нөлге тең емес). Мысалы:



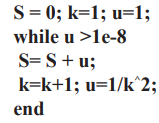
Цикл мәлімдемесінің тағы бір түрі:

varName=өрнек...end үшін, мұндағы varName - айнымалы атауы цикл. Эллипспен белгіленген цикл денесі барлығы үшін орындалады цикл айнымалысының мүмкін мәндері. Мүмкін мәндер жиыны for циклінің айнымалысы кейін келетін өрнекпен анықталады кілт сөз үшін. Мысалы:

---

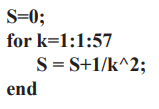
М тіліндегі басқару операторларына шартты оператор мен switch операторы кіреді. Шартты оператор түйінді сөздерді пайдаланады: if, else, elseif (әйтпесе, if), end және үш жолмен қолданылуы мүмкін:




Мысал 1:



Мысалды орындағаннан кейін А массивінің A(2,2) элементі оны өзгертеді

мағынасы. Бұл өзгерісті A және A1 массивтерін салыстыру арқылы қадағалау ыңғайлы.

Шартты сөйлемдерге кіретін шартты өрнектерде сіз жасай аласыз

массивтерді пайдаланыңыз. Егер мұндай массивтің кем дегенде бір элементі нөлге тең болса, онда шарт жалған деп есептеледі. Мысалы:



Бұл мысалда b айнымалысы 2 мәнін қабылдайды, өйткені А матрицасында бір нөлдік элемент бар және барлық шарт жалған болып саналады.

Switch операторы switch (switch), case (case), әйтпесе (басқа жағдайда) кілт сөздерін пайдаланады және келесі пішінге ие:



Мысал 2.



М функциясының денесі функцияны ерте тоқтату және одан шығу үшін қайтару операторымен бірге шартты операторларды жиі пайдаланады. Мысалы:

Зертханалалық жұмыс 4

Жұмыстың мақсаты. Сигналдарды талдауды қалыптастыру үшін MATLAB мүмкіндіктерін зерттеу.

Тапсырма 1. Төменде келтірілген материалды зерттеп, мәтінде келтірілген шаралар мен жаттығуларды қайталаңыз.

Сигналдарды қалыптастыру

Детерминирленген сигналдарды қалыптастыру

Кез-келген өрнекпен берілген іріктелген сигналды қалыптастыру үшін алдымен дискретті уақыт мәндерінің векторын қалыптастыру қажет. Ол үшін FS (sampling frequency) кретизация жиілігінің мәнін орнату және уақыт қатарының қадамы ретінде ну кері мәнін пайдалану ыңғайлы. Үйлесімді тербелістердің қалыптасуының мысалы:

Fs = 8e3;

---

% частота дискретизации

8 кГц t = 0:1/Fs:0.025; % 0.025 с дискретных значений времени

A = 2; % амплитуда – два вольта

f0 = 1e3; % частота

1 кГц phi = pi/4; % начальная фаза

45° s1=A*cos(2*pi*f0*t+phi); % гармоническое колебание

alpha1 = 0.1e3; % скорость затухания

s2 = exp(-alpha1*t) .* s1; % затухающее гармоническое колебание subplot(2,1,1);plot(t,s1); subplot(2,1,2);plot(t,s2);

Суретте. 4.1 төменде келтірілген тербеліс сфераларының "осциллограммалары" көрсетілген



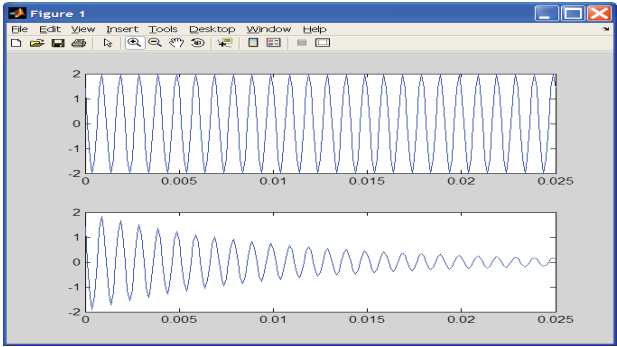
Импульстік сигналдарды қалыптастыру кезінде теңсіздік орындалған кезде бірлікті қайтаратын салыстыру операцияларын және әйтпесе нөлді қолданған жөн, ал векторлық аргумент жағдайында салыстыру нәтижелерінің векторы қайтарылады. Бір жақты экспоненциалды импульсті қалыптастырыңыз (сурет. 4.2):

A = 2; Fs = 8e3;

t = -0.005:1/Fs:0.01;

alpha = 0.5e3;

s = A * exp(-alpha * t) .* (t >= 0);

stem(t,s);



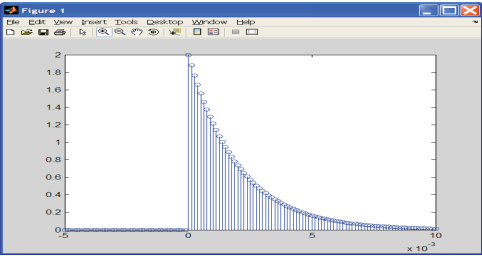
Біз уақытты санаудың басына қатысты орталықтандырылған тікбұрышты импульс қалыптастырамыз (сурет. 4.3):

A = 2;

Fs = 8e3;

T= 0,01;

t = -0,01:1/Fs:0,01;

s = A * (abs(t) <= T/2);

өзек (t, s)


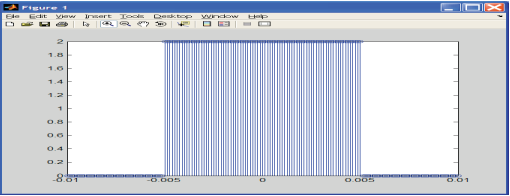
Асимметриялық үшбұрышты импульстің пайда болуының мысалы

(сурет. 4.4):

A = 2;

Fs = 8e3;

T= 0,01;

t = -0,01:1/Fs:0,02;

s = a * t / T .* (t >= 0) .* (t <= T);

stem (t, s)

Зерханалық жұмыс 5

MATLAB ЖҮЙЕСІНДЕГІ ДИСКРЕТТІ СҮЗІРУ

Жұмыс мақсаты. MATLAB-тың сүзу мүмкіндіктерін зерттеу сигналдар.

1-тапсырма. Төмендегі материалды оқып, қайталау, мәтінде берілген шаралар мен жаттығулар.

Краткие теоретические сведения о дискретных фильтрах. В зависимости от наличия обратной связи различают рекурсивные и нерекурсивные фильтры. Наиболее простыми по структуре являются нерекурсивные фильтры. Структура фильтра приведена на рис. 5.1. Нерекурсивные фильтры имеют ограниченную (конечную) во времени импульсную характеристику, поэтому их часто называют КИХ (FIR)-фильтрами. Достоинства нерекурсивных фильтров: они обладают линейной ФЧХ, то есть не вносят фазовых искажений в сигнал

---