Файл: Кафедра математических и естественнонаучных дисциплин Рейтинговая работа.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.04.2024
Просмотров: 14
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Кафедра математических и естественно-научных дисциплин
Рейтинговая работа __Контрольная работа_______________________
по дисциплине Математика_____________________________________
Задание/вариант № 6
Тема* ______________________________________________________________
Выполнена обучающимся группы Розиковой Еленой____________________
(фамилия, имя, отчество)
Преподаватель ____________________________________________________
(фамилия, имя, отчество)
Москва – 2022 г.
Оглавление
Задание 1. Даны матрицы и число . Найти матрицу . 3
Задание 2. Дана система линейных алгебраических уравнений 4
Задание 3. Известны координаты 5
Задание 4. Известны координаты 7
Задание 1. Даны матрицы
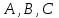 и число
и число 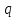 . Найти матрицу
. Найти матрицу 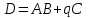 .
.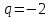 ,
, 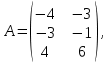
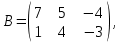
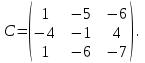
1 действие: А*В =
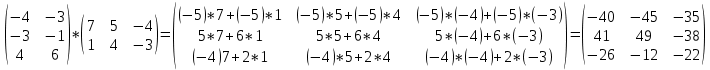
2 действие: q*C =( -2)*
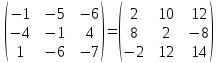
3 действие:D=AB+qC=
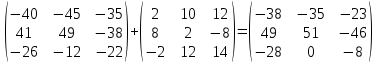
Литература
Линейная алгебра : учеб. пособие / Н.В. Гредасова, М.А. Корешникова, Н.И. Желонкина [и др.] ; Мин-во науки и высш. образования РФ.— Екатеринбург : Изд-во Урал. ун-та, 2019.— 88 с.
Задание 2. Дана система линейных алгебраических уравнений
Найти решение этой системы любым методом.
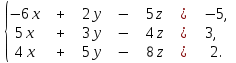
А – основная матрица
В – матрица (столбец) свободных членов
С- расширенная матрица
А =
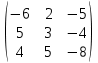 B =
B = 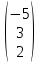
C =
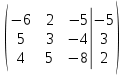
Решаем методом Крамера
1 действие. Вычислим определитель основной матрицы системы:
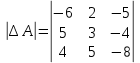 = (-6)*3*(-8) + 2*(-4)*4 + 5*5*(-5) - (-5)*3*4 –
= (-6)*3*(-8) + 2*(-4)*4 + 5*5*(-5) - (-5)*3*4 –(-4)*5*(-6) - 5*2*(-8) = 144-32-125+60-120+80=7
2 действие. Вычислим определитель ∆1. Для этого в матрице А заменим 1 столбец на столбец свободных членов и вычислим определитель получившейся матрицы.
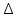 1 =
1 = 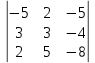 = (-5)*3*(-8)+3*5*(-5)+2*(-4)*2-(-5)*3*2-2*3*(-8)-(-4)*5*(-5)= 120-75-16+30+48-100=7
= (-5)*3*(-8)+3*5*(-5)+2*(-4)*2-(-5)*3*2-2*3*(-8)-(-4)*5*(-5)= 120-75-16+30+48-100=73 действие. Вычислим Δ2. Для этого в матрице A заменим 2-й столбец на столбец свободных членов и вычислим определитель этой матрицы.
∆2 =
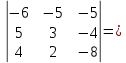 (-6)*3*(-8)+5*2*(-5)+(-5)*(-4)*4 – (-5)*3*4-(-4)*2*(-6)- (-5)*5*(-8) = 144-50+80+60-48-200 = -14
(-6)*3*(-8)+5*2*(-5)+(-5)*(-4)*4 – (-5)*3*4-(-4)*2*(-6)- (-5)*5*(-8) = 144-50+80+60-48-200 = -144 действие. Вычислим Δ3.
Для этого в матрице A заменим 3-й столбец на столбец свободных членов и вычислим определитель этой матрицы.
∆3 =
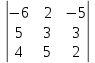 = (-6)*3*2+5*5*(-5)+2*3*4- (-5)*3*4-5*3*(-6)-5*2*2 = -36-125+24+60+90-20 = -7
= (-6)*3*2+5*5*(-5)+2*3*4- (-5)*3*4-5*3*(-6)-5*2*2 = -36-125+24+60+90-20 = -7Вычисляем значения переменных:
X1 =
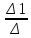 =
= 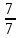 = 1
= 1X2 =
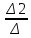 =
= 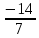 = -2
= -2 X3 =
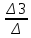 =
= 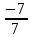 = -1
= -1Ответ: x1 = 1; x2 =- 2; x3 = -1
Задание 3. Известны координаты
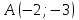 | 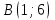 | 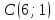 |
в прямоугольной системе координат
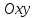 трех точек
трех точек 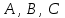 , являющихся вершинами треугольника. Изобразить треугольник
, являющихся вершинами треугольника. Изобразить треугольник 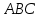
в этой прямоугольной системе координат и найти:
3.1 координаты векторов
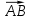 ,
, 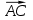 и их длины;
и их длины;AB = {хB-хA;уB-уA}={1-(-2); 6-(-3)} = {3;9}
АС = { хС-хA;уС-уA} = {6-(-2);1-(-3)} = {8;4}
|АВ| =
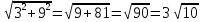
|АС| =
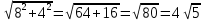
3.2 скалярное произведение векторов
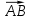 ,
, 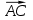 и угол
и угол 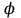 между векторами
между векторами 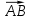 ,
, 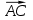 ;
;АВ*АС = 3*8+9*4 = 24+36 = 60
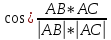 =
= 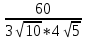 =
= 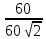 =
= 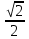
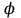 =
= 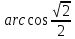 = 45º
= 45º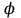 = 45º
= 45º3.3 векторное произведение векторов
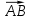 ,
, 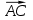 и площадь треугольника
и площадь треугольника 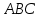 ;
;Найдем вектора по координатам точек
AB = {Bx - Ax; By - Ay; Bz - Az} = {1 - (-2); 6 - (-3); 0 - 0} = {3; 9; 0}
AC = {Cx - Ax; Cy - Ay; Cz - Az} = {6 - (-2); 1 - (-3); 0 - 0} = {8; 4; 0}
S=
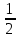 |AB × AC|
|AB × AC|Найдем векторное произведение векторов
c = AB × AC
АB × AC =
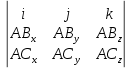 =
=  = i* (9·0 - 0·4) - j *(3·0 - 0·8) + k* (3·4 - 9·8) = i *(0 - 0) - j *(0 - 0) + k* (12 - 72) = {0; 0; -60}
= i* (9·0 - 0·4) - j *(3·0 - 0·8) + k* (3·4 - 9·8) = i *(0 - 0) - j *(0 - 0) + k* (12 - 72) = {0; 0; -60}Найдем длину (модуль) вектора
|c| =
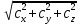
=
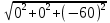 =
= 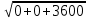 =
= 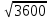 = 60
= 60Найдем площадь треугольника:
S =
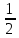 · 60 = 30
· 60 = 303.4 значение параметра
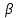 , при котором векторы
, при котором векторы 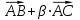 и
и 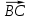 будут коллинеарны;
будут коллинеарны;3.5 координаты точки
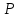 , делящей отрезок
, делящей отрезок 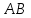 в отношении
в отношении 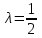 ;
;3.6 каноническое уравнение стороны
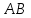 ;
;Воспользуемся формулой канонического уравнения
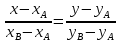
Подставим в формулу координаты
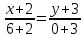
Упростим выражение, выразив y через X
y =
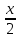 - 2
- 23.7 уравнение с угловым коэффициентом и угловой коэффициент прямой, проходящей через точку
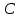 параллельно прямой
параллельно прямой 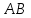 ;
;Литература
Ермилова, Н.А., Павельчук, А.В. Е73 Матрицы, определители, системы линейных уравнений: Учебно-методи- ческое пособие / Н.А. Ермилова, А.В. Павельчук. – Благовещенск: Амурский гос. ун-т, 2013. – 68 с.
Задание 4. Известны координаты
| 6 | 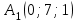 | 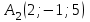 | 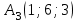 | 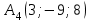 |
в прямоугольной системе координат
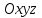 вершин пирамиды
вершин пирамиды 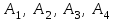 .
.4.1. Найти смешанное произведение векторов
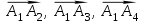 и объем пирамиды
и объем пирамиды 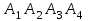 ;
;Найдем вектора по координатам точек:
A1А2 = {А2x - A1x; А2y - A1y; А2z - A1z} = {2 - 0; -1 - 7; 5 - 1} = {2; -8; 4}
A1А3 = {А3x - A1x; А3y - A1y; А3z - A1z} = {1 - 0; 6 - (-7); 3 - 1} = {1; 13; 2}
A1А4 = {А4x - A1x; А4y - A1y; А4z - A1z} = {3 - 0; -9 - 7; 8 - 1} = {3; -16; 7}
Найдем смешанное произведение векторов:
A1А2 · (A1А3 × A1А4) =
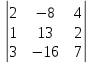 =2·13·7 + (-8)·2·3 + 4·1·(-16) - 4·13·3 - (-8)·1·7 - 2·2·(-16) =
=2·13·7 + (-8)·2·3 + 4·1·(-16) - 4·13·3 - (-8)·1·7 - 2·2·(-16) == 182 - 48 - 64 - 156 + 56 + 64 = 34
Найдем объем пирамиды:
V =
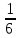 · 34 =
· 34 = 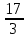
4.2. Найти каноническое уравнение прямой
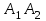 ;
;Воспользуемся формулой канонического уравнения прямой
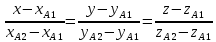
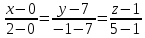
В итоге получено каноническое уравнение прямой:
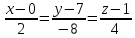
4.3. Найти общее уравнение плоскости
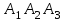 ;
;Для составления уравнения плоскости используем формулу:
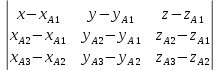 =0
=0 Подставим данные и упростим выражение:
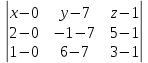 = 0
= 0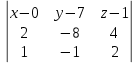 =0
=0(x – 0)*(-8·2-4·(-1) )- (y – 7)*(2·2-4·1 )+ (z – 1)*(2·(-1)-(-8)·1) = 0
(-12)*x - 0 + 0*y - 7 + 6*z - 1 = 0
- 12x + 6z - 6 = 0
2x - z + 1 = 0
Литература
Линейная алгебра и аналитическая геометрия : учеб.-метод. пособие / авт.-сост.: В. А. Феофанова, Ю. Г. Мартышенко; М-во образования и науки РФ ; ФГАОУ ВПО «УрФУ им. первого Президента России Б.Н.Ельцина», Нижнетагил. технол. ин-т. (фил.). – Нижний Тагил : НТИ (филиал) УрФУ, 2013. – 148 с.

