Файл: Удк Численные методы решения дифференциальных уравнений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 19
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
УДК:
Численные методы решения дифференциальных уравнений
Ковалев С.А.
Студент 2-го курса Ухтинский государственный технический университет, г. Ухта, Россия,
Научный руководитель: Мотрюк Е.Н.
Зав. Кафедрой высшей математики, к. т. н., доцент ФГБОУ ВО Ухтинский государственный технический университет, г. Ухта, Россия,
Цель работы: Изучить, как с помощью численного метода решать дифференциальные уравнения с применением различных методов вычислений в программном средстве вычислений MathCAD.
Задачи:
-
Изучить теоретический материал по теме: «дифференциальные уравнения»; -
Разобрать материал по теме: «численный метод дифференциальных уравнений»; -
Изучить различные методы вычисления дифференциальных уравнений; -
На основе теоретического материала составить конспект; -
Провести практику вычислений в программном средстве вычислений Mathad; -
Сформулировать выводы по проделанной работе.
«Числа правят миром» - слова известного философа Платона. Эти слова актуальны и по сей день, ведь весь наш мир состоит из математического моделирования и численных методов в самых различных областях жизни человека. Ведь считать человеку приходилось еще с древних времен. Начиная с египетских папирусов заканчивая многочисленными математическими таблицами. Так с появлением компьютерных технологий в жизни человека автоматизированные вычисления больших масштабов стали важным инструментом в науке и технике. От сюда началась новая область математики «Численный метод».
В эту область входит и способ решения дифференциальных уравнений. Дифференциальные уравнения являются одним из основных методов решения задач. Ведь без вычисления дифференциальных уравнений не обойдется ни один инженер-исследователь. На дифференциальных уравнения строятся многие задачи механики, химии, физики и других отраслей науки.
В зависимости от числа независимых переменных дифференциальные уравнения делятся на две существенно различные категории: обыкновенные дифференциальные уравнения, содержащие одну независимую переменную, и уравнения с частными производными, содержащие несколько независимых перемен.
Обыкновенными дифференциальными уравнениями называются такие уравнения, которые содержат одну или несколько производных от искомой функции
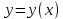 . Их мы и будем рассматривать с помощью вычисления численным методом.
. Их мы и будем рассматривать с помощью вычисления численным методом.Существует несколько видов методов вычисления численного дифференцирования.
-
Геометрическая интерпретация решения; -
Метод Эйлера; -
Метод Рунге-Кутта (четвертого порядка); -
Метод матричной экспоненты.
Для рассмотрения каждого из видов метода вычисления численного дифференцирования рассмотрим задачу Коши. Найти решение обыкновенного дифференциального уравнения
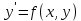 , где
, где 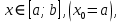 удовлетворяющие начальному условию
удовлетворяющие начальному условию 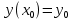 . При численном решении поставленной задачи отрезок
. При численном решении поставленной задачи отрезок  разбивают на
разбивают на 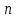 частей (не обязательно равных) и определяют приближенные значения искомой функции
частей (не обязательно равных) и определяют приближенные значения искомой функции 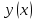 в точках деления
в точках деления 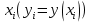 .[1, стр 59]
.[1, стр 59] -
Геометрическая интерпретация решения
Геометрический смысл решения обыкновенного дифференциального уравнения первого порядка методом Эйлера (методом Рунге-Кутта первого порядка) состоит в том, что на малом
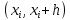 отрезке интегральная кривая
отрезке интегральная кривая 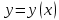 дифференциального уравнения заменяется отрезком ее касательной в точке
дифференциального уравнения заменяется отрезком ее касательной в точке 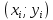 .
.-
Метод Эйлера
Приближённое значение в точке
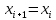 находится по формуле:
находится по формуле: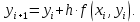
-
Метод Рунге-Кутта (четвертого порядка)
Этот метод получил наиболее широкое распространение в практических расчетах. Его погрешность оценивается величиной
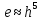 , что дает возможность получить более точные результаты, чем в методе Эйлера. Не давая полного описания вывода формул, приведем их в следующем виде:
, что дает возможность получить более точные результаты, чем в методе Эйлера. Не давая полного описания вывода формул, приведем их в следующем виде: 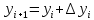
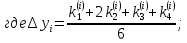
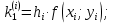
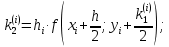
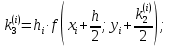
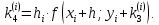
Здесь символом
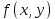 так же, как и в выше описанном методе Эйлера, обозначается правая часть решаемого дифференциального уравнения,
так же, как и в выше описанном методе Эйлера, обозначается правая часть решаемого дифференциального уравнения, 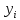 и
и 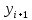 - приближённые значения интегральной функции соответственно в точках
- приближённые значения интегральной функции соответственно в точках 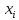 и
и 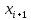 ,
, 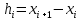 .
.-
Метод матричной экспоненты
Экспонента матрицы — матричная функция от квадратной матрицы, аналогичная обычной экспоненциальной функции. Матричная экспонента устанавливает связь между алгеброй Ли матриц и соответствующий группой Ли.
Для вещественной или комплексной матрицы размера , обозначаемая как или , — это матрица, определяемая степенным рядом:
,где — k-я степень матрицы . Данный ряд всегда сходится, так что экспонента от всегда корректно определена.
Если — матрица размера , то матричная экспонента от есть матрица размерности , единственный элемент которой равен обычной экспоненте от единственного элемента.
Рассмотрим пример решения задачи Коши в mathcad. Будем решать двумя способами: Рунге-Кутта и методом матричной экспоненты.
1 Метод Рунге-Кутта
Для решения систем дифференциальных уравнений используются функция rkfixed.
Функция rkfixed(y, x1, x2, npoints, D) возвращает матрицу. Первый столбец этой матрицы содержит точки, в которых получено решение, а остальные столбцы – решения и его первые производные.
Аргументы функции:
y–вектор начальных значений (n элементов).
x1 и x2 – границы интервала, на котором ищется решение дифференциального уравнения.
npoints – число точек внутри интервала (x1,x2), в которых ищется решение. Функция rkfixed возвращает матрицу, состоящую из 1+npoints строк.
D – вектор, состоящий из n элементов, который содержит первые производные искомой функции.
2 Метод матричной экспоненты
Если матричная экспонента известна, то решение задачи Коши вычисляется по универсальной формуле
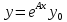 с различными начальными условиями
с различными начальными условиями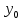 .
.Матрицу системы можно привести к диагональной форме, если она имеет собственный базис – базис из собственных векторов, и тогда решение задачи Коши может быть записано в виде:
 , где С – матрица перехода от исходного базиса к собственному базису матрицы А, Λ – матричная экспонента, записанная в собственном базисе матрицы А. Матрицы жестких систем таковы, что погрешности вычисления С и С-1 приводят к совершенно недостоверным результатам.[2,стр 334]
, где С – матрица перехода от исходного базиса к собственному базису матрицы А, Λ – матричная экспонента, записанная в собственном базисе матрицы А. Матрицы жестких систем таковы, что погрешности вычисления С и С-1 приводят к совершенно недостоверным результатам.[2,стр 334] Рассмотрим фрагмент рабочего документа Mathcad, содержащий решение задачи Коши для жесткой системы по формуле
 .
. Для точного выполнения работы воспользуемся и аналитическим способом решения задачи Коши.
Найти приближённое решение задачи Коши
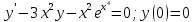
методом Эйлера на заданном отрезке
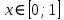 с шагом h = 0,1 .
с шагом h = 0,1 .Решение:
Для начала, найдем точное решение этого линейного уравнения первого порядка

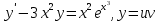
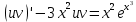
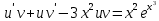
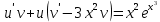
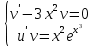
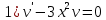
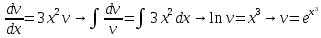
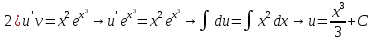
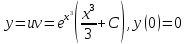
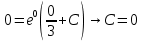
Тогда точное решение имеет вид :
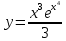
Теперь найдем численное приближенное решение методом Эйлера, с шагом
h=0,1.
Общий вид: Уравнение
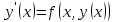 , формула:
, формула: 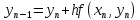
В этом случае:
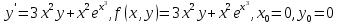
Тогда формулы имеет вид:
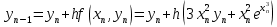
Используя эту формулу решаем задачу. Полученные данные запишем в таблицу.
| n | 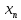 | 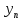 | Точное значение |
| 0 | 0 | 0 | 0 |
| 1 | 0,1 | 0 | 0,000334 |
| 2 | 0,2 | 0,001001 | 0,002688 |
| 3 | 0,3 | 0,005045 | 0,009246 |
| 4 | 0,4 | 0,014428 | 0,022743 |
| 5 | 0,5 | 0,032178 | 0,047215 |
| 6 | 0,6 | 0,062920 | 0,089359 |
| 7 | 0,7 | 0,114395 | 0,161115 |
| 8 | 0,8 | 0,200260 | 0,284779 |
| 9 | 0,9 | 0,345502 | 0,503741 |
| 10 | 1 | 0,597372 | 0,906094 |

