Файл: Отчет по научноисследовательской работе разработка и исследование методов машинного обучения для составления оптимального портфеля ценных бумаг.docx
Добавлен: 16.10.2024
Просмотров: 30
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Теорема сходимости перцептрона, доказанная Ф. Розенблаттом говорит о том, что элементарный перцептрон, обучаемый по вышеописанному алгоритму, независимо от начального состояния весовых коэффициентов и последовательности появления стимулов всегда приведёт к достижению решения за конечный промежуток времени [7].
2.3 Метод обратного распространения ошибки
Для обучения многослойных сетей некоторыми учеными, в том числе Д. Румельхартом, был предложен градиентный алгоритм обучения с учителем, проводящий сигнал ошибки, вычисленный выходами перцептрона, к его входам, слой за слоем. Сейчас это самый популярный метод обучения многослойных перцептронов. Его преимущество в том, что он может обучить все слои нейронной сети, и его легко просчитать локально. Однако этот метод является очень долгим, к тому же, для его применения нужно, чтобы передаточная функция нейронов была дифференцируемой. При этом в перцептронах пришлось отказаться от бинарного сигнала, и пользоваться на входе непрерывными значениями [7].
На каждой итерации алгоритма обратного распространения весовые коэффициенты нейронной сети модифицируются так, чтобы улучшить решение одного примера. Таким образом, в процессе обучения циклически решаются однокритериальные задачи оптимизации.
Обучение нейронной сети характеризуется четырьмя ограничениями, выделяющими обучение нейросетей из общих задач оптимизации: огромное число параметров, необходимость высокого уровня параллелизма при обучении, многокритериальность решаемых задач, достаточно широкая область, в которой значения всех минимизируемых функций близки к минимальным. В остальном проблему обучения можно, как правило, сформулировать как задачу минимизации оценки. Минимизация оценки – сложная проблема: параметров очень много (для стандартных примеров от сотни до миллиона), график оценки функции от подстраиваемых параметров может содержать много локальных минимумов [8].
Несмотря на многочисленные успешные применения обратного распространения, данный метод не является универсальным решением. Огромный недостаток – неопределённо долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться целые дни или недели, кроме того, она может и не обучиться вовсе.
Градиентный спуск может найти локальный минимум вместо глобального (рисунок 3).
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших выходных значениях, а производная активирующей функции будет очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть.
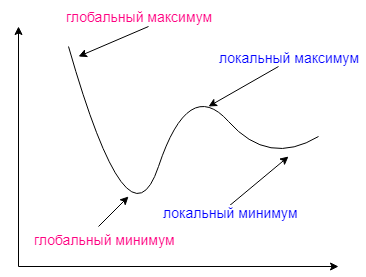
Рисунок 3 – Недостаток градиентного спуска
Градиентный спуск с обратным распространением ошибок гарантирует нахождение только локального минимума функции; также, возникают проблемы с пересечением плато на поверхности функции ошибки.
2.4 Генетический алгоритм
Генетиический алгориитм – эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, аналогичных естественному отбору в природе.
Случайным образом создаётся множество генотипов начальной популяции. Они оцениваются с использованием «функции приспособленности», в результате чего с каждым генотипом ассоциируется определённое значение (приспособленность), которое определяет, насколько хорошо фенотип, им описываемый, решает поставленную задачу.
Из полученного множества решений (поколения) с учётом значения приспособленности выбираются решения (лучшие особи имеют большую вероятность быть выбранными), к которым применяются генетические операторы, например, «скрещивание» и «мутация», результатом чего является получение новых решений. Для них аналогично вычисляется значение приспособленности, затем производится отбор лучших решений в следующее поколение [9].
Вышеперечисленные действия повторяется итеративно, таким образом моделируется «эволюционный процесс», который продолжается несколько жизненных циклов (поколений), пока не будет выполнен критерий остановки алгоритма. Таким критерием может быть:
-
нахождение глобального, либо субоптимального решения; -
исчерпание числа поколений, отпущенных на эволюцию; -
исчерпание времени, отпущенного на эволюцию.
Преимущества генетического алгоритма:
-
большое число свободных параметров, позволяющим эффективно встраивать эвристики; -
эффективное распараллеливание; -
работает заведомо не хуже абсолютно случайного поиска; -
связь с биологией, дающая некоторую надежду на исключительную эффективность ГА в природе.
Недостатки:
-
недоказанность сходимости; -
в простых целевых функциях (гладкие, один экстремум и т.п.) генетика всегда проигрывает по скорости простым алгоритмам поиска.
Во многих задачах генетические алгоритмы имеют тенденцию сходиться к локальному оптимуму или даже к произвольной точке, но не к глобальному оптимуму для данной задачи. Такие алгоритмы не хотят жертвовать кратковременной высокой пригодностью для достижения долгосрочной пригодности.
Заключение
За время выполнения НИР была подобрана и изучена научная литература по выбранной теме исследований, обоснована актуальность выбранной темы научно-исследовательской работы на основе анализа литературных источников.
Также проведен обзор методов машинного обучения для составления оптимального портфеля ценных бумаг.
Рассмотрены следующие методы машинного обучения:
- нейронные сети;
- метод коррекции ошибки;
- метод обратного распространения ошибки;
- генетический алгоритм.
Отчет по научно-исследовательской работе оформлен в соответствии с требованиями, предъявляемыми к выпускной квалификационной работе магистра.
Список использованной литературы
-
Доля частных инвесторов на рынке акций Московской биржи [Электронный ресурс]. URL: https://www.moex.com/n53380/?nt=106 (дата обращения: 07.11.2022). -
Сколько новых инвесторов пришло на биржу в 2021 [Электронный ресурс]. URL: https://bcs-express.ru/novosti-i-analitika/skol-ko-novykh-investorov-prishlo-na-birzhu-v-2021 (дата обращения: 10.11.2022). -
Распоряжение Президента Российской Федерации от 9 мая 2017 г. № 203 «Стратегия развития информационного общества в Российской Федерации на 2017 – 2030 годы». [Электронный ресурс]. URL: http://zmedu.hostedu.ru/files/ykaz_7668.pdf (дата обращения: 12.11.2022). -
Программа «Цифровая экономика Российской Федерации». Утверждена распоряжением Правительства Российской Федерации от 28 июля 2017 г. № 1632-р. [Электронный ресурс]. URL: http://static. government.ru/media/files/9gFM4FHj4PsB79I5v7yLVuPgu4bvR7M0.pdf (дата обращения: 14.11.2021). -
Галкина С. А. Использование методов машинного обучения для построения оптимального портфеля ценных бумаг / Галкина С. А. International Journal of Open Information Technologies -
Персептрон Розенблатта – машина, которая смогла обучаться [Электронный ресурс]. URL: https://neurohive.io/ru/osnovy-data-science/perseptron-rozenblatta-mashina-kotoraja-smogla-obuchatsja/ (дата обращения: 04.12.2022). -
Обучение с учителем. Метод коррекции ошибки. Метод обратного распространения ошибки [Электронный ресурс]. URL: https://intellect.icu/obuchenie-s-uchitelem-metod-korrektsii-oshibki-metod-obratnogo-rasprostraneniya-oshibki-117 (дата обращения: 11.12.2022). -
Нейчев Р., Федотов С. Метод обратного распространения ошибки [Электронный ресурс]. URL: https://academy.yandex.ru/handbook/ml/article/metod-obratnogo-rasprostraneniya-oshibki (дата обращения: 10.12.2022). -
Искусственный интеллект. Генетический алгоритм и его применения [Электронный ресурс]. URL: https://3dnews.ru/1050009/iskusstvenniy-intellekt-geneticheskiy-algoritm-i-ego-primeneniya (дата обращения: 15.12.2022).
