Файл: Курсовая работа по курсу математическая экономика.docx

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
САМАРСКИЙ УНИВЕРСИТЕТ

SAMARAUNIVERSITY
федеральное государственное автономное образовательное учреждение высшего образования «Самарский национальный исследовательский университет имени академика С.П. Королева»
Институт экономики и управления

Кафедра математических методов в экономике
КУРСОВАЯ РАБОТА
ПО КУРСУ «МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА»

тема: «Экономико - математическое моделирование фирмы (на примере Торгового дома сельско-хозяйственного производства «Домик в деревне»)»

Вариант №6

Выполнила: Доценко А.С.,

студентка группы: 7250-380305D

Проверил:

Профессор Гераськин М.И.

Рецензент:


Самара 2023

ВВЕДЕНИЕ

Экономико-математическое моделирование коммерческой деятельности производственной фирмы на различных типах потребительских рынков происходит по-разному, поэтому необходимо учитывать особенности каждого из них при оптимизации производственной деятельности. В данной курсовой работе выполнены следующие задачи:

• 
  формирование экономико-математических моделей производственных процессов фирм в виде производственных функций;
  
• 
  разработка моделей издержек производственных фирм в виде функций издержек;
  
• 
  анализ тенденций развития потребительских рынков и определений функций потребительского спроса;
  
• 
  разработка оптимизационных моделей коммерческой деятельности производственных фирм и определение оптимальной производственной программы на различных типах потребительских рынков;
  
• 
  проверка условий равновесия производства и потребления.
  

Благодаря данному исследованию будут изучены различные типы производственных функций и типы рынков.

Самарская область – один из ключевых регионов нашей страны. На её территории функционирует около 860 крупных и средних промышленных предприятий. В нашей области реализуется кластерная политика, которая представляет собой систему государственных и общественных мер и механизмов поддержки кластеров и кластерных инициатив, обеспечивающих повышение конкурентоспособности регионов, предприятий, входящих в кластер,

---

развитие институтов, стимулирующих формирование кластеров, а также обеспечивающих внедрение инноваций.

Агропромышленный комплекс, представляющий собой многоотраслевую производственно-экономическую систему, в которой функционируют около 460 крупных сельскохозяйственных предприятий, 2,2 тысячи крестьянских (фермерских) хозяйств, 267,2 тыс. личных подсобных хозяйств и около 780 пищевых, перерабатывающих организаций и предприятий, также является ключевым направлением в развитии региона.

Благодаря оптимизационной деятельности в данной системе, можно добиться улучшения не только нескольких показателей, но и отрасли в целом. Развитие конкурентно способности предприятий региона поможет привлекать инвесторов для создания новых и улучшения существующих проектов, что благоприятно скажется на экономике области в целом.

1.1. Анализ бизнес-процесса корпорации.

Сельскохозяйственная компания занимается производством молока и поставляет часть товара своему партнёру по производству кисломолочных продуктов, а остальное сбывает на монополистический рынок.



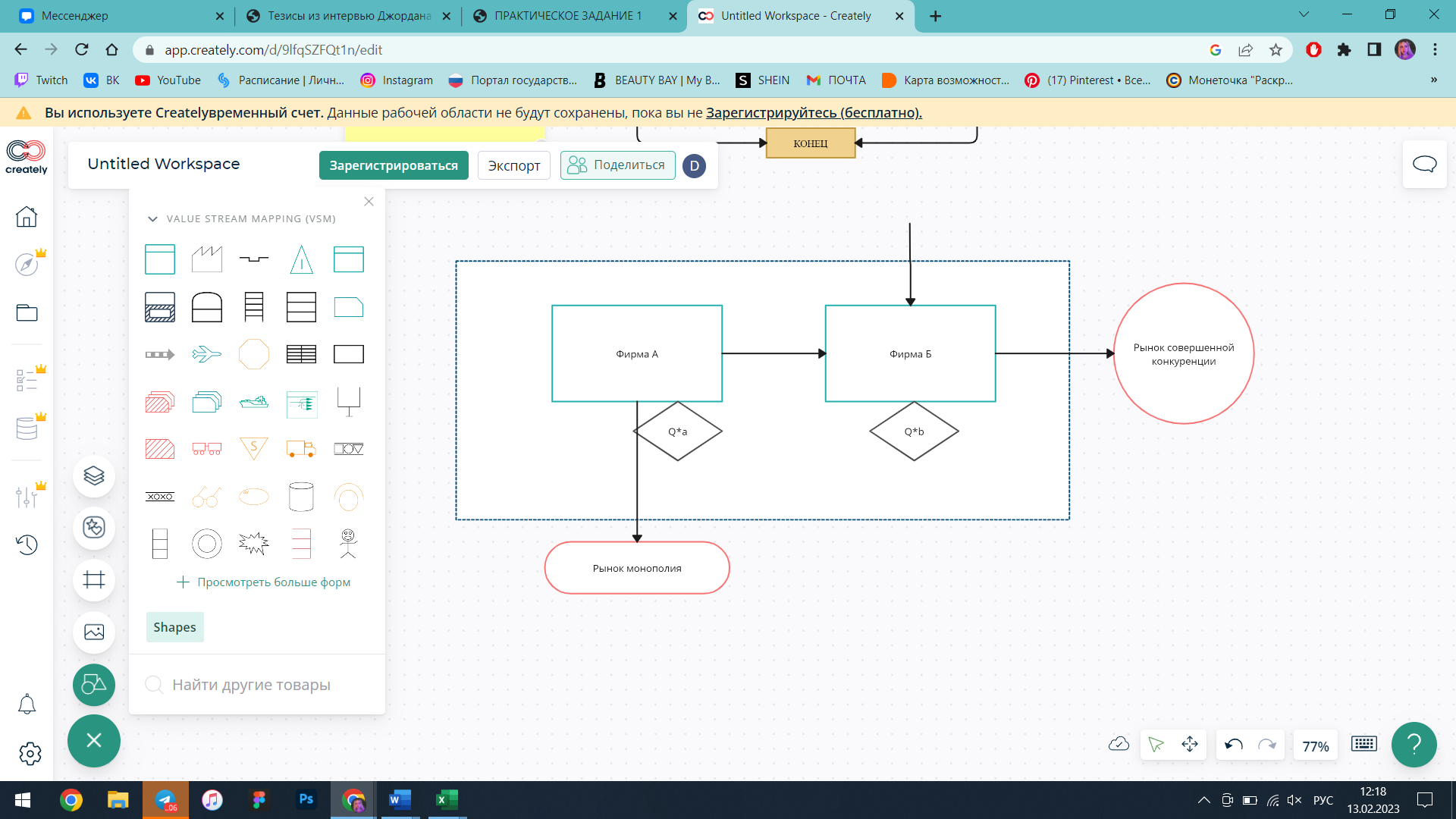
Рисунок 1 – Схема агентов рынка

1.2. АНАЛИЗ КРИВЫХ ВЫПУСКА ХОЛДИНГА

Используя данные о затратах ресурсов: труда и капитала, а также о количестве выращенной продукции: молока за 5 лет, проанализируем деятельность фирмы. А точнее построим кривую выпуска ООО «Молоко», отражающую зависимость объёма молока от затраченного капитала (рисунок 2). Для того, чтобы наглядно убедиться в том, что для данной технологии используется производственная функция Кобба – Дугласа (ресурсы взаимодополняемые), построим линию тренда. Наилучшую аппроксимацию показала степенная, следовательно, предположение о виде производственной функции было сделано верно.



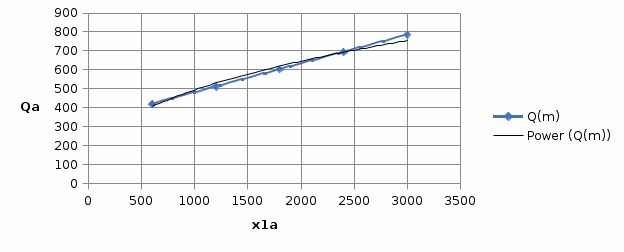
Рисунок 1 - Кривая выпуска ООО "Молоко"

---

Фирма А
x1(K, ед.)	х2(L, чел.)	Q(m)
600	372	419,4
1200	384	510,6
1800	396	601,8
2400	408	693
3000	420	784,2
3600	504	810,0

Фирма В
x1(АИ, m)	x2(АИМ, m)	Q(m)
331,2	43	1694,4
398,4	46	1900,2
465,6	49	2106
532,8	52	2311,8
600	55	2517,6
660	60,5	1565,2

Теперь перейдём к анализу деятельности ООО «Домик в деревне», у которой также известны данные о полученных ресурсах: «Домик в деревне», молоко от поставщика извне, а также о количестве произведённой продукции: молока «Домик в деревне» за 5 лет. А точнее построим кривую выпуска ООО «Молоко», отражающую зависимость объёма выпущенного продукта от поставленного молока (рисунок 3). Для того, чтобы наглядно убедиться в том, что для данной технологии используется линейная производственная функция (ресурсы взаимозаменяемые), построим линию тренда. Наилучшую аппроксимацию показала линейная, следовательно, предположение о виде производственной функции было сделано верно.

---

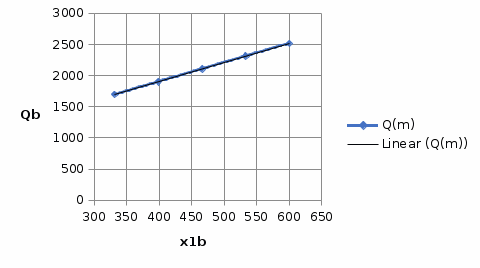
Рисунок 2 - Кривая выпуска ООО "Молоко"

В силу того, что графики подтвердили наши предположения о видах производственных функции организаций, необходимо найти их коэффициенты.

Для этого воспользуемся методом наименьших квадратов (МНК) и встроенной надстройкой «Поиск решения» в Microsoft Excel. Порядок выполненных действий представлен ниже:

1. 
   Начнём с метода наименьших квадратов, так как он позволяет определить целевую функцию, которая необходима для «Поиска решений». Функция Кобба – Дугласа имеет вид: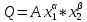 (1). Так как МНК предполагает квадрат разности исходной Q и Q(х) оптимальной, то предположим, что все коэффициенты равны 1, и найдём Q(х).
   
2. 
   Теперь найдём квадрат разности (Q -Q(х))² (2), а затем подсчитаем сумму полученных значений, ячейку с которой и будем применять в качестве целевой функции.
   
3. 
   На вкладке «Данные» выберем «Поиск решения». Укажем целевую функцию (как раз сумма квадратов разностей), а также изменяемые ячейки (неизвестные коэффициенты). Кроме того, необходимо указать, что мы минимизируем целевую ячейку, так как желательно, чтобы отклонения фактических значений от оптимальных было меньше.
   

---