Файл: Методические указания по выполнению контрольной работы Введение Изучение дисциплины Теория кодирования.doc

М ИНОБРНАУКИ РОССИИ

АЛАТЫРСКИЙ ФИЛИАЛ

Федерального государственного бюджетного образовательного учреждения

высшего профессионального образования

«Чувашский государственный университет имени И.Н.Ульянова»

Факультет управления и экономики

Кафедра Высшей математики и информационных технологий


ТЕОРИЯКОДИРОВАНИЯ

группа ЗАФТ – 03 – 12

2 курс (3 семестр)

Преподаватель: асс. Турайкина Е.В.

Алатырь 2013

ТЕОРИЯ КОДИРОВАНИЯ
Методические указания по выполнению контрольной работы
Введение

Изучение дисциплины «Теория кодирования» предусмотрено Государственным образовательным стандартом высшего профессионального образования, регламентирующими процесс подготовки бакалавров по специальности 010500 «Математическое обеспечение и администрирование информационных систем». В соответствии с этими же стандартами данная дисциплина должна быть обеспечена практикумом.

Контрольная работа по дисциплине «Теория кодирования» нацелена на ознакомление студентов с основными методами кодирования информации.
Общие методические указания

Задания носят теоретический и практический характер и заключаются в решении задач и ответах на вопросы. Задания выполняются в строгой последовательности: сначала указывается условие, затем ответ. Контрольная работа выполняется в письменном виде в виде распечаток результата выполненного задания. Объем контрольной работы не должен превышать 20 печатных страниц. Работа должна быть грамотно написана, правильно оформлена. Страницы нумеруются, ставится номер варианта. В конце работы указывается список используемой литературы. Номер варианта соответствует порядковому номеру студента в списке группы.

Контрольную работу необходимо представить в сроки, указанные в учебном графике. Работы, не отвечающие требованиям методических указаний, не засчитываются.

Перечень дисциплин, усвоение которых необходимо студентам для изучения данной дисциплины:

• 
  информатика;
  
• 
  математическая логика;
  
• 
  дискретная математика;
  
• 
  программирование.
  

Контрольная работа оформляется в следующем виде:

1. 
   титульный лист;
   
2. 
   содержание;
   
3. 
   затем приводятся:
   

для теоретических заданий – вариант ответа;

для практических заданий – распечатки результатов выполненной работы на компьютере и описание проделанных действий.

---

4. 
   список использованной литературы.
   

Задание №1. Теоретическая часть

При выполнении данного задания необходимо более полно раскрыть поставленную тему приведением всех необходимых ссылок на использованные источники литературы.

№ варианта	Индивидуальная тема
1	Подстановочные и перестановочные шифры. Шифры Цезаря, Виженера, Вернома.
2	Электронная цифровая подпись: основные понятия и определения. Электронная подпись на основе алгоритма RSA.
3	Алгоритм цифровой подписи Эль-Гамаля (EGSA). Алгоритм цифровой подписи DSA.
4	Понятие помехоустойчивого кодирования.
5	Основные характеристики кодов.
6	Циклические коды: порождающий полином, порождающая матрица. Код Рида-Соломона.
7	Компьютерные преступления и особенности их расследования.
8	Нормативно-правовая база защиты компьютерных сетей от несанкционированного доступа.
9	Цифровой дайджест и хэш-функция
10	Принцип построения кодов Хэмминга для коррекции одиночных и обнаружения двоичных ошибок.
11	Шенноновская модель дискретного канала и его пропускная способность.
12	Циклические коды. Код Рида-Соломона.
13	Циклические коды. Код БЧХ.
14	Коды с обнаружением ошибок (коды с четным количеством единиц, коды с удвоением единиц, инверсный код).
15	Пропускная способность передачи информации и ее согласования с потоком информации от источника.

Задание №2. Практическая часть

Задание 2.1. Моделирование процесса кодирования в АЛУ компьютера

Необходимо разработать структурную схему комбинационного устройства, вычисляющего заданную логическую функцию. Моделировать работу устройства, используя среду EXCEL.

---

По заданной таблице истинности составить аналитическое выражение для функции Y(X1,X2,Х3). Оформить таблицу, в которую занести произвольные данные для Х1,Х2,X3. Столбец функции Y вычислять при помощи формулы. Дополнить таблицу столбцом Т, занести в него отсчеты моментов времени, в которые поступали на устройство сигналы Х1, Х2, X3. По таблице построить диаграмму работы устройства в виде отдельных гистограмм вида X1(T), X2(T), …Y(T), где Т – равноотстоящие отсчеты времени. Заполняя таблицу произвольными данными, следить за изменениями на диаграмме.
Варианты заданий:

X1	X2	X3	Y(X1,X2,X3) по вариантам
			1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0	1	1
0	0	1	1	0	1	1	1	0	0	1	0	1	1	0	1	0	0
0	1	0	1	0	1	1	1	0	0	1	0	0	1	0	1	0	0
0	1	1	1	1	0	0	0	1	0	0	1	0	0	0	1	1	1
1	0	0	1	0	1	0	1	0	0	1	1	1	0	0	1	0	0
1	0	1	1	1	0	0	0	1	0	0	0	0	0	1	1	1	1
1	1	0	1	1	0	0	0	1	0	0	0	0	0	1	1	1	1
1	1	1	0	0	0	0	0	1	1	0	0	0	0	0	0	1	1

---

Задание 2.2 Шифрование и дешифрование сообщений методами Цезаря и Виженера

Сутью шифра Цезаря является замена одной буквы другой, находящейся на некоторое постоянное число позиций левее или правее от неё в алфавите.

Шифр Виженера представляет собой усовершенствованную многоалфавитную систему шифрования (или, как её ещё называют, полиалфавитная). Идея шифра состоит в использовании в качестве ключа (кодовое слово) текст самого сообщения (открытого - не зашифрованного) или же шифрованного текста (закрытого). Кроме того, для усиления стойкости шифра, в качестве первого символа ключа берется случайным образом буква из алфавита.

Процесс шифрования осуществляется следующим образом:

1. 
   Под каждой буквой шифруемого текста записываются буквы ключа.
   

Ключ при этом повторяется необходимое число раз.

2. Каждая буква шифруемого текста заменяется по подматрице буквами находящимися на пересечении линий, соединяющих буквы шифруемого текста в первой строке подматрицы и находящимися под ними букв ключа.

3. Полученный текст может разбиваться на группы по несколько знаков.

Пусть, например, требуется зашифровать сообщение: максимально допустимой ценой является пятьсот руб. за штуку.

В соответствии с первым правилом записываем под буквами шифруемого текста буквы ключа. Получаем:

максимально допустимой ценой является пятьсот руб. за штуку

книгакнигак нигакнигак нигак нигакниг акнигак ниг ак нигак

Дальше осуществляется непосредственное шифрование в соответствии со вторым правилом, а именно: берем первую букву шифруемого текста (М) и соответствующую ей букву ключа (К); по букве шифруемого текста (М) входим в рабочую матрицу шифрования и выбираем под ней букву, расположенную в строке, соответствующей букве ключа (К),-- в нашем примере такой буквой является Ч; выбранную таким образом букву помещаем в зашифрованный текст. Эта процедура циклически повторяется до зашифрования всего текста.

Задание. Зашифруйте сообщение, используя шифры Цезаря и Вижинера.

Буквенная таблица представлена в Приложении 2.

Вариант	Сообщение
1	Буря мглою небо кроет, Вихри снежные крутя; То, как зверь, она завоет, То заплачет, как дитя Ключ: Радио
2	Если жизнь тебя обманет, Не печалься, не сердись! В день уныния смирись: День веселья, верь, настанет. Ключ: Солнце
3	Приветствую тебя, пустынный уголок, Приют спокойствия, трудов и вдохновенья, Где льется дней моих невидимый поток На лоне счастья и забвенья. Ключ: Море
4	Во глубине сибирских руд Храните гордое терпенье, Не пропадет ваш скорбный труд И дум высокое стремленье. Ключ: Судья
5	В поле чистом серебрится Снег волнистый и рябой, Светит месяц, тройка мчится По дороге столбовой. Ключ: Книга
6	Великий день Бородина Мы братской тризной поминая, Твердили: "Шли же племена, Бедой России угрожая. Ключ: Крот
7	Умом Россию не понять, аршином общим не измерить, у ней особенная стать — В Россию можно только верить. Ключ: Липа
8	Нам не дано предугадать, как слово наше отзовётся, — и нам сочувствие даётся, как нам даётся благодать… Ключ: Ружьё
9	Роняет лес багряный свой убор, Сребрит мороз увянувшее поле, Проглянет день как будто поневоле И скроется за край окружных гор. Ключ: Весна
10	Роняет лес багряный свой убор, Сребрит мороз увянувшее поле, Проглянет день как будто поневоле И скроется за край окружных гор. Ключ: Лист

---

Задание 2.3 Передача сообщений методами Фано и Хаффмана

Исторически первый код, предназначенный для передачи сообщений, связан с именем изобретателя телеграфного аппарата Сэмюэля Морзе и известен как азбука Морзе. В этом коде каждой букве или цифре сопоставляется своя последовательность из кратковременных (называемых точками) и длительных (тире) импульсов тока, разделяемых паузами. Другой код, столь же распространенный в телеграфии (код Бодо), использует для кодирования два элементарных символа - импульс и паузу, при этом сопоставляемые буквам кодовые слова состоят из пяти таких сигналов.

Общую схему передачи сообщений представлена на рисунке 1.



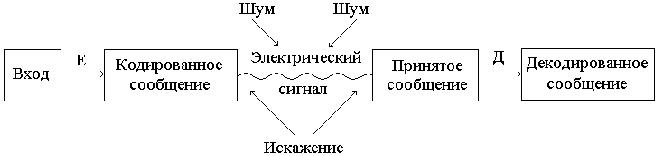
Рис. 1. Схема передачи сообщений

Коды, использующие два различных элементарных сигнала, называются двоичными. Удобно обозначать эти два сигнала 0 и 1. Тогда кодовые слова можно представлять как последовательность из нулей и единиц.

Коды Фано и Хаффмана являются оптимальными и префиксными. При построении искомых кодов применяют как традиционный табличный способ кодирования, так и кодирование с помощью "кодового дерева".

При кодировании по Фано все сообщения записываются в таблицу по степени убывания вероятности и разбиваются на две группы примерно (насколько это возможно) равной вероятности. Соответственно этой процедуре из корня кодового дерева исходят два ребра, которым в качестве весов присваиваются полученные вероятности. Двум образовавшимся вершинам приписывают кодовые символы 0 и 1. Затем каждая из групп вероятностей вновь делится на две подгруппы примерно равной вероятности. В соответствии с этим из каждой вершины 0 и 1 исходят по два ребра с весами, равными вероятностям подгрупп, а вновь образованным вершинам приписывают символы 00 и 01, 10 и 11. В результате многократного повторения процедуры разделения вероятностей и образования вершин приходим к ситуации, когда в качестве веса, приписанного ребру бинарного дерева, выступает вероятность одного из данных сообщений. В этом случае вновь образованная вершина оказывается листом дерева, т.к. процесс деления вероятностей для нее завершен. Задача кодирования считается решенной, когда на всех ветвях кодового бинарного дерева образуются листья.

Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево).

---