Лекциялық сабақтың тақырыбы №2
Тақырыбы: Электр өрісінің кернеулік сызықтары. Кернеулік векторының ағыны.

Электрлік ығысу.Остраградский-Гаусс теоремасы.

Жоспары: 1. Электр өрісінің кернеулік сызықтары.

2. Кернеулік векторының ағыны.

3. Электрлік ығысу.

4. Остроградский-Гаусс теоремасы. Аталған тақырыптарға есептерге талдау жасау, шығару жолдарын талқылау, шешімін табу.

Оқыту нәтижесі:
Практикалық сабақтың мазмұны: Электр өрісін көрнекі түрде кескіндеу. Кеңістікте орналасқан зарядтармен оның айналасында пайда болған электр өрісінің кернеулік векторының арасындағы байланыс заңдылығын көрсету үшін кернеулік векторының ағыны деген ұғым ендірілді. Бізге енді әртекті ортаның шекарасындағы бір нүктенің (мысалы ауа мен судың) кернеулігін анықтау керек . Остроградский – Гаусс теоремасы кез келген тұйық беттен өтетін электрлік ығысу ағынының сол беттің ішіндегі электр зарядының арасындағы байланысты көрсетеді.

Электр өрісінің кернеулік сызықтары. Электр өрісі кернеулігін графикпен кескіндеу үшін, өрістің әр нүктесі арқылы, осы нүктедегі электр өрісі кернеулігінің шамасы мен бағытын көрсететін стрелка жүргізсе болар еді, бірақ өрісті бұлай кескіндеу тиімсіз, өйткені стрелкалар бір-бірімен қабаттасып, түсініксіз суреттер берер еді. Сондықтан ағылшын ғалымы Фарадей өрісті сызықтармен кескіндеуді ұсынды. Ол сызықтардың әр нүктесіндегі жанамалар, сол нүктедегі өрістің кернеулігі (Е) векторымен дәл келетін болу керек. Мұндай сызықтар өрістің күш сызықтары немесе кернеулік сызықтары деп аталады. Күш сызықтары оң зарядтардан басталып, теріс зарядтардан немесе шексіздікте аяқталады деп ұйғарылған. Кернеулік күш сызықтарының өрісте орналасу жилігіне қарап, өріс кернеулігінің шамасын да сипаттауға болады.

Кернеулік векторының ағыны. Кеңістікте орналасқан зарядтармен оның айналасында пайда болған электр өрісінің кернеулік векторының 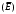арасындағы байланыс заңдылығын көрсету үшін кернеулік векторының ағыны деген ұғым ендірілді.

Кернеулік сызықтарының жиілігі 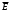-нің сан мәніне тең болсын. Сонда белгілі бір бетті қиып өтетін кернеулік сызықтарының жалпы санын – сол беттен өтетін кернеулік ағыны немесе өрістің кернеулік ағыны деп атайды.

---

Мысалы, біртекті электр өрісінде S жазық бетті қиып өтетін кернеулік векторлар ағынын анықтайық. Электр өрісінің күш сызықтары S бетін перпендикуляр бағытта қиып өтсін, кернеулік сызықтарының S бетке көбейтіндісі – кернеулік векторының ағыны деп аталады, оны Ф - әрпімен белгілейді.

Ф=E·S (1).

Егерде S’ жазық бет өрістің кернеулік сызықтарына белгілі бір бұрышыпен көлбеу орналасса

Ф=E· S’ (2) мұндағы S’=Scos (3)

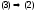Ф=E·S cos (4) мұндағы  - S’ бетке жүргізілген нормальмен кернеулік сызықтары арасындағы бұрыш

Енді өрістің кернеулік сызықтары біртекті емес кез келген тұйық бетті қиып өтсе, онда векторлық ағын



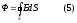
Кернеулік сызықтарының ағыны (Ф) – скаляр шама. Кез келген бағытта орналасқан беттен өтетін кернеуліктің ағыны – кернеуліктің нормаль құраушысы мен ауданының көбейтіндісіне тең. Егер аудан S кернеулік сызықтарына || болса, онда одан өтетін ағын нолге тең болады, бұл жағдайда



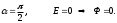
(4) өрнектен ағын сызықтарының оң және теріс таңбалы болатынын байқауға болады.

1) Егер 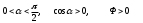болады.

2)

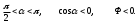
Электрлік ығысу. Бізге енді әртекті ортаның шекарасындағы бір нүктенің (мысалы ауа мен судың) кернеулігін анықтау керек болсын делік. Осы нүкте арқылы электр өрісінің кернеулігі өтетін болса, онда кернеуліктің шамасы мысалы ауа үшін =1, су үшін =81 тең болғандықтан 81 есе кемиді екен. Олай болса, кернеулік векторының ағыны да соншаға азаяды. Сондықтан әр түрлі ортаның шекарасында және диэлектриктерде өтетін кернеулік векторының өзгерістері электр өрістерін анықтап есептеуде көптеген қиындықтар туғызады. Осы қиындықтардан құтылу үшін жаңа векторлық шама ендіруге тура келеді. Оны D әрпімен белгілеп, электрлік ығысу векторы немесе электрлік индукция векторы деп атайды. Бұл вектор электр өрісінің кернеулігі 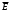- мен қарапайым түрде байланысып, көмекші вектордың ролін атқарады.

Электрлік ығысу векторы сан жағынан кернеулік векторы 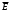-нің обсолюттік, диэлектрлік өтімділікке () көбейтіндісіне тең болады.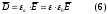



Скаляр түрде: D=

---

₀  E (7)

Егер



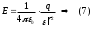
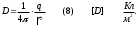
Электрлік ығысу ортаның қасиетіне тәуелсіз екендігін (8)-ші өрнектен көруге болады. Электрлік ығысу векторының өрісін кернеулік 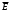векторының графиктері сияқты кескіндеуге болады. Сондай-ақ электрлік ығысу сызықтары деп аталатын өріс сызықтарын алу керек. Берілген бір бетті қиып өтетін электрлік ығысу саны электрлік ығысу векторының ағыны деп аталады. Электрлік ығысу векторының ағыны скаляр шама. Ал кез келген әртекті өрісте белгілі бір S бетті қиып өтетін электрлік ығысу ағыны: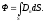



Остроградский – Гаусс теоремасы. О – Гаусс теоремасы кез келген тұйық беттен өтетін электрлік ығысу ағынының сол беттің ішіндегі электр зарядының арасындағы байланысты көрсетеді. Бұл теорема бірте-бірте ең қарапайым нүктелік зарядтың электр өрісін, кез келген бетте таралып орналасқан зарядтар жүйесінің өрістерін қарастырады. Енді біз ортасында q нүктелік заряды бар, радиусы r шар тәрізді сфералық бетті қиып өтіп жатқан кернеулік векторының ағынын анықтайық:



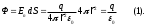
Яғни, тұйықталған беттің пішіні қандай болғанымен де, q нүктелік зарядқа қоршаған осы бетті қиып өтетін 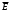векторлар ағы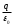н екен.

Егер қандай да бір тұйықталған беттің ішінде әр аттас n заряд болса, онда оның толық ағыны барлық нүктелік зарядтардың 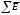қосындысына тең болады: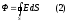



Электр өрісінің суперпозиция принципін ескерсек, яғни



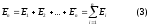
(2), (3) ескерсек, онда



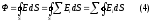
мұндағы 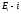зарядтың жеке туғызатын өріс кернеулігінің құраушысы.

(1) ескеретін болсақ,

Осы (5) формула вакуумдағы электростатикалық өріс үшін Гаусс теоремасы болып есептеледі. Бұл теорема былайша тұжырымдалады: тұйықталған бет арқылы өтетін электр өрісі кернеулігінің векторлық ағыны осы беттің ішіндегі зарядтардың алгебралық қосындысы 

---

₀-ге бөлгенге тең.

Осы теореманы кейіндеу математикалық тұрғыдан орыс математигі Острградский М.В. (1801-1862) әртекті өріс кернеулігі үшін қорытып шығарды. Ал Гаусс болса, оны тек электростатикалық өріс үшін ғана дәлелдеді. Егер заряд көлемдік тығыздығы _v болатын тұйықталған беттің ішінде үздіксіз таралса, яғни 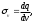онда V көлем ішінде зарядтардың шамасы:

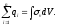Бұдан Гаусс теоремасы

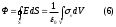болып өрнектеледі.

Гаусс теоремасы көптеген практикалық жағдайларда нүктелік зарядтардың өріс кернеулігін оңай тәсілмен табуға мүмкіндік береді.

Остроградский – Гаусс теоремасынан шығатын тұжырымдар:

- кернеулік сызықтары тек оң зарядтар бар жерлерден басталып, теріс зарядтар бар жерлерде аяқталады;

- алгебралық қосындысы нолге тең зарядтарды қамтитын тұйықталған бетті алсақ, онда сол бет арқылы өтетін кернеулік векторларының толық ағыны нөлге тең, себебі, сол бет қамтитын көлемнен шығатын сызықтардың саны көлемге енетін сызықтардың санына тең;

- тұйықталған бет ішінде зарядтар болмаса, онда кернеулік сызықтары бетті қиып өткенде, оның ішінде басталмайды да, аяқталмайды да. Сондықтан бетке енетін сызықтардың саны шығатын сызықтардың санына тең болады да, толық кернеулік ағыны нөлге айналады.

Өріс кернеуліктерін табу үшін зарядтардың тығыздығы деген ұғым ендіріледі.

Зарядтардың сызықтық тығыздығы деп белгілі бір сызық бойымен немесе жіңішке цилиндр бойында біркелкі орналасқан зарядтардың сол ұзындықтың қатынасына тең болатын физикалық шаманы айтамыз:



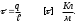
Егер зарядтар белгілі бір бетте орналасса, онда беттік тығыздық:



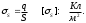
Зарядтар сфералық көлем бойынша орналасса, олардың көлемдік тығыздығы:



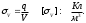
Оқытудың техникалық құралдары: интерактивті тақта, проектор сызба – кестелер, плакаттар.

Оқытудың әдістері мен түрлері:

---

баяндау, сұрақ – жауап, түсіндіру, практикалық сабақтар,топтық жоба жұмыстары , проблемалық оқыту , интербелсенді оқыту.

Деңгейлік тапсырмалар:

1. Электр өрісін графиктік түрде кескіндеу.

2. Кернеулік векторының ағыны.

3. Электрлік ығысу.

4. Остоградский – Гаусс теоремасы

5. Электрлік ығысу векторының ағыны

ОБСӨЖ тапсырмалары: Табиғаттағы электрлік құбылыстар.

СӨЖ тапсырмалары: Электрлік құбылыстардың адамға әсері және олардан қорғану.
Пайдаланылатын әдебиеттер:

Негізгі әдебиеттер:

1. 
   Электромагнетизм: негізгі заңдар. Оқулық. -2013. И. Е. Иродов
   
2. 
   Электромагниттік тербелістер мен толқындар. Оқулық. -2013. М. Құлбекұлы, Ш. Хамраев
   
3. 
   Физика есептерін шығару. 2013. Ә. М. Бектенов, Б. М. Бектенов, М(Л). Б. Бектенов.
   
4. 
   Жалпы физика курсынан зертханалық жұмыстар - ІІ. 2017. Тұрмамбеков Т.А., Сарыбаева Ә.Х., Беркинбаев М.О.
   

Қосымша әдебиеттер:

5. 
   Общая физика (электричество и магнетизм). Учебное пособие. 2014, Антонов
   
6. 
   Электричество и магнетизм. 2011. Д.П. Стрыгин.
   

Web-сайттар:

Электр және магнетизм: Оқу құралы. 2016 http://rmebrk.kz/book/1161804 Айдарбекова, Ж.М.

Электричество и магнетизм. 2011 http://rmebrk.kz/book/1136063 Д.П. Стрыгин

http://rmebrk.kz

library.ayu.edu.kz

https://elib.kz/ru/search/

---

Смотрите также файлы

• Разработка бизнесплана открытия кофейни.ppt

• Эту книгу хорошо дополняют Прибыльная контекстная реклама.pdf

• Ссср в 19451953 гг..doc

• Липиды.docx

• Кафедра общегуманитарных наук и массовых коммуникаций.docx