Министерство образования и науки российской федерации Федеральное государственное бюджетное образовательное учреждение Высшего образования Нижневартовский государственный университет ФАКУЛЬТЕТ ЭКОЛОГИИ И ИНЖИНИРИНГА Кафедра Нефтегазовое дело

Задачи по дисциплине:

«Прикладная механика»
Вариант №3
21.03.01 «Нефтегазовое дело» (ЭОТОНП)

Выполнил: студент группы 9062 заочного отделения Амбарников А.В. Проверил: канд. эконом. наук, доцент Некрасов А.В.

г.Нижневартовск, 2022
Задание 3
Центральное растяжение и сжатие прямых стержней переменного сечения

Для стального ступенчатого стержня, 1 находящегося под действием сил F_i, приложенных в осевом направлении, требуется:

1) построить эпюры нормальных сил N, нормальных напряжений ;

2) построить эпюру осевых перемещений ;

3) определить его полное удлинение (укорочение) l.

Исходные данные

№ п\п	Нагрузка, кН			Площадь сечения А104, м2	Длина участка а, м
	F1,	F2,	F3,
3	10	24	22	10	1,8

Рисунок 3.1

---

Рис.3.1
Решение


1. Разбиваем брус на участки, границами которых являются сечения, где приложены сосредоточенные силы, а также сечения, где меняется площадь. Исходя из этого, разбиваем брус на 3 участка.

В пределах каждого участка проводим произвольные сечения и методом сечений определяем внутренние усилия (продольные силы). На третьем участке проводим сечение 3-3

Рассмотрим равновесие правой отсеченной части. Воздействие левой отброшенной части на правую заменим продольной силой и предварительно направим её от сечения, т.е предположим, что сила является растягивающей. Составим уравнение равновесия.

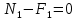, откуда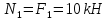

(растяжение).

Аналогично определяем продольные силы на других участках:

,

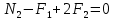откуда

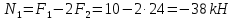
(сжатие).
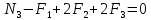, откуда



(сжатие).
По полученным данным строим эпюру продольных сил.

Определим нормальные напряжения на участках:



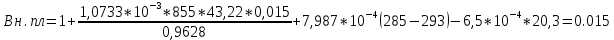
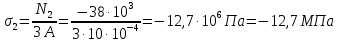
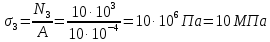
По полученным данным строим эпюру продольных сил.
2. Построить эпюру осевых перемещений ;
Определим деформации участков, используя закон Гука:



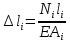
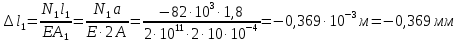
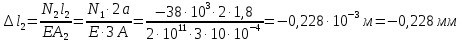
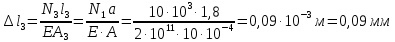
Строим эпюру осевых перемещений, начиная с закрепленного конца стержня:






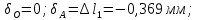
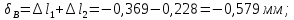
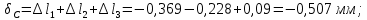
3. Полное укорочение стержня составит




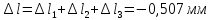
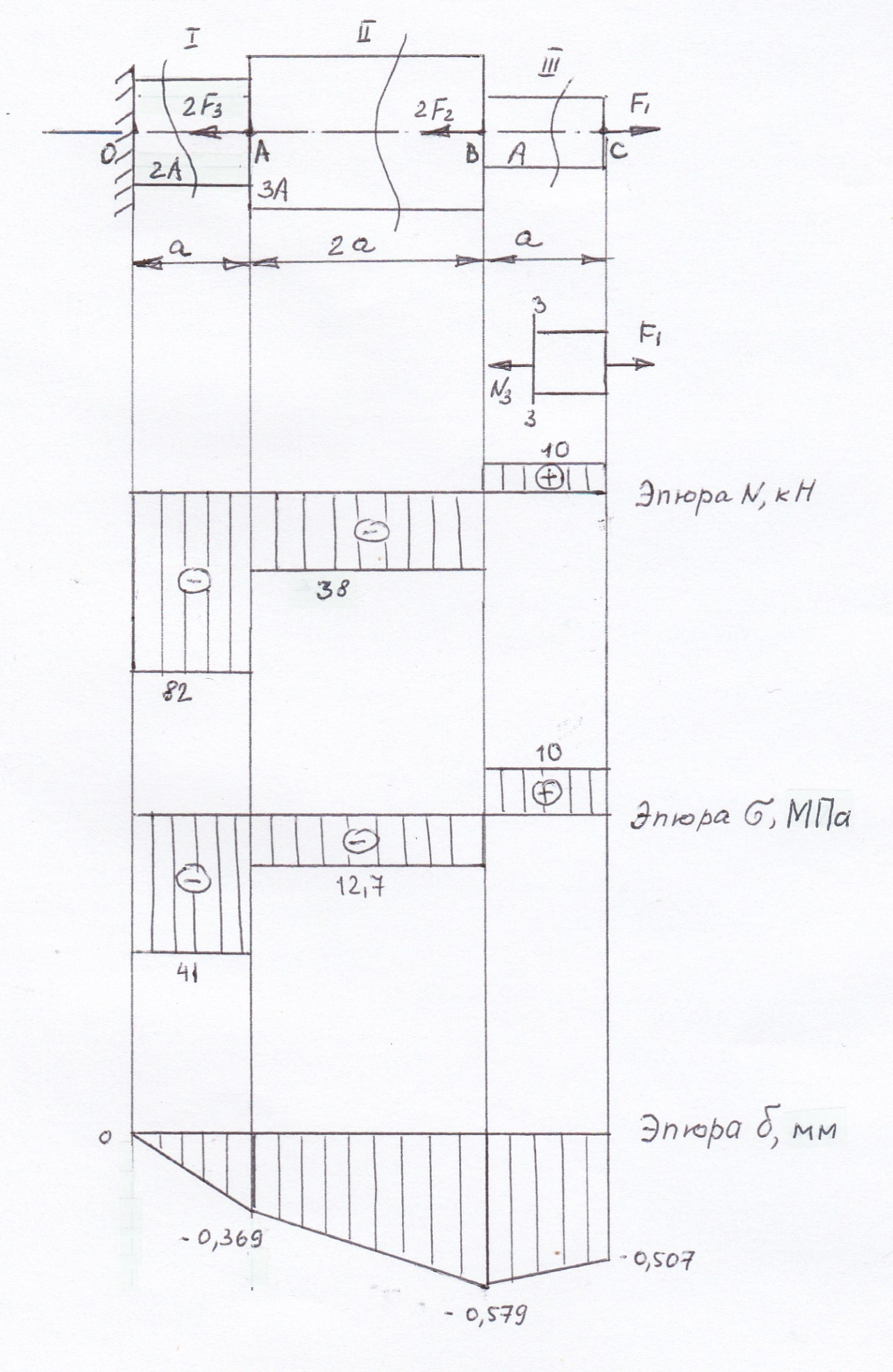
Рис.3.2

---

Задание 4
Расчет на кручение круглых стержней.

Для стального вала, один конец которого условно принят защемленным, при выбранных исходных данных требуется:

1) найти через известные мощности P_i соответствующие скручивающие моменты m_i;

2) найти неизвестный момент m₄ из условия равенства нулю угла поворота свободного конца вала;

3) построить эпюру крутящих моментов T;

4) подобрать круглое и кольцевое (при заданном =d/D) сечения из условий прочности;

5) построить эпюры углов поворота  по длине вала круглого сечения;

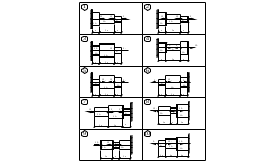
Исходные данные в таблице 4.


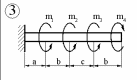
Рис.4.1

№ п\п	Мощность, кВт			Длины участков, м			Угловая скорость , рад/с рад\с		=d/D		Допускаемые напряжения, , МПа		Допускаемый угол закручивания, , град\м
	P1	P2	P3	a	b	c
3	90	40	60	0,5	0,3	0,6		28		0,9		30		0,45

Решение

1. 
   Определяем скручивающие моменты:
   

;

;

.

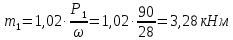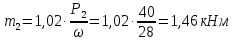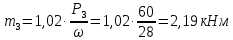2 Значение неизвестного момента m₄ найдем из того условия, что угол закручивания свободного конца вала равен нулю, т.е. _А=0. Для удобства счета разобьем этот угол на составляющие, зависящие от каждого скручивающего момента, т.е. φ_А = φ_тА⁺ φ_mА⁺ φ_т2⁺ φ_m3= 0 ,

где φ_тА

---

- угол поворота концевого сечения от действия только момента т_a,φ_m1- то же, но от действия только момента m₁;

φ_m2 - от действия только момента т₂; φ_т3 - от действия только момента m₃;

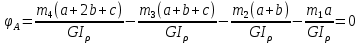
Подставив числовые значения, после преобразований, получим:

3. 
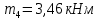
   Пользуясь методом сечений, определяем величины крутящих моментов на отдельных участках вала.
   

Участок 1

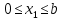
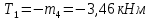
Участок 2

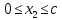
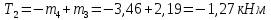
Участок 3

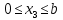
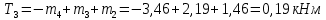
Участок 4

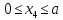
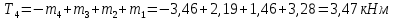
По полученным значениям крутящих моментов строим эпюру Т (рис. 4.2,б).

4. По условию прочности вала



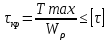
Найдем требуемое значение полярного момента сопротивления сечения


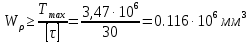
Для сплошного сечения вала:

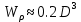, тогда диаметр вала: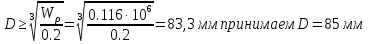

Для кольцевого сечения вала при α=d/D=0.9:
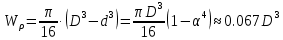тогда диаметр вала: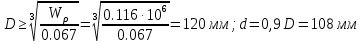


5. Вычислим углы поворота «» для круглого сечения вала:

Полярный момент инерции :

---

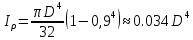
Жесткость сечения:

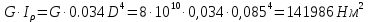
Углы закручивания участков:











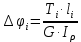
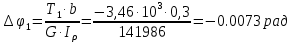
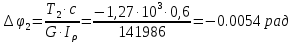
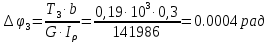
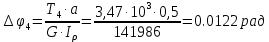
Углы поворота сечений:





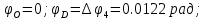
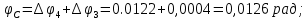
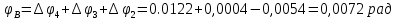
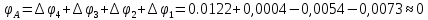
По полученным значениям  строим эпюру углов поворота «» (рисунок 4.2в).



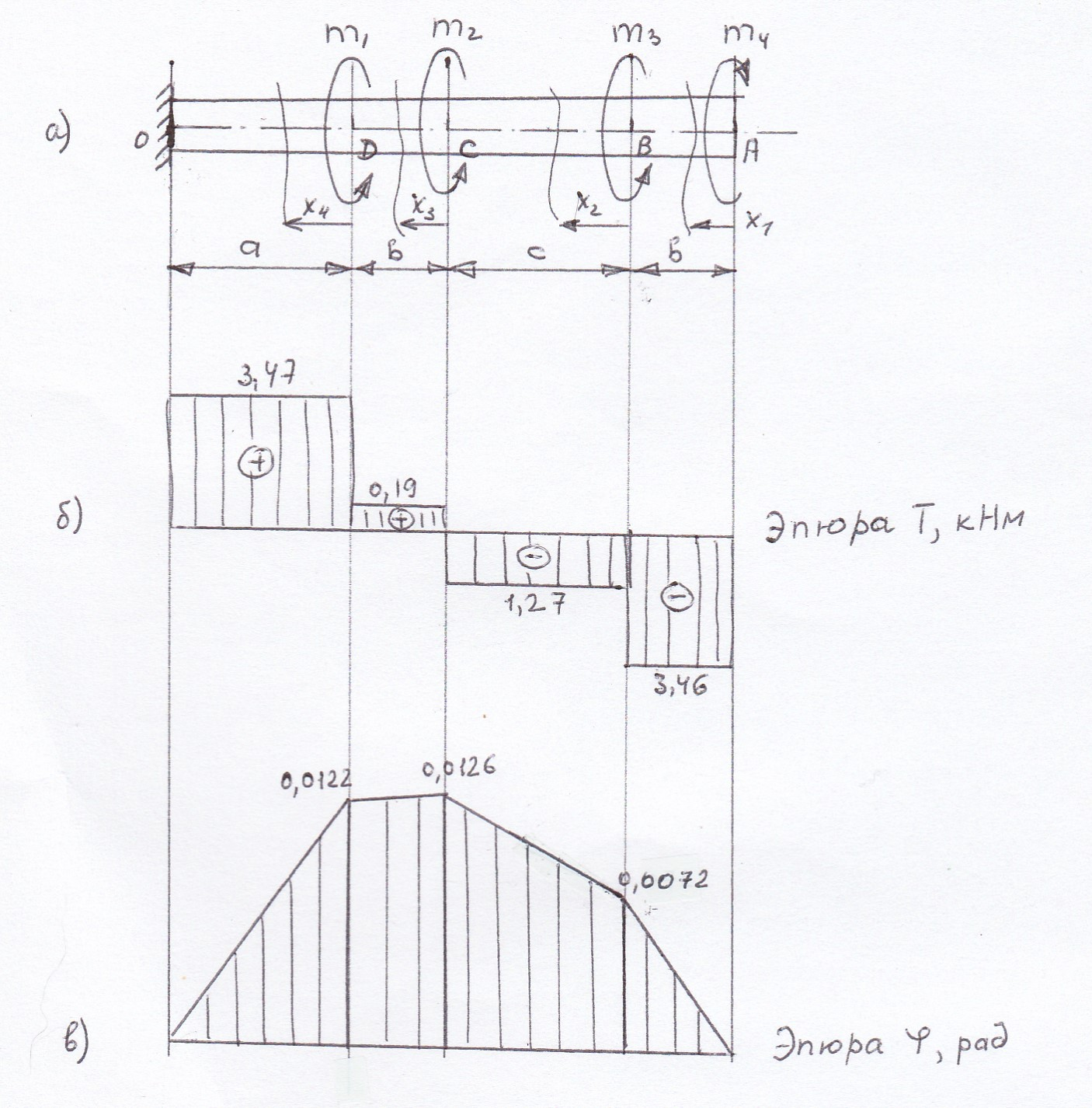
Рис.4.2

Задание 5
Плоский изгиб балочных систем.

Для заданной балки (рисунок 5.1) требуется:

1) построить эпюры поперечных сил Q, изгибающих моментов М;

2) подобрать;

- для балок с 1 по 6 схемы – из сортамента двутавровое сечение, материал балки – сталь []=160 МПа;

Исходные данные в таблице 5



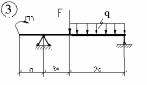
Рис.5.1

Таблица 5

№ п\п	Нагрузка			Длины участков, м
	F, кН	m, кНм	q, кН/м	a	b	c
3	40	40	30	3	3	2

Решение:

1 Определим опорные реакции

1. Определение опорных реакций.

Из условия статического равновесия балки на двух опорах найдем (рис. 5.2а):







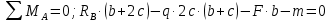
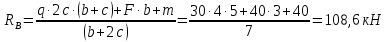
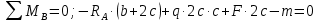
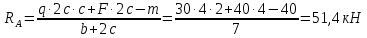
Проверка:

---

Смотрите также файлы

• Суд по гражданским делам г.docx

• Тэк рф проблемы собственности и государственного регулирования 6.docx

• Контрольная работа дисциплина Основы маркетинга Ф. И. О студента Хорольская Кристина Станиславовна Социология экономики и маркетинга.docx

• Модуль инструменты поддержки экспорта экспортная страховая компания KazakhExport.pdf

• Классный час викторина на тему "Правила дорожного движения".docx