ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.03.2024
Просмотров: 29
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
показатель, характеризующий среднюю абсолютную скорость роста (или снижения) уровня за отдельные периоды времени
разница между третьим квартилем и первым квартилем набора данных относительный показатель, характеризующий интенсивность процесса роста.
- Определенный интеграл применяется тогда, когда мы ...
собираемся найти площадь под кривой собираемся найти ошибку прогноза
собираемся найти скорость максимального изменения функции
- Плотность вероятности - это ...
статистический показатель, отражающий взаимосвязи, которые объективно существуют между явлениями.
это обобщенная количественная характеристика признака в статистической совокупности в конкретных условиях места и времени.
скорость изменения функции распределения
-
Производная функция – это ... скорость изменения функции в данной точке составляющая переменной
соблюдение размещения
-
 Что из нижеперечисленного является формулой теоремы Муавра — Лапласа?
Что из нижеперечисленного является формулой теоремы Муавра — Лапласа?
А Б
В
- Размещение – это …
упорядоченный набор чисел из некоторого множества различных n элементов упорядоченный набор из k различных элементов из некоторого множества
различных n элементов
упорядоченный набор из k различных элементов из суммы различных n элементов
- Размещение без повторений – это размещение, где …
элементы повторяются элементы не повторяются
элементы могут повторяться и не повторяться
- Распределение вероятности - это
закон описывающий область значений случайной величины и соответствующие вероятности проявления этих значений
представляет собой разность между максимальным и минимальным значениями признака.
относительный показатель, который выражает соотношение величин какого-либо явления во времени, в пространстве или сравнение фактических данных с любым эталоном
- Сочетание – это …
неупорядоченный набор из k различных элементов из некоторого множества различных n элементов
упорядоченный набор из k различных элементов из некоторого множества различных n элементов
неупорядоченный набор из чисел из некоторого множества различных n элементов
-
Сочетание без повторений – это … сочетание, где элементы повторяются сочетание, где элементы не повторяются
сочетание, где элементы могут повторяться и не повторяться
-
Сочетания с повторениями – это … сочетания, где элементы могут повторяться сочетания, где элементы могут не повторяться
сочетания, где элементы могут повторяться и не повторяться
- Теорема Муавра – Лапласа в теории вероятностей утверждает, что число успехов при многократном повторении одного и того же случайного эксперимента с двумя возможными исходами …
приблизительно имеет нормальное распределение
подвергается неточности при распределении
имеет точную взаимосвязь событий при распределении
- Теорема Пуассона — пусть есть последовательность серий испытаний Бернулли, ρₙ — вероятность «успеха», а μₙ — …
вероятность события количество «успехов» элементарное событие
- Условная вероятность – это
вероятность наступления двух событий при условии наступлении последующего события
вероятность, где события могут повторяться
вероятность наступления одного события при условии наступлении второго
- Частная производная – это производная ...
по одной переменной в случае, если функция имеет несколько переменных скорость изменения функции в данной точке
грамотное сопоставление условий для решения задачи
- Что из ниже перечисленного является формулой реккурентного соотношения при n, k = 0?
s(0,1)= c(0,0)=1
s(0,0)= c(1,0)=1
s(0,0)= c(0,0)=1
- Числа Стирлинга первого рода (без знака) – это …
количество значений порядка n
количество перестановок значений с k циклами количество перестановок порядка n с k циклами
- Градиентный спуск это ...
строгий порядок разбора всех случаев, возможных решений
Процесс, закономерность, вычисление и т.п., подверженных действию случайных факторов.
метод нахождения локального минимума
или максимума функции
- Числа Стирлинга первого рода (со знаком) s (n, k) – это …
коэффициенты элементов коэффициенты многочлена коэффициенты значений
- Что из ниже перечисленного обозначает символ Похгаммера?
(x)_n
〖(x)〗_n^k (x)_n^(-1)
- Что из ниже перечисленного является формулой размещения с повторениями?
A_n^(-k)=n^k A_n=n^k A_n^(-k)=n
- Что из ниже перечисленного является формулой реккурентного соотношения при n>0 ?
s(n,0)= c(n,0)=0
s(n,0)= c(0,0)=0
s(0,n)= c(0,n)=0
- Что из нижеперечисленного является формулой теоремы Пуассона?
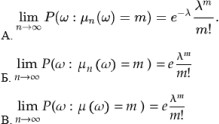
А Б В
- Что из ниже перечисленного является формулой сочетания без повторений?
(n/k)=C_n^k= n!/k!(n-k)!
(n/k)=C_n= n!/k!(n-k)!
(n/k)=C_n^k= n!/(n-k)!
- Что из ниже перечисленного является формулой реккурентного соотношения при k>0 ?
s(k,0)= c(0,0)=0
s(0,k)= c(0,k)=0
s(k,0)= c(k,0)=0
- Что из ниже перечисленного является формулой сочетания с повторениями?
-/(〖 C〗_n^k )= (n+k-1)!/(n-1)!
-/(〖 C〗_n^k )= (n+k-1)!/(k! ∙ (n-1)!)
〖 C〗_n^k= (n+k- )!/(k! ∙ (n-1)!)
- Что из ниже перечисленного является формулой числа Стирлинга первого рода (со знаком)?
(x)_n=(x-1)(x-2) ∙ ∙ ∙ (x-n+1)
(x)_n=x(x-1)(x-2) ∙ ∙ ∙ (x-n)
(x)_n=x(x-1)(x-2) ∙ ∙ ∙ (x-n+1)
- Что из нижеперечисленного является верным суждением условной вероятности?
Вероятность A при условии B, не равна вероятности B при условии A. Вероятность B при условии A, равна вероятности A при условии B. Вероятность A при условии B, равна вероятности B при условии A.
- Что из нижеперечисленного является формулой Бернулли?

А Б В
- Что из ниже перечисленного является формулой числа Стирлинга второго рода?
(n,k)= /k! (j=0)^k 〖(-1)〗^(k+j) (k/j)
(n,k)= /k! (j=0)^k 〖(-1)〗^(k+j) (k/j) j^n
S(n,k)= (j=0)^k 〖(-1)〗^(k+j) (k/j) j^n
- Что из нижеперечисленного является формулой геометрического определения вероятности?
Pr= s/S
Pr (A)= s/S Pr(A) = S
- Что из нижеперечисленного является формулой геометрической вероятности?
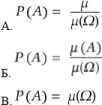
А Б В
- Что из нижеперечисленного является формулой дифференцированного произведения?
(uv)^'=u'v+uv'
(uv)^'=uv+uv' (uv)^'=uv+uv
- Что из нижеперечисленного является формулой дискретного вероятностного пространства?

А Б В
- Что из нижеперечисленного является формулой нахождения градиента?
grad z= dz/dy i +dy/dx j =(dz/dx; dz/dy) grad z= dz/dx i +dz/dx j =(dz/dx; dz/dy) grad z= dy/dx i +dx/dx j =(dz/dx;
