ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.03.2024
Просмотров: 6
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Дата: Класс: 9 | |||
| Тема: Осевая и центральная симметрии | |||
| Цель урока: повторение с учащимися понятий центральной и осевой симметрии, ознакомление с правилами построения симметричных фигур; закрепление знаний на практике; Задачи:
Тип урока: комбинированный. Оборудование: использование компьютерной программы Microsoft Рaint, Power Point, видео и компьютерная техника, компьютерные программы по математике: «GeoGebra», «Живая геометрия», «Свободная плоскость», листы А4 с заданиями, карточки с заданиями, оценочный лист, разноцветные стикеры. Межпредметные связи: русский язык, искусство, биология, спорт, физика, химия. Ведущая технология обучения: технология развития критического мышления, компьютерная технология. «Симметрия… есть идеал, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство» Герман Вейлю | |||
| | Деятельность учителя | Деятельность обучающихся | Наглядности |
| 3 мин. | I. Организационный момент. Приветствует учеников. Сведения об отсутвующих. Для создания психологической атмосферы проводит стратегию Дерево достижений - Обратите внимание на наше одинокое дерево. У каждого из вас есть листочки разного цвета. Я попрошу вас взять один из них (любого цвета) и помочь нашему дереву покрыться разноцветной листвой. Тех, кто выбрал зеленый лист, желают добиться успеха на сегодняшнем уроке и приложат для этого все усилия. Те, кто выбрал Оранжевый, — желают общаться. Желтый — проявят активность. Розовый — будут настойчивы. Помните, что красота дерева зависит от вас, ваших стремлений и ожиданий! | Ученики листочки и вывешивают их на макет дерева. | Макет, дерева, цветные стикеры |
| 10 мин. | II. Проверка пройденного материала. По стратегии «Эврика» проверяет домашнюю работу. Тема урока дается после стратегии, когда они сами смогут ее сформулировать и поставить цели на урок.  | Демонстрируют свои знания, приобретенные в ходе выполнения домашней работы. Осмысливают поставленную цель. | слайд |
| 20 мин. | III. Изучение новой темы 3 этапа 1. Программа «GeoGebra». Показывает осевую и центральную симметрии на примере треугольника.
  2. Программа «Живая геометрия». Показывает пошаговое построение осевой и центральной симметрии на примере треугольника.
Построить симметрию произвольного четырехугольника. 1 вариант – осевую; 2 ариант – центральную. 3. Программа «Свободная плоскость». Показывает и объясняет пошаговое построение осевой и центральной симметрии, используя только угольник (без делений) и циркуль на примере треугольника. В ходе объясняения задет наводящие вопросы классу. | Работая в парах, выполняют построения симметрий фигур в программе Работая индивидуально, ученики изучают новый материал и осваивают пошаговое построение симметрий фигур. Участвуют в построении симметрий, отвечают на вопросы и задают свои. | Прог-рамма «GeoGebra» Прог-рамма «Живая геомет-рия» Прог-рамма «Сво-бодная плос-кость» |
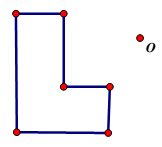
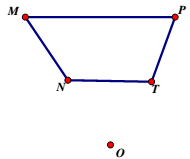
| | IV. Практическая работа №1. Выполняется на листах А4 с помощью угольника и циркуля. На листах готовые чертежи различных геометрически фигур, прямая l и точка О. | С помощью угольника и циркуля выполняют построение симметрий готовых фигур | Уголь-ника, цирку-ли, листы А4 с готовы-ми даны-ми |
| | V. Разминка (психологическая разгрузка) – «Подари комплимент!» - А что вам больше понравилось: дарить комплименты или получать их? | По очереди по цепочке говорят друг другу комплименты. Отвечают на вопрос | Тихая музыка, слайд |
| | VI. Практическая работа №2. 1. Симметрия графиков функций. - Ребята, а вспомните какие графики функций и какой симметрией обладают? (осевая – парабола, многие функции в модуле, центральная куб. парабола, гипербола, и прямая, проходящая через начало координат) 2. Симметрия геометрических фигур. - Симметрией обладают и геометрические фигуры. Например, у прямоугольника две оси симметрии и он имеет центр симметрии, а у круга их бесконечное множество и он также имеет центр симметрии. А произвольный треугольник не имеет симметрии вообще. - 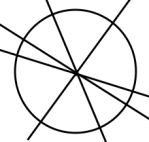 Если геометрическая фигура обладает симметрией, то это значит, что каждая ее точка переходит в симметричную точку этой же фигуры.  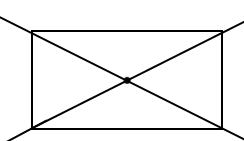Задание: Определить фигуры:
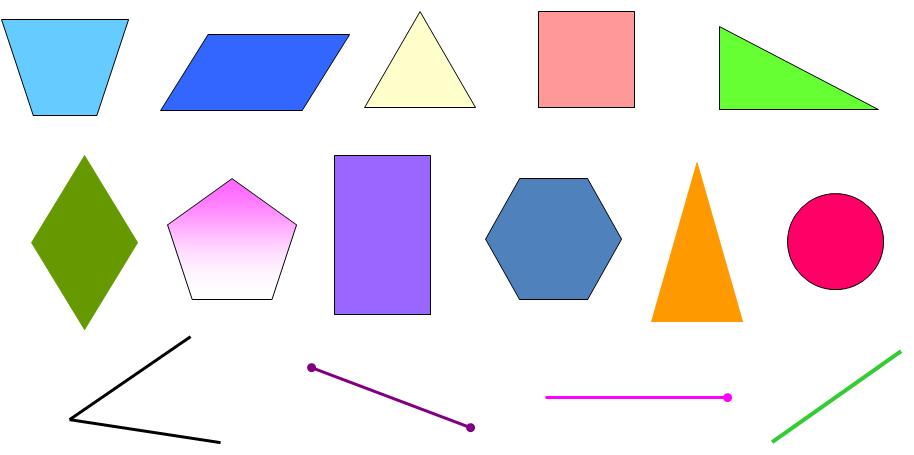 Ответы: 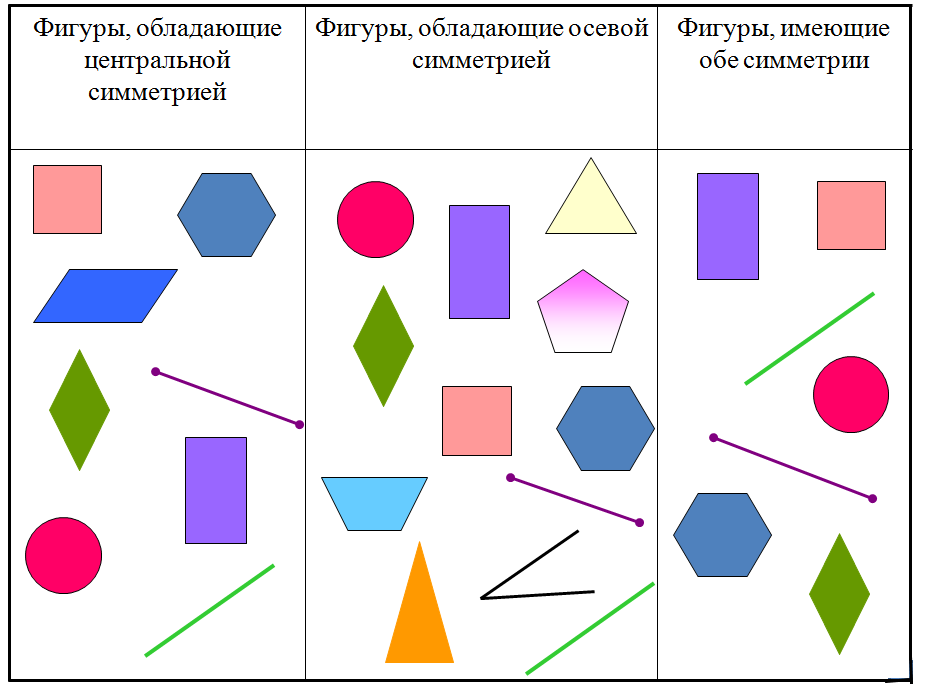 А теперь, устно определим, сколько осей имеет каждая из этих фигур! 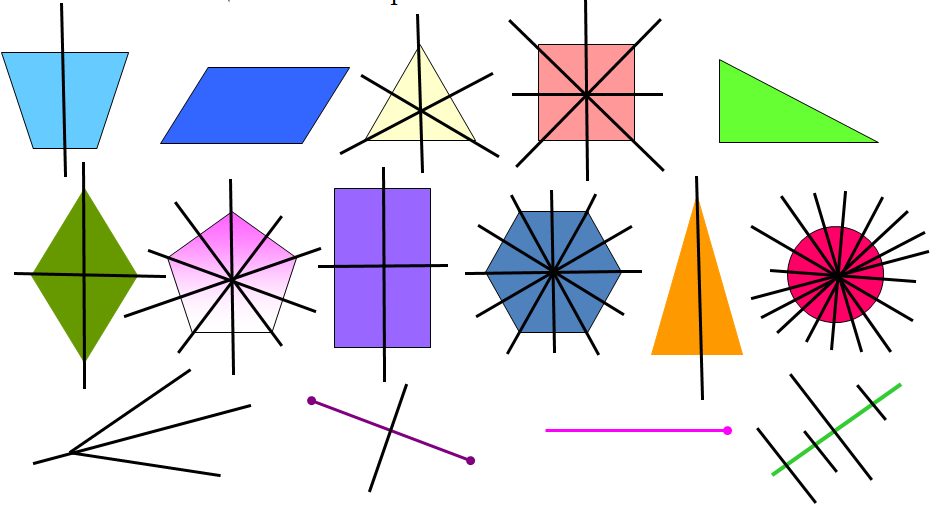 | | Слайды Слайды, бланки для ответов |
| | VII. Домашнее задание.
| Записывают домашнюю работу в дневниках | слайд |
| | VIII. Итог урока. Рефлексия. -Ребята, а достигли ли мы поставленной цели урока? Что нового мы сегодня узнали и чему научились? -А как вы думаете где применяется и встречается симметрия, кроме урока математики? «Симметрия вокруг нас»
| Отвечают на вопросы, комментируют слайды | слайды |
адает задания для практической работы в парах.Итог урока:___________________________________________________________________
_____________________________________________________________________________
Положительные стороны урока:__________________________________________________
_____________________________________________________________________________
Отрицательные стороны урока:___________________________________________________
_____________________________________________________________________________
