Файл: Лабораторная работа 1 по теме Методы решения нелинейных уравнений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.03.2024
Просмотров: 23
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
выберем начальное приближение к корню:  .
.
Для получения решения уравнения методом Ньютона воспользуемся следующей рекуррентной формулой:
В нашем случае
В сценарии пакета Scilab создать функцию, реализующую метод итераций, предусмотрев вывод данных, требуемый для заполнения следующей таблицы.
Оценим погрешность после трех итераций по формуле:
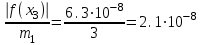 , где
, где 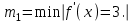
Метод хорд
1. Исследование задания
Проверка выполнения условий сходимости. Для сходимости метода необходимо знакопостоянство на отрезке [a;b].
на отрезке [a;b].
Выбор начального приближения. Вид рекуррентной формулы зависит от того, какая из точек a или b является неподвижной. Неподвижен тот конец отрезка [a;b
] , для которого знак функции f(x)совпадает со знаком ее второй производной. Тогда второй конец отрезка можно принять за начальное приближение к корню, то есть точку х0.
Рекуррентная формула метода хорд в [1]:
 где
где  - неподвижная точка.
- неподвижная точка.
Выше было показано, что для функции f(x)=1–3x+cosx <0 на отрезке [0;1]неподвижной точкой является точка x=b=1, так как
<0 на отрезке [0;1]неподвижной точкой является точка x=b=1, так как  f(1)>0.
f(1)>0.
Таким образом, полагая x0=a=0, получим сходящуюся последовательность приближений к корню.
В рассматриваемой задаче рекуррентная формула принимает следующий вид

2. Расчет трех итераций
Для получения решения уравнения методом хорд воспользуемся следующей рекуррентной формулой:

В сценарии пакета Scilab создать функцию, реализующую метод итераций, предусмотрев вывод данных, требуемый для заполнения следующей таблицы.
Оценим погрешность после трех итераций по формуле:
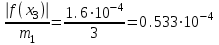

Контрольные вопросы по теме
1. Что является корнем нелинейного уравнения f(x)=0?
2. Чему равна функция в точке корня?
3. Каково условие существования на отрезке [a;b] хотя бы одного корня?
4. При каких условиях корень xбудет единственным на отрезке [a;b]?
5. Из каких этапов состоит процесс решения нелинейного уравнения?
6. В чем заключается этап «отделения корней» нелинейного уравнения?
7. Какие методы используются на этапе отделения корней?
8. Что необходимо, чтобы выбрать x0 в качестве начального приближения в методе Ньютона?
9. Какой метод решения нелинейного уравнения требует более близкого к корню начального значения?
10. Какой метод представляет собой метод решения нелинейного уравнения, в результате которого получается последовательность вложенных отрезков?
11. Можно ли уточнить корень уравнения графическим методом?
12. Что является первым приближением к корню, отделенному на отрезке [a;b],при решении нелинейного уравнения методом половинного деления?
13. Каково правило выбора итерирующей функции при использовании метода итераций?
14. Что принимается за начальное приближение в методе итерации?
15. Каково правило выбора неподвижной точки при использовании метода хорд?
16. Какое значение выбирается в качестве начального приближения в методе хорд?
17. Для каких функций не рекомендуется применять метод Ньютона?
18. Можно ли применять метод итераций, если на заданном отрезке имеются два корня?
19. Какой метод решения нелинейного уравнения обладает свойством «самокоррекции»?
20. Что относится к способам улучшения сходимости метода простой итерации? 0>0>0>
Для получения решения уравнения методом Ньютона воспользуемся следующей рекуррентной формулой:
В нашем случае
-
Расчет трех итераций
В сценарии пакета Scilab создать функцию, реализующую метод итераций, предусмотрев вывод данных, требуемый для заполнения следующей таблицы.
| // Метод Ньютона function ff=f(x) //левая часть уравнения ff=1-3*x+cos(x); endfunction function ff=f1(x) // первая производная от f(x) ff=-3-sin(x); endfunction // Расчет 3-х итераций по методу итераций disp(' n x f(x)') n=0; x=0; fx=f(x); z=[n,x,fx]; z for n=1:3 x=x-f(x)/f1(x); fx=f(x); z=[n,x,fx] end --> x=0; --> exec('nuton.sce',0); n x f(x) z = 0. 0. 2. z = 1. 0.66667 -0.21411 z = 2. 0.60749 -0.0014 z = 3. 0.6071 -6.3D-08 |
| k | Xk | f(xk) |
| 0 | 0 | 2 |
| 1 | 0.62001 | -0.21411 |
| 2 | 0.60712 | -0. 0014 |
| 3 | 0.60710 | -6.3 •10-8 |
-
Погрешность численного решения нелинейных уравнений
Оценим погрешность после трех итераций по формуле:
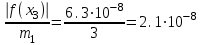 , где
, где 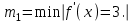
Метод хорд
1. Исследование задания
Проверка выполнения условий сходимости. Для сходимости метода необходимо знакопостоянство
Выбор начального приближения. Вид рекуррентной формулы зависит от того, какая из точек a или b является неподвижной. Неподвижен тот конец отрезка [a;b
] , для которого знак функции f(x)совпадает со знаком ее второй производной. Тогда второй конец отрезка можно принять за начальное приближение к корню, то есть точку х0.
Рекуррентная формула метода хорд в [1]:
 где
где Выше было показано, что для функции f(x)=1–3x+cosx
Таким образом, полагая x0=a=0, получим сходящуюся последовательность приближений к корню.
В рассматриваемой задаче рекуррентная формула принимает следующий вид
2. Расчет трех итераций
Для получения решения уравнения методом хорд воспользуемся следующей рекуррентной формулой:
В сценарии пакета Scilab создать функцию, реализующую метод итераций, предусмотрев вывод данных, требуемый для заполнения следующей таблицы.
| // Метод хорд functionff=f(x) //Левая часть уравнения ff=1-3*x+cos(x); endfunction // Расчет 3-х итераций по методу итераций disp(' n x f(x)') n=0; x=0; fx=f(x); z=[n,x,fx]; z for n=1:3 x=x-f(x)/(f(xx)-f(x))*(xx-x); fx=f(x); z=[n,x,fx] end --> xx=1; --> exec('xord.sce',0); n x f(x) z = 0. 0. 2. z = 1. 0.57809 0.10325 z = 2. 0.60596 0.00408 z = 3. 0.60706 0.00016 |
| n | Xn | f(xn) |
| 0 | 0 | 2 |
| 1 | 0.5781 | 0.10325 |
| 2 | 0.6441 | 0.00408 |
| 3 | 0.6070 | 0.00016 |
-
Погрешность численного решения нелинейных уравнений
Оценим погрешность после трех итераций по формуле:
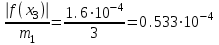
-
Решение нелинейного уравнения с использованием функции пакета Scilab fsolve
| -->deff('y=f(x)','y=1-3*x+cos(x)'); --> [x,fx]=fsolve(0,f) fx = 1.110D-16 x = 0.6071016 |
Контрольные вопросы по теме
«Методы решения нелинейных уравнений»
1. Что является корнем нелинейного уравнения f(x)=0?
2. Чему равна функция в точке корня?
3. Каково условие существования на отрезке [a;b] хотя бы одного корня?
4. При каких условиях корень xбудет единственным на отрезке [a;b]?
5. Из каких этапов состоит процесс решения нелинейного уравнения?
6. В чем заключается этап «отделения корней» нелинейного уравнения?
7. Какие методы используются на этапе отделения корней?
8. Что необходимо, чтобы выбрать x0 в качестве начального приближения в методе Ньютона?
9. Какой метод решения нелинейного уравнения требует более близкого к корню начального значения?
10. Какой метод представляет собой метод решения нелинейного уравнения, в результате которого получается последовательность вложенных отрезков?
11. Можно ли уточнить корень уравнения графическим методом?
12. Что является первым приближением к корню, отделенному на отрезке [a;b],при решении нелинейного уравнения методом половинного деления?
13. Каково правило выбора итерирующей функции при использовании метода итераций?
14. Что принимается за начальное приближение в методе итерации?
15. Каково правило выбора неподвижной точки при использовании метода хорд?
16. Какое значение выбирается в качестве начального приближения в методе хорд?
17. Для каких функций не рекомендуется применять метод Ньютона?
18. Можно ли применять метод итераций, если на заданном отрезке имеются два корня?
19. Какой метод решения нелинейного уравнения обладает свойством «самокоррекции»?
20. Что относится к способам улучшения сходимости метода простой итерации? 0>0>0>
