Томский межвузовский центр дистанционного образования
Томский государственный университет

систем управления и радиоэлектроники (ТУСУР)


Кафедра автоматизированных систем управления

Лабораторная работа №1
по дисциплине «Основы теории управления»


Выполнил:

студент ТМЦДО

специальности 220400

2008 г.

1. 
   ЦЕЛЬ РАБОТЫ
   

Изучение моделей и характеристик основных типовых динамических звеньев систем управления.

2. 
   ХОД РАБОТЫ
   

Выведем выражения передаточных функций для каждого типового звена, в соответствии с его параметрами, хранящимися в таблице.




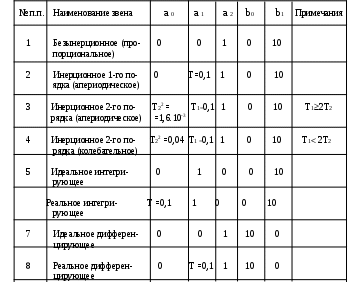
1) W(s) = 10

2) W(s) = 10/(1+0.1s)

3) W(s) = 10/(1+0.1s+0.0016s²)

4) W(s) = 10/(1+0.1 s²+0.004 s²)

5) W(s) = 10/s

6) W(s) = 10/(s+0.1 s²)

7) W(s) = 10s

8) W(s)=10s/(1+0.1s)
Для каждого звена по его передаточной функции запишу операторное уравнение.

1) y=10x

2) (1+0.1s)y=10x

3) (1+0.1s+0.0016s²)y=10x

4) (1+0.1 s²+0.004 s²)y=10x

5) sy=10x

6) (s+0.1 s²)y=10x

7) y=10sx

8) (1+0.1s)y=10sx

Отредактируем модель звена и проведу анализ характеристик во временной и частотной области.

Отличительные особенности переходных функции:

1) Безынерционное звено.

Переходная функция – ступенчатая. АФХ представляет точку на вещественной оси на расстоянии k от начала координат. Модуль частной передаточной функции A(ω)=k и сохраняется на всех частотах. Фазовый сдвиг равен 0.

2) Инерционное звено первого порядка (апериодическое).

Переходная функция – экспонента. На асимптоте касательной, проведенной к

---

кривой в любой точке отсекается отрезок, равен постоянной времени Т. Чем больше значение времени (Т) звена, тем дольше длится переходной процесс. Для положительных частот АФХ имеет вид полуокружности с диаметром k.

3) Инерционное звено второго порядка (апериодическое).

Представляет два инерционных звена 1-го порядка, включенных последовательно друг за другом, с постоянным временем Т₁ и Т₂ и общим коэффициентом k.

4) Инерционное звено второго порядка (колебательное).

Описывается тем же дифференциальным уравнением, что и апериодическое звено, корни характеристического уравнения – комплексные. При Т₁ < 2Т₂ АЧХ имеет резонансный пик, высота которого обротано пропорциональна параметру затухания

5) Идеальное интегрирующее звено.

Сила сигнала увеличивается с уменьшением частоты. Модуль частотной передаточной функции стремится к бесконечности, при ω = 0. АФХ для положительных частот сливается с отрицательной частью мнимой оси. ЛАХ представляет собой прямую с отрицательным наклоном 20 дб/дек, пересекающую ось 0 дб при частоте среза равной k. ЛФХ представляет собой прямую, параллельную оси частот.

6)Реальное интегрирующее звено.

Переходная функция – экспонента. График АФХ – парабола.

7)Идеальное дифференцирующее звено.

ЛАЧХ - прямая с положительным углом наклона.

8)Реальное дифференцирующее звено.

АЧХ имеет иной вид, чем у АЧХ идеального звена. Характеристики совпадают в области низких частот, в области высоких частот наблюдается ослабление сигнала. Коэффициент передачи стремится к значению k/T, при ω стремящейся к бесконечности. На низких частотах фазовые сдвиги, вносимые звеном, являются наибольшими. На высоких частотах фазовый сдвиг уменьшается и стремится к нулю в пределе.
Определим частоты сопряжения и среза для инерционных звеньев, по логарифмическим частотным характеристикам.

Для определения значение частоты сопряжения построю две асимптоты. Перпендикуляр, опущенный из точки их пересечения – есть частота сопряжения.

(частота, при которой процесс выходит из стационарного режима)

Для определения значения частоты среза, необходимо найти точку пересечения графика ЛАЧХ с осью абсцисс.

---

(частоты, при которой происходит срыв)
Инерционное звено первого порядка: ω_сопр = 5,642 рад/с; ω_ср = 98,86 рад/с

Инерционное звено второго порядка (апериодическое): ω_сопр = 20,89 рад/с; ω_ср = 70,79 рад/с

Инерционное звено второго порядка (колебательное): ω_сопр = 4,786 рад/с; ω_ср = 16,6 рад/с
Определю значения полюсов и нулей передаточных функций, и оценю их влияние на характер переходного процесса.

Используя графики определю значения полюсов и нулей.

Инерциальное звено первого порядка (апериодическое) полюс: -10.

Инерциальное звено второго порядка (апериодическое) полюс: -50 и -12.5.

Инерциальное звено второго порядка (колебательное) полюс: -1.25+4.841i и -1.25-4.841i.

Идеальное интегрирующее звено полюс: 0.

Реальное интегрирующее звено полюс: 0.

Идеальное дифференцирующее звено ноль: 0.

Реальное дифференцирующее звено ноль: 0 , полюс: -10.

В случае если нули расположены в области полюсов, происходит увеличение амплитуд собственных колебаний в переходном процессе.

В случае если полюсы удалены друг от друга, происходит уменьшение отклонения в переходном процессе.
Оценю влияние параметра k на переходный процесс, при увеличении значения параметра в два раза.

При увеличении параметра k происходит изменение наклона графиков

Коэффициент передачи определяет наклон линейной статистической характеристики звена.

3. 
   ВЫВОД:
   

В ходе проделанной работы были изучены модели и характеристики основных типовых динамических звеньев систем управления. Выяснилось, что типовые динамические звенья действительно основные составные частями алгоритмических структур систем управления.
КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. 
   Что такое передаточная функция элемента?
   

Передаточная функция линейной системы автоматического управления (САУ) в общем случае определяется формулой . Для стационарного случая . Поэтому передаточной функцией стационарной линейной системы называется множитель

---

, на который умножается показательная функция , проходя через эту систему. Передаточная функция стационарной линейной системы является преобразование Лапласа от весовой (импульсной переходной) функции.

2. 
   С какой целью и каким образом выделяют типовые динамические звенья САУ?
   

Для исследования стационарных линейных систем удобно ввести элементарные типовые стационарные линейные звенья, передаточными функциями которых являются отдельные простейшие множители в формуле:

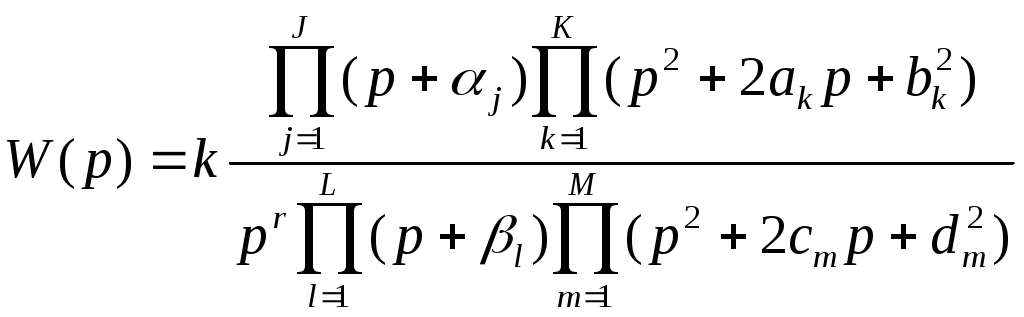; где r – любое целое число

-идеальный дифференциатор

-форсирующее звено 1-го порядка

-форсирующее звено 2-го порядка

-идеальный интегратор

-статическое звено 1-го порядка

-статическое звено 2-го порядка

Этих шести элементарных типовых звеньев достаточно для исследования САУ.

3. 
   Как влияет безынерционное звено на амплитуду и фазу синусоидального входного сигнала?
   

Безынерционное элементарное звено имеет вид: . Таким образом, на выходе сигнал увеличивается в k раз.

4. 
   Какие звенья называются апериодическими?
   

Апериодическое звено – реальное звено, которое можно представить как последовательное соединение статического звена 1-го порядка и интегрирующего идеального звена. Следовательно, апериодическое звено уже не является элементарным типовым звеном.

5. 
   Как проходят через инерционное звено первого порядка гармонические сигналы низкой и высокой частоты?
   

---

Низкие частоты проходят лучше, чем высокие, потому что колебание уменьшается.

6. 
   Какие звенья называются колебательными?
   

звено называют колебательным, так как его временные характеристики носят колебательный характер.

7. 
   При каком соотношении между постоянными времени Т1 и Т2 инерционное звено второго порядка имеет апериодический переходный процесс и при каком – колебательный?
   

При Т₁2Т₂ – апериодический

При Т₁ 2Т₂ – колебательный

8. 
   Какие звенья называются интегрирующими?
   

Звено называется интегрирующим, если ее передаточная функция описывается в интегральной форме.

9. 
   Какие звенья называются дифференцирующими?
   

Звено называется дифференцирующим, если ее передаточная функция описывается дифференциальными уравнениями

10. 
    Чем отличаются идеальные дифференцирующее и интегрирующее звенья от реальных?
    

Реальное звено не пропускает равномерно все частоты от 0 до ∞, а имеет определенную полосу пропускания, в отличии от идеальных.

11. 
    Почему дифференцирующие звенья плохо пропускают медленно меняющиеся входные сигналы?
    

Потому что выходной сигнал пропорционален производной по времени от входного.

---

Смотрите также файлы

• Интерференция наблюдается при сложении таких волн, у которых разность фаз постоянна во времени.docx

• Лекция Литературный язык в системе русского национального языка Учебные вопросы.pdf

• Вопросы первой команде 1 от 1 тысячи тенге. (10 тенге).doc

• Формирование безбарьерной среды.docx

• Методические рекомендации по оказанию социальнобытовых услуг при реализации технологий ухода получателям социальных услуг с.pdf