3-деңгей

95. 
    Дифференциалдық теңдеу ұғымы.
    

Анықтама. Құрамында тәуелсіз айнымалы х, ізделінді y=f(x) функциясы және оның туындылары болатын теңдеу дифференциалдық теңдеу деп аталады. Дифференциалдық теңдеуді шешкенде оның шешіміне С тұрақтысы енеді. Мұндай шешімдер дифференциалдық теңдеудің жалпы шешімі деп аталады. Ол y=ф(х,у) түрінде болады.

Берілген дифференциалдық теңдеуді шешу немесе интегралдау – оның жалпы шешімін табу болады. Дифференциалдық теңдеудің жалпы шешімінен С – тұрақтысының белгілі бір мәніндегі шешімін дифференциалдық теңдеудің дербес шешімі деп аталады.

95. 
    Коши есебі. Коши теоремасы. Бастапқы шарттарды қанағаттандыратын y = f(x ,y ,y ) теңдеуінің дербес шешімін табу Коши есебі деп аталынады. х аргументіне және кез келген С1 мен С2 тұрақтыларына тәуелді у =  ( х, с1, с2 ) функциясы төменднгі екі шартты қанағаттандырса y  = f(x ,y ,y ) теңдеуінің жалпы шешімі деп аталынады. Берiлген 0 x  x болғанда, 0 0 y  y , y   y  болатын бастапқы шарттарды қанағаттандыратын теңдеуiнiң шешiмiн дербес шешiм деп атайды.
    
96. 
    Дифференциалдық теңдеудің геометрялық мағынасы.
    

Айталық, y’=f(x,y) дифференциалдық теңдеуі берілсін және – оның y=ф(х) шешімі болсын. Интегралдық қисықтың кез келген нүктесі арқылы жанама жүргізуге болады. Интегралдық қисыққа әрбір (x,y) нүктесінде жүргізілген жанаманың бұрыштық коэффициенті y’ осы нүктедегі f(x,y) функциясының мәніне тең екені теңдеуден жеңіл байқалады. Демек, y’=f(x,y) теңдігі нүктенің координаттары мен осы нүктеде интегралдық қисықтың графигіне жүргізілген жанаманың бұрыштық коэффициенті y’ арасындағы тәуелділікті орнатады. Интегралдық қисықтың әрбір (x,y) нүктесіне бұрыштық коэффициенті f(x,y) болатын бағытталған кесіндіні сәйкестендірейік, сонда берілген теңдеудің бағыттар өрісін аламыз.

Сонымен, геометриялық тұрғыдан y’=f(x,y) теңдеуі xoy жазықтығындағы бағыттар өрісін анықтайды, ал шешім – интегралдық қисық, оның әрбір нүктесінде жүргізілген жанаманың бағыты өрістің бағытымен беттеседі.

95. 
    Айнымалысы ажыратылатын дифференциалдық теңдеу.
    

f2(y)dy = f1(x)dx түріндегі теңдеу айнымалылары ажыра- тылған, ал dy/dx=f(x)g(y)(1) айнымалылары ажыратылатын (жіктелетін) теңдеу деп атала- ды. Егер g(y)≠0,онда(1)теңдеуді:dy/ g(y) = f(x)dx түріне келтіріп, шешімін табамыз: ∫dy/g(y) −∫f(x)dx=C.Мұнда, g(C0 ) = 0 болса, онда y = C0 функциясы да теңдеудің шешімі екендігін ескеру керек. Осы сияқты,f1(x)φ1(y)dx + f2(x)φ2(y)dy = 0 (2) теңдеуін интегралдағанда, f2 (x) = 0 жəне φ1(y) = 0 интегралдық қисықтары да ескерілуі керек. Егер f2 (x)

---

φ1(y) ≠ 0 болса, онда теңдеудің шешімі:

∫ f1(x)dx/f2(x) + ∫φ2(y)dy/ф1(у) =C

95. 
    Бірінші ретті біртекті дифференциалдық теңдеу. Белгісіз функция жəне оның туындысы бойынша сызықтық, біртекті емес (біртексіз) теңдеу деп аталады. Егер f (x) ≡ 0 болса, теңдеу: ( ) 0 dy pxy dx + = (2) сызықтық біртекті делінеді. Қарастырылып отырған аумақта px f x ( ), ( ) функциялары үздіксіз. Біртекті теңдеудің ( ) 0 dy pxy dx + = шешімі: (), dy pxy dx = − () , dy p x dx y = − ln ( ) ln y p x dx C =− + ∫ ( ) . p x dx y Ce −∫ =
    
96. 
    Біртекті теңдеуге келтірілетін дифференциалдық теңдеулер.
    

Мұндай теңдеулерге 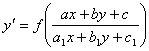түріндегі теңдеулер жатады.

1) Егер анықтауыш 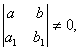 онда

алмастыруын енгіземіз, мұндағы  және  сандары- 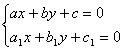жүйесінің шешімдері.

2) Егер алғашқы 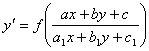 теңдеуде анықтауыш  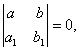онда алмастыруын жасаймыз.

95. 
    Бірінші ретті сызықты теңдеулер. р. Функция мен оның туындысы бойынша сызықты теңдеуді сызықты дифференциалдың теңдеу деп атайды. Әдетте сызықты теңдеуді мына түрде қарастырады. Dy/dx+p(x)y=Q(X)
    

Белгісіз функция жəне оның туындысы бойынша сызықтық, яғни

Dy/dx + p(x)y = f(x) (1) теңдеуі, сызықтық біртекті емес (біртексіз) теңдеу деп атала- ды. Егер f (x) ≡ 0 болса, теңдеу:dy/dx + p(x)y = 0 (2)сызықтық біртекті делінеді.

Қарастырылып отырған аумақта p(x), f (x) функциялары үздіксіз.

Біртекті теңдеудің dy/dx + p(x)y = 0 шешімі: Dy/dx = −p(x)y, dy/y = −p(x)dx, ln y = −∫ p(x)dx + lnC y =Ce^−∫p(x)dx.

95. 
    Бернулли теңдеуі.
    

Y’+P(x)y + Q(x)y^n (10) теңдеуі Бернулли теңдеуі деп аталады. Мұнда n – кез келген заттық сан.

Егер n=0 , я n=1 болса, Бернулли теңдеуі сызықты теңдеуге айналады. Айталық n ≠ 0 ; n ≠1. Онда Бернулли теңдеуін сызықты теңдеуге келтіруге болады. Ол үшін y ≠0 деп алып, (10) теңдеудің екі жағын да y^-n функциясына көбейтеміз:

y^-n• y’ +P(x)y^(1-n)=Q(x). (11)

Енді y^1-n= z, y =z^1/1-n алмастыруын енгіземіз. Онда бұнымен

---

(1- n)y^-n• y’екенін ескеріп, (11) теңдеуді 1 – n санына көбейтсек, z’+ (1-n)P(x)z = (1- n)Q(x) сызықты теңдеуін аламыз. Бұл теңдеудің жалпы шешімін тауып, ондағы z - тің орнына y^1-n қойсақ, Бернулли теңдеуінің жалпы шешімі мына түрде y(x)=e^-SP(x)dx(C+(1+n)SQ(x)e^(1-n)SP(x)dxdx)^1/1-n алынады. Жалпы шешімді табу барысында y ≠ 0 деп есептедік.

103. 
     Риккати теңдеуі. Анықтама:Туындысына қарағанда шешілген және оң жағы ізделінетін функция у-тің квадраттық функциясы болып келген теңдеу, яғни мынадай дифференциалдық теңдеу
     

Риккати теңдеуі деп аталады.

103. 
     Толық дифференциалды теңдеу.
     

.Егер дифференциалданатын қос аргументті u(x, y) функциясы табылып,

М (х, у)dx + N(x, y)dy =0 (1)

теңдеуінің сол жағы осы функцияның толық дифференциалына тепе-тең болса, яғни М(х,у)dx+N(x,y)dy=du(x,y), кезкелген (x,y)ЕD, онда (1) теңдеуді толық дифференциалды теңдеу деп атайды. Мұндағы Д – (1) теңдеудің анықталу облысы. Ол бір байланысты деп есептелінеді және кез келген (x,y)ЕD үшін М2(х,у)+N2(x,y)>0. Толық дифференциалды теңдеуді әрқашан мына түрде du(x, y) = 0жазуға болады. Сондықтан оның жалпыинтегралыбылайжазылады: u(x,y)=С. (2) Мұндағы u(x,y) - теңдеудің интегралы. Толық дифференциалды теңдеудің ерекше шешімі болмайды.

103. 
     Интегралдаушы көбейткіштер.
     

Айталық

M(x,y)dx+N(x,y)dy=0, (x,y)ЕD (11)

диференциалдық теңдеуі толық диференциалды болмасын, яғни dM/dy ≠dN/dx .Бұл жағдайда (11) теңдеуді қолайлы бір функцияға көбейту арқылы толық дифференциалдыға келтіруге болуы мүмкін. Егер ондай функция табылса, оны интегралдық көбейткіш деп атайды.

103. 
     Туынды бойынша шешілмеген теңдеулер.
     

Туындысы бойынша шешілмеген теңдеуді F(x, y, y′) = 0 (1) мүмкін болса y′ арқылы шешіп бір немесе бірнеше 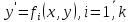(2) теңдеулерді аламыз. Көп жағдайда бұлай шешу мүмкін бола бермегендіктен теңдеу (1) параметр енгізу əдісімен шешіледі. Келесі жағдайларды қарастырайық:

1. Теңдеу (1) мына түрде берілсін F( y′) = 0, (3) жəне бұл теңдеудің кемінде бір нақты түбірі 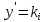болсын. Онда 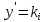, бұдан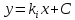

---

немесе , 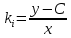, ал 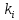теңдеудің (3) түбірі болғандықтан 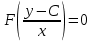интегралын аламыз.

2. Теңдеу (1) мына түрде берілсін: F(x, y′) = 0 (4). Параметр t енгіземіз: 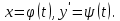Онда 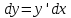теңдігінен 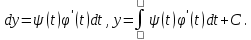∫ Сонымен теңдеудің (4) интегралдық сызықтары параметрлі түрде анықталады: 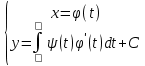. Егер теңдеу (4) х бойынша оңай шешілсе 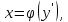онда y′ = t параметрі енгізіледі. Онда: 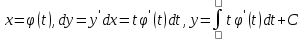интегралдық сызық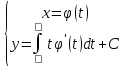

3.Теңдеу (1): F( y, y′) = 0 (5) түрінде берілсе, параметр: 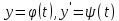болып енгізіледі. Енді 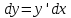теңдігінен 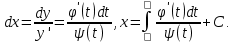Сонымен, интегралдық сызықтар: 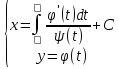түрінде анықталады. Дербес жағдайда теңдеу у бойынша оңай шешілсе 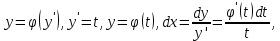шешімді: 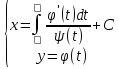түрде табамыз

103. 
     интегралдық қисық.
     

Интегралдық қисық - дифференциалдық теңдеулердің немесе дифференциалдық теңдеулер жүйесінің шешімін бейнелейтін қисық.[1]Алғашқы функциялар тұрақтыға дейін анықталғандықтар әр тұрақтыға сәйкес график сызылып — интегралдық қисық деп аталады.

103. 
     Бірінші ретті -ші дәрежелі теңдеу. . Сол жағы туынды бойынша n - ші дәрежелі көпмүшелік болатын дифференциалдық теңдеуі бірінші ретті n -ші дәрежелі дифференциалдық теңдеу деп аталады
     
104. 
     Толымсыз теңдеулер. Егер F(x, y, y ) 0 теңдеуіндегі F(x, y, y ) функциясы х,у айнымалыларының біреуінен не екеуінен бірдей айқындалмаған түрде тәуелді болмаса онда теңдеуді толымсыз дифференциалдық теңдеу деп атайды
     
105. 
     Клеро теңдеуі.
     

Клеро теңдеуі – y=xy'+f(y') түріндегі 1-ретті жай дифференциалдық теңдеу (мұндағы f – берілген дифференциалданатын функция). Бұл теңдеуді тұңғыш рет француз математигі әрі астрономы А.Клеро (1713 – 1765) қарастырған (1734). Клеро теңдеуі шекті түрде интегралданады. Клеро теңдеуінің жалпы шешімі: y=Cx+f(С) (*) түріндегі түзулер үйірі, мұндағы

---

С – кез келген тұрақты. Клеро теңдеуінің мұндай жалпы шешімінен басқа: x=–f '(p), y=–pf(p)+f Лагранж теңдеуінің дербес жағдайы Клеро теңдеуі деп аталады

111. Лагранж теңдеуі. Лагранж теңдеуі деп х пен у айнымалылары бойынша сызықты y  x (y ) (y ) таңдеуін атайды. Мұндағы  ,  функциялары үзіліссіз деп есептелінеді және (y )  y  . Лагранж теңдеуін Клеро теңдеуін интегралддау сияқты көмекші параметр енгізу арқылы орындалады. y   p десек (14) теңдеу y  x (p) (p) түрінде жазылады.

112. 
     Қисықтар үйірінің июшісі (орағытпасы). Егер L сызығының әрбір нүктесіне қисық сызық үйірінің белгілі бір қисығы жанасатын болса, онда L сызығын бір параметрлік сызықтар үйірінің июшісі (орағытпасы) деп атайды Мысал үшін 2 2 2 (xС)  y  R сызықтар әулетін қарастырайық. Мұндағы R-тұрақты, С –параметр. Бұл сызық центрі Ох өсінің бойында жататын, ал радиусы R болатын шеңберлер үйірі. у = R және у = -R түзулері шеңберлер үйірінің орағыттасы болып табылады.
     
113. 
     Бірінші ретті дифференциалды теңдеудің ерекше шешімдері. орағытпа өзінің әрбір нүктесінде қисықтар үйірінің белгілі бір сызығымен жанасады. Демек, әрбір ортақ нүктеде орағытпа мен қисықтар үйірінің қисығы бірдей x, y, y  мәндерін қабылдайды. Сондықтан орағытпада дифференциалдық теңдеудің интегралдық қисығы болады. Бірақ орағытпа қисықтар әулетінің сызығы болмайды, яғни теңдеудің жалпы шешімінен алынбайды. Парамет С-ның кез келген мәнінде дифференциалдық теңдеудің жалпы шешімінен алынбайтын теңдеудің шешімін ерекше шешім деп атайды.
     

114. Траектория туралы есеп. Айталық (х,у) жазықтығында бір параметрлі қисық сызықтар үйірі (тобы) (x, y,С) 0 (1) берілсін. (x, y,С) 0 үйірдің барлық қисықтарын тек бір ғана тұрақты  бұрышымен қиятын қисықты осы үйірдің изогоналдық траекториясы деп атайды. Егер   /2 болса, изогоналдық траектория ортогоналдық траектория деп аталынады.

115. 
     Екінші ретті дифференциалдық теңдеу. Екінші ретті дифференциалдық теңдеу деп тәуелсіз айнымалы х, ізделінді функция у пен оның бірінші у және екінші у  туындыларын байланыстыратын теңдеуді атайды. Дербес жағдайда екінші ретті дифференциалдық теңдеулерде х, у, y - лер теңдеудің құрамында болмауы да мүмкін, бірақ ізделінді функциядан екінші ретті туынды міндетті түрде болады. Екінші ретті дифференциалдық теңдеудің жалпы түрі мынадай болады: Fx, y, y  , y  0 Егер теңдеу екінші ретті туындыға қатысты шешілетін болса, онда ол былай жазылады: y  = f (x ,y ,y ). Екiншi реттi дифференциалдық теңдеулердiң жалпы шешiмi y(x,C1,C2) түрiнде берiлiп, оның өрнегiне екi тұрақты C1 C2 , сандары кiредi.
     
116. 
     Екінші ретті дифференциалдық теңдеудің ретін төмендету. Екінші ретті дифференциалдық түрлендірулерден, кейбір теңдеулерден кейін бірінші ретті теңдеулермен алмастыруға болатындары болады. Екінші ретті дифференциалдық теңдеулерді осындай түрлендіру олардың ретін төмендету деп аталады.
     
117. 
     y² = f(x) түріндегі теңдеу. Бұл теңдеудің құрамында у жоқ, онда мұндай теңдеуді z(x)=y' жаңа белгісіз функциясын енгізу арқылы ретін төмендетуге болады.Сонда y''=dz/dx болып теңдеу dz/dx=f(x,z) түріне келеді.Бұл соңғы теңдеуді бұрын өтілген, бірінші ретті дифференциалдық теңдеулерді шешу әдістерінің бірін қолданып интегралдасақ, теңдеудің z=q(x,C1) түріндегі жалпы шешімі шығады.Бірақ z = y' болғандықтан, белгісіз функция у-ті табу үшін,у'=q(x,C1) теңдеуінің жалпы шешімін табу керек,яғни бірінші ретті тағы бір дифференциалдың теңдеуді интегралдарға тура келеді
     
118. 
     Құрамында у жоқ екінші ретті теңдеу.
     

---

Смотрите также файлы

• Реферат на тему Нарушение строения и функции артикуляционного аппарата при ринолалии.docx

• Срсен Аманжолов атындаы Шыыс азастан Университеті.docx

• Отчет по лабораторной работе 1 на тему Исследование устойчивости системы с использованием критерия Гурвица.docx

• Продолжение таблицы 1 на плане.docx

• 2 Расчётноконструкторская часть.docx