Екінші ретті дифференциалдық теңдеу деп тәуелсіз айнымалы х, ізделінді функция у пен оның бірінші у және екінші у  туындыларын байланыстыратын теңдеуді атайды. Дербес жағдайда екінші ретті дифференциалдық теңдеулерде х, у, y - лер теңдеудің құрамында болмауы да мүмкін, бірақ ізделінді функциядан екінші ретті туынды міндетті түрде болады.

Егер теңдеу екінші ретті туындыға қатысты шешілетін болса, онда ол былай жазылады: y = f (x ,y ,y ).

Осы теңдеудіңөрнегiнде y жоқ, яғни y   f ( y ) Бұл теңдеудi Z  y  ауыстыру енгiзу арқылы шешемiз. Сонда Z  y  , Z  f (Z) аламыз. Бұл бiрiншi реттi теңдеу.

115. 
     Құрамында х айнымалысы жоқ екінші ретті теңдеу.
     

Екінші ретті дифференциалдық теңдеу деп тәуелсіз айнымалы х, ізделінді функция у пен оның бірінші у және екінші у  туындыларын байланыстыратын теңдеуді атайды. Дербес жағдайда екінші ретті дифференциалдық теңдеулерде х, у, y - лер теңдеудің құрамында болмауы да мүмкін, бірақ ізделінді функциядан екінші ретті туынды міндетті түрде болады.

Егер теңдеу екінші ретті туындыға қатысты шешілетін болса, онда ол былай жазылады: y = f (x ,y ,y ).

Осы теңдеудің өрнегiнде тәуелсiз айнымалы x жоқ, яғни y   f ( y). Бұл теңдеудi интегралдау x - тiң орнына жаңа тәуелсiз айнымалылы y - тi енгiзу арқылы жүзеге асырылады y   Z( y).Сонда 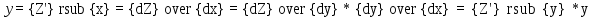. Сөйтiп y   Z,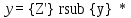

115. 
     У және оның туындыларына қатысты біртекті екінші ретті теңдеу.
     

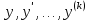-ке байланысты біртекті екінші ретті теңдеу: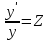

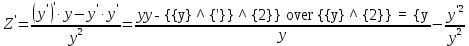
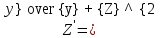
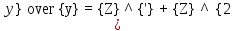
115. 
     Тұрақты коэффициенттi екiншi реттi сызықтық дифференциалдық теңдеулер.
     

Тұрақты коэффициенттi екiншi реттi сызықтық дифференциал-дық теңдеулер деп мына түрде берiлген теңдеулердi айтамыз: 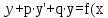(1). Мұнда p,q тұрақты сандар.

115. 
     Тұрақты коэффициенттi екiншi реттi сызықтық біртекті дифференциалдық теңдеулер.
     

Тұрақты коэффициенттi екiншi реттi сызықтық дифференциал-дық теңдеулер деп мына түрде берiлген теңдеулердi айтамыз:

---

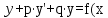(1). Мұнда p,q тұрақты сандар.

Егер f (x)  0 болса, онда бұл теңдеу бiртектi теңдеу деп аталады 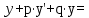, (2) 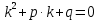(3) теңдеуi (2) теңдеуiнiң характеристикалық теңдеуi деп аталады. (2) теңдеуiнiң жалпы шешiмi (3) характеристикалық теңдеуiнiң түбiрлерiне байланысты анықталады:

1. Егер 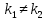болса, онда .

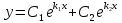2. Егер 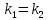болса, онда .

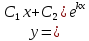3. Егер 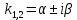болса, онда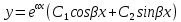

115. 
     Тұрақты коэффициенттi екiншi реттi сызықтық біртексіз дифференциалдық теңдеулер.
     

Тұрақты коэффициенттi екiншi реттi сызықтық біртексіз дифференциалдық теңдеулер. :Тұрақты коэффициенттi екiншi реттi сызықтық дифференциалдық теңдеулер деп мына түрде берiлген теңдеулердi айтамыз: y"+p•y'+q•y=f(x) Мұнда p,q тұрақты сандар. Егер теңдеуде f(x) тең емес нольге болса , онда теңдеу біртексіз теңдеу деп аталады. Бiртекті емес теңдеудiң жалпы шешiмi екi шешiмнiң қосындысынан тұрады:

y=y*+y'

115. 
     Оң жағы арнайы түрде берілген коэффициенттері тұрақты біртекті емес сызықты дифференциалдық теңдеулердің дербес шешімін табу. бастапқы шарттары үшін 0 0 2 0 1 , ,..., n с с с мәндері табылып, ( , , ,..., ) 0 0 2 0 1 n y  y x с с с шешімі берілген бастапқы шарттарды қанағаттандырса, онда (4) функцияны (3)-ші теңдеудің жалпы шешімі деп атайды. Егер жалпы шешімі айқындалмаған функция ( , , , ,..., ) 0 1 2   n x y с с с түрінде берілсе, оны теңдеудің жалпы интегралы деп атайды. (4) жалпы шешімнен n с ,с ,...,с 1 2 тұрақтыларының белгілі бір сандық мәндерінде алынатын кез келген шешімді теңдеудің дербес шешімі дейді.
     

125. 
     Эйлердің дифференциал теңдеуі.
     

Коэффициенттері a_i тұрақтылар, a_0 x^n y^((n))+a_1 x^(n-1) y^((n-1))+⋯+a_(n-1) xy^'+a_n y=0, түрдегі теңдеулер Эйлер теңдеулері деп аталадыб айнымалы x=-e^t (немесе x=-e^t, егер x<0) алмастыруымен, тұрақты коэффициентті біртекті теңдеуге келтіріледі.

125. 
     Дифференциалдық теңдеулер жүйесі. Бір теңдеуге келтіру тәсілі. Коэффициенттері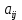 немесе матрицасы A тұрақты сызықты теңдеулер жүйесін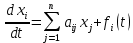 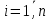немесе векторлық түрде 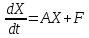, тұрақты коэффициентті сызықты теңдеулер жүйесі деп атайды. Тұрақты коэффициентті сызықты теңдеулер жүйесі жоғарғы ретті сызықтық бір теңдеуге келтіріліп, интегралданады.
     

---

Теңдеулер жүйесінің 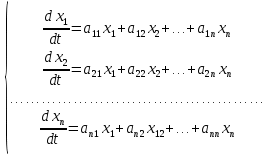(1) шешімдерін ,

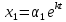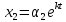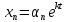,...., түрінде іздестіреміз.

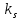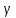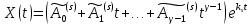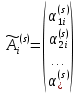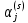Теңдеулер жүйесі (1) жоғарғы ретті сызықты бір теңдеуге кел тірілетіндігін ескерсек, сипаттамалық түбірінің еселігі болғанда, бұл түбірге тиісті шешімі мына түрде іздестіріледі , (2) , -тұрақтылар. Шешімді (2) жүйеге (1) қойып, матрицаларды 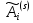анықтайды.

125. 
     Тұрақты коэффициентті сызықты дифференциалдық теңдеулержүйесі Эйлер тәсілі. қ біртекті теңдеулер жүйесі берілсін Мұндағы , , i 1,2,3 i c i b i a - тұрақтылар. Бұл теңдеуді үшініші ретті біртекті теңдеуге келтіруге болады және алынатын теңду-коэффициенттері тұрақты теңдеу болады.
     

---

Смотрите также файлы

• Реферат на тему Нарушение строения и функции артикуляционного аппарата при ринолалии.docx

• Срсен Аманжолов атындаы Шыыс азастан Университеті.docx

• Отчет по лабораторной работе 1 на тему Исследование устойчивости системы с использованием критерия Гурвица.docx

• Продолжение таблицы 1 на плане.docx

• 2 Расчётноконструкторская часть.docx