ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание №1
| Вариант | Рис. | Е,В | L,Гн | С, Ф | R1 | R2 | R3 | R4 | Определить |
| Ом | |||||||||
| 60 | 4-14 | 50 | 10-3 | 10-4 | 4 | 6 | 10 | 10 | i2 |
-
Классический метод
L iL R2
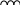












 R1 i3
R1 i3 





 C i2 R3 R4
C i2 R3 R4


E

Определим ток через индуктивность L и напряжение на ёмкости C в момент времени t=0_
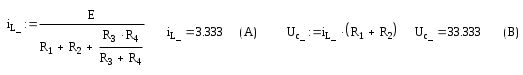
Определяем принуждённые составляющие тока через индуктивность, напряжения на емкости:
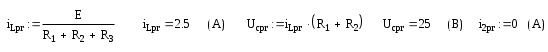
Отсюда можно найти свободные составляющие тока через индуктивность и напряжения на ёмкости в момент времени t=0,учитывая первый закон коммутации
Составим характеристическое уравнение для приведённой схемы, разорвав ёе предварительно в месте ЭДС.
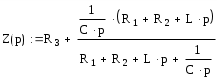
Приравнивая Z(p)=0 решаем получившееся уравнение относительно p:
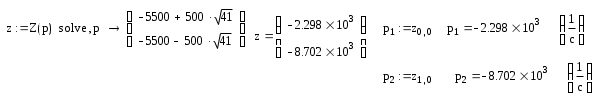
При двух корнях характеристического уравнения решение для свободной составляющей имеет вид:
i2ccb(t)=A1*ep1t+ A2*ep2t
А для момента времени iccb0 и её производная имеют вид:
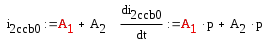
Найдём неизвестные коэффициенты, применяя законы Кирхгофа к рассматриваемой схеме (в момент времени t=0), а также их производные первого порядка (так как степень характеристического уравнения равна 2).
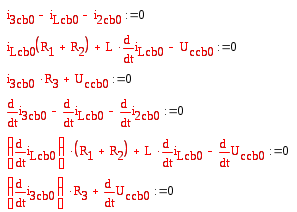
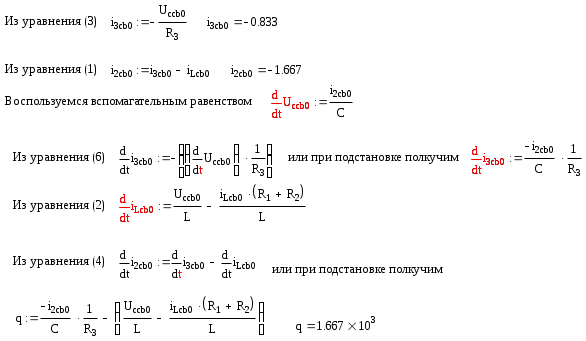
При известном dUccb0/dt=0, система уравнения относительно неизвестных коэффициентов становится разрешимой
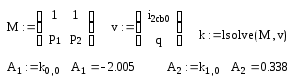 . Тогда:
. Тогда: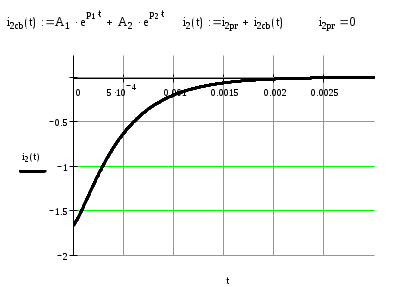
-
Операторный метод
Составим схему замещения для выше приведённой электрической схемы.
Lp I1(p) R2 LiL_



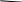







 R1 I3(p)
R1 I3(p)  1/Cp
1/Cp 





 I2(p) R3
I2(p) R3 
U
 c_/p_
c_/p_ E/p
E/p 
Аналогично выполняем расчёт для
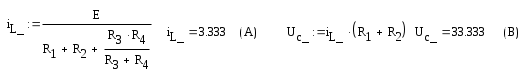
Рассчитаем токи действующие в ветвях схемы по МКТ.
Составляем систему уравнений:
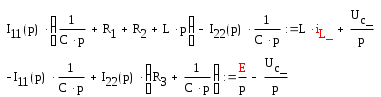
Решаем систему методом Крамара -Копели
Составляем определитель коэффициентов и раскрывая его, упрощаем:
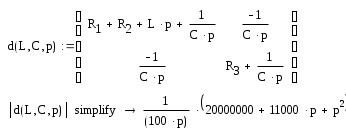
Затем:
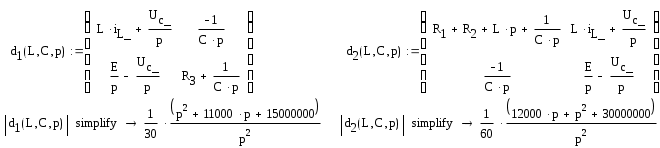
Тогда контурные токи будут определены в виде
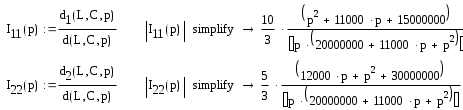
А отсюда
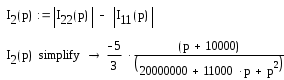
Найдём корни характеристического уравнения
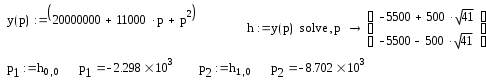
Делаем необходимые преобразования над получившимся изображением I2(p) получаем закон изменения тока при переходном процессе.
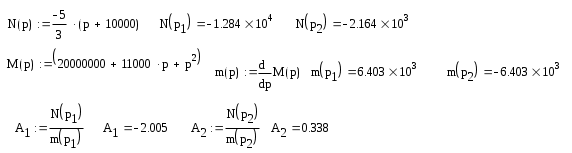
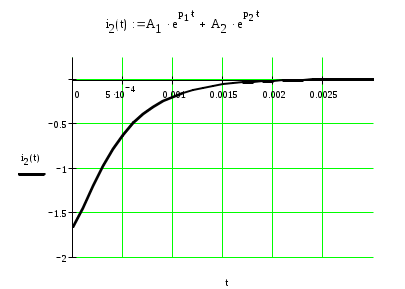
Задание №2
Требуется определить закон изменения во времени тока i3(t) во второй ветви, схемы приведённой ниже, интегралом Дюамеля.
I1(p)






 I3(p) I3(p)
I3(p) I3(p) 


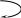 R 2R
R 2R 

 1/p II 1/Cp
1/p II 1/Cp 


 I
I III
III 
 2R R
2R R

Где входное напряжение имеет сложную форму вида:
U1



U1=-А/2+k*t
А


A/2 0 t1 t

Определим переходную проводимость g(t) для исследуемой схемы, для этого подадим на вход схемы U=1 (B), то i3(t)=U*g(t) примет вид i3(t)=g(t), где g(t)- переходная проводимость .Расчёт ведётся при нулевых начальных условиях, поэтому UC(-0)=0.
Рассчитываем ток I3(p) методом контурных токов:
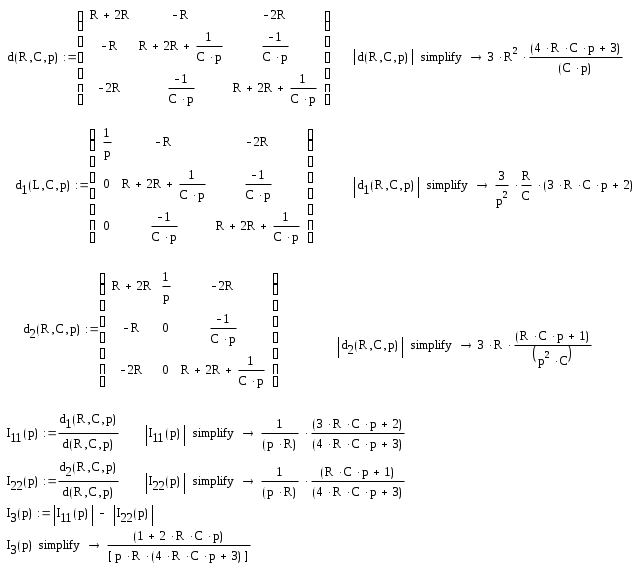
Преобразуем получившееся изображение I3(p) в функцию от времени, т.е. в i3(t).
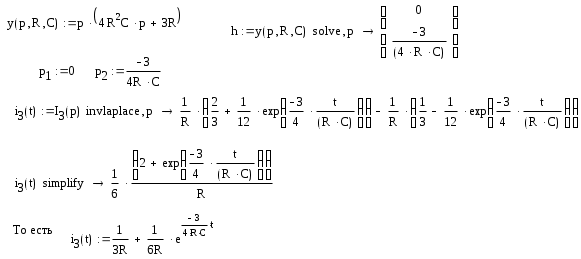
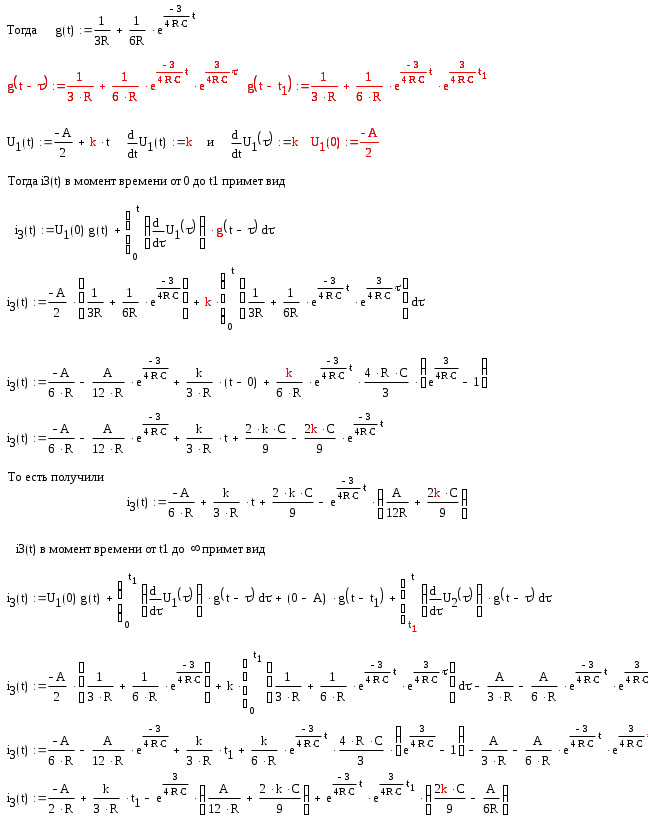
Задание №3
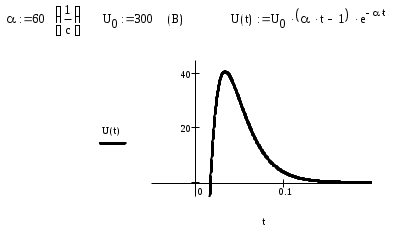
Задан спектр некоторой функции U(t)=U0(αt - 1)e-αt , где α=60 1/с, U0=300 B. U(t) задана на графике:
3.1 Получим аналитическое выражение для модуля и аргумента спектра функции U(t).
Используя табличные значения преобразуем оригинал функции U(t) в её изображение.
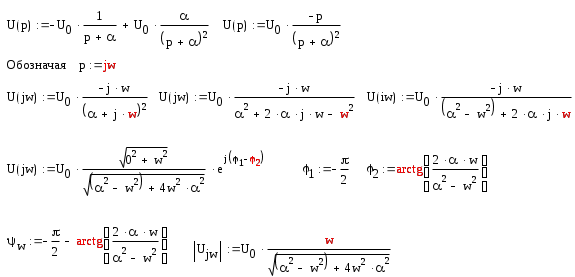
3.2 Представление выражения |Ujw| в виде функции от w/α
Преобразуем выражение
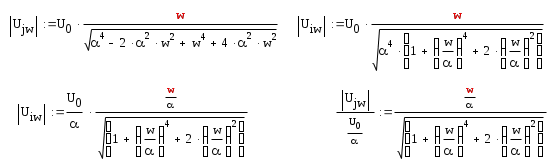
3.3 Построение найденной функции