«Теория случайных процессов».

Лектор: Борисов Андрей Владимирович, проф. каф. 804

Borisych@me.com

Рекомендуемая литература:

1. 
   Миллер Б.М., Панков А.Р. Теория случайных процессов в примерах и задачах. М.: Физматлит, 2002. - 320 с.
   
2. 
   Ширяев А.Н. Вероятность. М.: Наука, 1989.
   
3. 
   Боровков А.А. Теория вероятностей. М.: URSS, 2009.
   
4. 
   Булинский А.В., Ширяев А.Н. Теория случайных процессов. М.: Физматлит, 2005.
   

Лекция 13. Предэкзаменационная консультация.

1. 
   Общие сведения и советы
   
2. 
   Решение избранных задач
   

Общие сведения и советы

1. 
   В билете 4 задачи. Рациональное решение каждой составляет не более полстраницы рукописного текста.
   
2. 
   Все задачи новые. Искать решение в Интернете бессмысленно.
   
3. 
   Все задачи базируются на теоретических сведениях, представленных в лекциях.
   

Решение избранных задач
Задача 1. Пусть 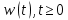– стандартный винеровский процесс, 0 < t₁ < t₂ – некоторые фиксированные моменты времени. Найти плотность распределения случайной величины X = min(w( 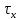+t₁), w( 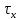+t₂)), где – момент первого пересечения процессом 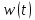положительного порога x.
Решение:

Из определения момента 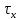следует, что w( 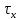)=x, а из свойств винеровского процесса следует, что w( 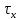+t) = x+v(t), где v(t) – также стандартный винеровский случайный процесс. Отсюда следует, что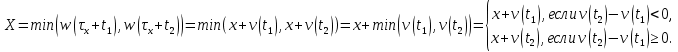



Вновь из свойств винеровского процесса следует, что 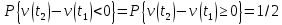, а также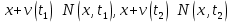

---

. Поэтому по формуле полной вероятности искомая плотность распределения X является двухкомпонентной «смесью» упомянутых выше гауссовских плотностей:


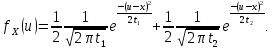
Задача 2. Пусть 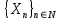- последовательность центрированных случайных величин: 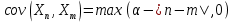, где 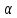– известное неслучайное натуральное число. Имеет ли последовательность СК-предел? Ответ обосновать.
Решение:
Согласно лемме Лоэва 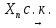тогда и только тогда, когда существует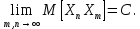



Рассмотрим два частных предела 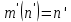и 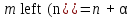Легко видеть, что

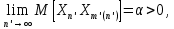в то время как 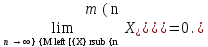Таким образом, имеются два частных предела, которые не совпадают. Значит, 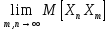не существует, т.е. 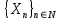не сходится в СК-смысле.
Задача 3. Пусть 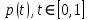– стандартный пуассоновский процесс, q(t) = p(t) – tp(1) – пуассоновский мост. Является ли он сильно непрерывным на ?
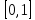Решение:

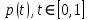– стандартный пуассоновский процесс, имеющий кусочно-постоянные траектории. Поэтому 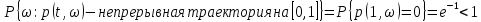, поэтому q(t) не является сильно непрерывным на .
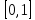Задача 4. Пусть

---

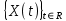
- стационарный случайный процесс. Будет ли стационарным процесс Y(t) =1/(2h)( X(t+h)-X(t-h)), где h – известное неслучайное число. Ответ обосновать. В случае, если Y(t) будет стационарным найти частотную характеристику соответствующего преобразования и дисперсию.
Решение:

Одним из способов ответить на первый вопрос является непосредственная проверка условий M[X(t)] = Const, и cov(X(t),X(s))=k(t-s). Однако, в данном случае экономичнее попытаться вычислить частотную характеристику.



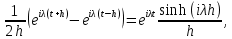
откуда следует, что функция 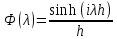не зависит от t, т.е. действительно является частотной характеристикой. Если функция будет зависеть от t, то Y(t) – результат стационарного преобразования стационарной случайной функции. Он также будет стационарной случайной функцией, если Y(t) будет иметь конечную дисперсию. Найдем ее: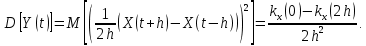


Задача 5. В начальный момент времени имеется N частиц. Рассматривается дискретное время. За один шаг по времени каждая частица, независимо от остальных может распасться с вероятностью p. Доказать, что число X_t частиц, не распавшихся до момента времени t образуют марковскую цепь. Найти матрицу переходных вероятностей цепи на t-м шаге.

Решение:
Возьмем произвольный натуральный момент времени t и невозрастающий набор натуральных значений



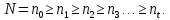
Тогда по условию задачи (независимое поведение отдельных частиц, геометрическое распределение времени жизни) получаем



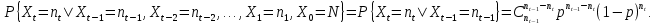
Это и есть элементы матрицы переходных вероятностей:


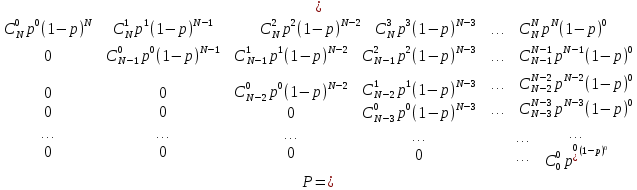
В данной матрице P_ij = P{X_t=N-j+1|X_t=N-i+1}.

---

Смотрите также файлы

• Практикум 1 1 По объявлениям о продажи квартир составьте базу исходной информации в виде.docx

• Отчет по лабораторной работе должен содержать 1 Тему работы 2 Цель работы 3 Ход работы 4 Постановки задач.docx

• Тема Времена года. Прошлым летом Jahreszeiten. Im Sommer.docx

• Программа среднего профессионального образования 38. 02. 01. Экономика и бухгалтерский учет (по отраслям) соо дисциплина Естествознание Практическое задание 1.docx

• .docx