МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ

КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное

бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»



Кафедра «Информатика»

Лабораторная работа № 1

по теме

«Методы решения нелинейных уравнений»

по дисциплине «Численные методы»

Выполнил:

Проверил:

Москва

1. Задание

1. 
   Выбрать индивидуальное задание из табл. 1-1:
   

• 
  нелинейное уравнение;
  
• 
  методы решения нелинейного уравнения для выполнения 3-х итераций;
  

2. 
   Отделить корни заданного уравнения графическим и аналитическим методом с использованием средств пакета Scilab.
   
3. 
   Для каждого из заданных методов провести исследование функции нелинейного уравнения:
   

• 
  проверить выполнение условий сходимости вычислительного процесса, в случае расходящегося процесса – сделать необходимые преобразования для обеспечения сходимости;
  
• 
  выбрать начальное приближение к корню;
  
• 
  сформулировать условие окончания этапа уточнения корня.
  

4. 
   С использованием итерационной формуле 1-го заданного методу провести расчет трех итераций с использованием средств мат. пакета. Результаты расчета свести в табл. 1-2.
   
5. 
   Оценить погрешность результата после 3-х итераций.
   
6. 
   Для 2-го заданного метода выполнить решение уравнения с точностью
   

10^-4, создав программу, реализующую заданный метод. Произвести расчет, а результаты решений свести в табл. 1-2.

7. 
   Найти решение нелинейного уравнения на отдел
   

2. Вариант задания

---

4 – метод хорд, а 1 – метод половинного деления.

3. Выполнение

3.1 Этап отделения корня



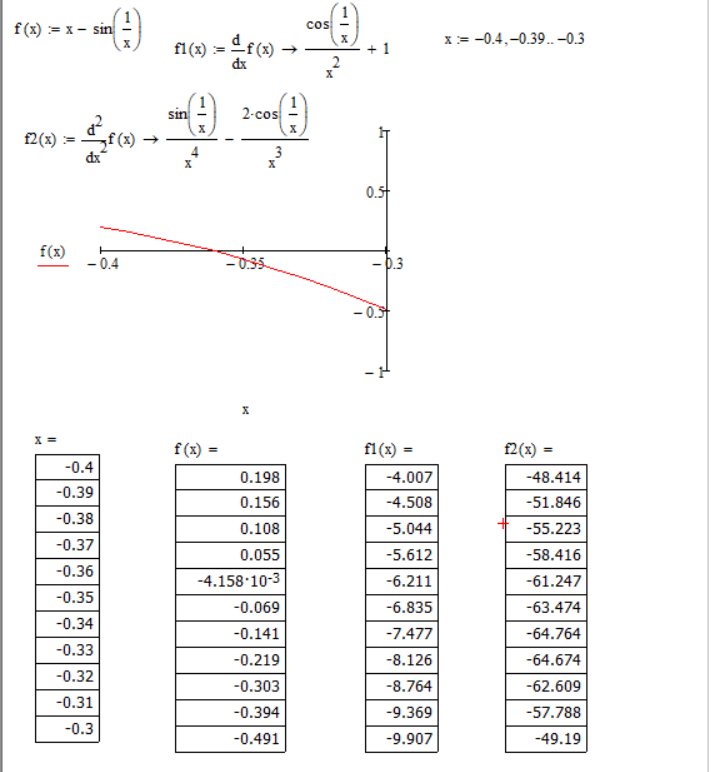
Из построенного графика функции f(x) видно, что на отрезке [-0.4;-0.3] есть один корень. На этом графический способ отделения корней заканчивается.

Другой вариант отделения корня – решить задачу аналитически.

Для аналитического отделения корня построена таблица. Она требует пояснений. В столбцах таблицы выведены некоторые значения аргумента x на заданном отрезке, а также значения функций f(x), 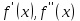при этих значениях x.

Видно, что на отрезке [-0.4;-0.3] функция f(x) меняет знак, значит существует, по крайней мере, один корень.

Значения первой производной 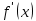в заданных точках отрезка [-0.4;-0.3] не меняет знак, что вызывает некоторую надежду о том, что 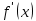не меняет знак на всем отрезке [-0.4;-0.3], но делать вывод об этом не совсем корректно с точки зрения математики. Однако анализ аналитического выражения 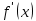= (cos(1/x)/x² ) + 1 приводит к выводу, что 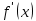< -4 при любых значениях x. А это значит, что 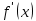отрицательно на всем отрезке [-0.4;-0.3], и уже из этого следует, что на отрезке [-0.4;-0.3] функция f(x) монотонна и имеет один корень.

3.2 Этап уточнения корня

Необходимые и достаточные условия для метода хорд:

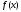непрерывна на [a;b] и 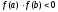, это выполняется

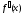и отличны от нуля и сохраняют знаки для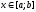

---

, это выполняется

В нашем случае на отрезке [-0.4;-0.3] требования сходимости выполняются.

На этапе отделения корня было показано, что для функции f(x)=x-sin(1/x) вторая производная 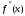<0 на отрезке [-0.4;-0.3] и, следовательно, неподвижной точкой является точка 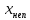= b = -0.3, так как f”(-0.3)*f(-0.3) > 0

Таким образом, полагая 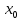= a= -0.4, получим сходящуюся последовательность приближений к корню.

В рассматриваемой задаче рекуррентная формула принимает следующий вид

= +

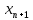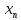Оценку погрешности можно проводить по любой из формул или 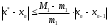, где m1 и M1 – наименьшее и наибольшее значения 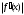на отрезке. В случае, если M1
Для получения решения уравнения методом хорд воспользуемся следующей рекуррентной формулой:



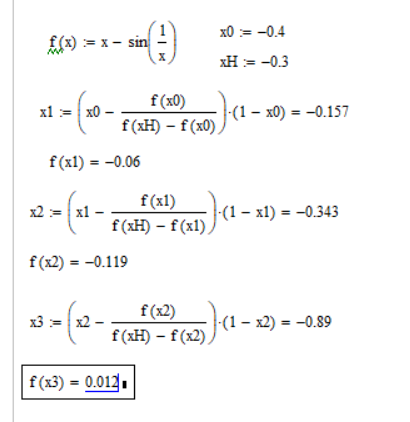
Результаты вычислений представлены в виде следующей таблицы:

n	Xn	f(xn)
0	-0.4	0.198
1	-0.157	-0.06
2	-0.343	-0.119
3	-0.89	0.012

Оценку погрешности результата, вычисленного методом хорд, получим по формуле

---

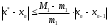
. Тогда после трех итераций

| - | <=

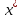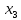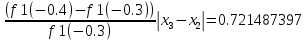
Метод половинного деления, написанный на питоне:

import math
def half_interval(a, b):

    return (a + b) / 2
def get_parametr():

    a = float(input("Введите точку a :"))

    b = float(input("Введите точку b :"))

    E = float(input("Введите точность E:"))
    print('a = {a} Тип:{a1}\nb = {b} Тип {b1}\nE = {E} Тип:{E1}'

      .format(a=a, a1=type(a), b=b, b1=type(b), E=E, E1=type(E))

      )

    return a, b, E

def func(x):

    return x - math.sin(1/x)

def start():

    a, b, E = get_parametr()

    counter = 0

    max_counter = 200

    while abs(b - a) > E:
        counter += 1

        if counter >= max_counter:

            break
        if abs(b - a) <= E:

            break
        print('\n\nШаг №{counter}'.format(counter=counter))

      

        fa = func(a)

        c = half_interval(a, b)

        fc = func(c)

        if fa * fc > 0:

            a = c

        else:

            b = c

        print('fa = {f_a} fc = {f_c} fa * fc = {res}'.format(f_a=fa, f_c=fc, res=fa * fc))

        print('a = {a} b = {b} x = {x} fx = {f_x}'.format(a=a, b=b, x=(a+b)/2, f_x=fc))

к	x	f(x)	a	b
1	-0.375	-0.06937060048564314	-0.4	-0.35
2	-0.3625	0.08227262663581197	-0.375	-0.35
3	-0.35624999999999996	0.011178785065124874	-0.3625	-0.35
4	-0.359375	-0.02788213054197286	-0.3625	-0.35624999999999996
5	-0.3609375	-0.008051858933839195	-0.3625	-0.359375
6	-0.36015625	0.0016379281287689507	-0.3609375	-0.359375
7	-0.36054687500000004	-0.0031882866854368586	-0.3609375	-0.36015625
8	-0.36074218750000003	-0.0007705173213234939	-0.3609375	-0.36054687500000004
9	-0.36064453125000007	0.0004348699202055828	-0.36074218750000003	-0.36054687500000004
10	-0.360693359375	-0.00016753244951156487	-0.36074218750000003	-0.36064453125000007

---

0>

---

Смотрите также файлы

• 2. Бюджетная, налоговая, социальная политика.docx

• Большой Арктический заповедник.docx

• Изучение юридического дискурса в плане интерпретации юридических терминов имеет большое значение в настоящее время, поскольку понятийный объем некоторых лексических единиц структурируется неадекватным способом.docx

• бекітемін келісемін Б отырысында аралды.docx

• В истории человечества можно найти немало случаев геноцида, начиная с древнейших времён и вплоть до наших дней.docx