Файл: Лабораторная работа 1 Проверка основного закона динамики вращательного движения на основе маятника Обербека.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.03.2024
Просмотров: 37
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
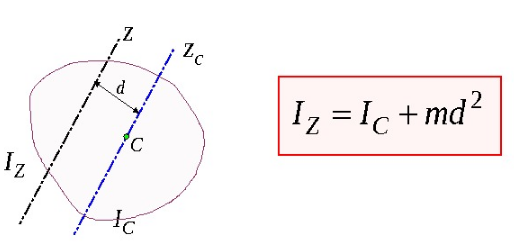
I=Iс+md2
Мнат-Момент силы натяжения нити , Мтр=Момент силы трения, -Угловое ускорение.
Задачи:
3.1. Найти угловую ω и линейную скорости n вращения земной поверхности на экваторе.
Дано: Rз=6,4*106м
Найти: ω - ?
v - ?
Решение: v=l/t -> v= 2пR/86400с -> v=2*3,14*(6,4*106)/86400с ->
-> v= 40212385/ 86400c=465,4м/с
ω=V/R -> ω= 465,4/6,4*106м=72,7*10-6рад/с
Ответ: ω = 72,7*10-6рад/с
v=465,4м/с
3.2. Мотоциклист едет по горизонтальной дороге со скоростью 74 км/ч, делая поворот радиусом кривизны 100 м. На какой угол (Считая от горизонтальной поверхности) при этом он должен наклониться, чтобы не упасть на повороте?
Дано:
V=74км/ч
R=100м
Решение:
1)ац.с=V2/R
2)ox: m*aц.с=N*cosα
oy: o
=N*sinα-mg
N=mg/sinα
Maц.с=mgctgα
ац.с=gctgα
3) V2/R=gctgα
ctgα=V2/Rg=(20,5^2/100*9,81)=0,428
=arcctg(0,428)=66,83°
Ответ:Угол =66,83°

-
Момент вращающей силы, приложенной к телу, равен произведению момента инерции тела на угловое ускорение. M=B*I. -
В данной работе определить момент инерции маятника без грузов можно по формуле I0=Мнат-Мтр/
Мнат-Момент силы натяжения нити , Мтр=Момент силы трения, -Угловое ускорение.
-
В данной работе можно определить массу грузов на стержнях маятника Обербека с помощью формул
M=I*B ; m=p*V ; I=mR2 : R-Расстояния на которых находятся грузы от самой оси вращения; I-Момент инерции с грузами. -
Момент инерции маятника Обербека можно изменить при прикреплении грузов, при изменении высоты падения подвеса, при замене расстояния грузов от оси вращения. -
Насчёт момента инерции маятника-он не изменяется, т.к на него высота никак не зависит. Время опускания подвеса изменится, потому что путь, который будет проходить груз, будет больше. Кинетическая энергия не изменится, по причине того, что она является совокупностью вращательного движения крестовины и поступательного движения подвеса. Угловое ускорение изменится, станет больше, потому что оно зависит от времени.
Задачи:
3.1. Найти угловую ω и линейную скорости n вращения земной поверхности на экваторе.
Дано: Rз=6,4*106м
Найти: ω - ?
v - ?
Решение: v=l/t -> v= 2пR/86400с -> v=2*3,14*(6,4*106)/86400с ->
-> v= 40212385/ 86400c=465,4м/с
ω=V/R -> ω= 465,4/6,4*106м=72,7*10-6рад/с
Ответ: ω = 72,7*10-6рад/с
v=465,4м/с
3.2. Мотоциклист едет по горизонтальной дороге со скоростью 74 км/ч, делая поворот радиусом кривизны 100 м. На какой угол (Считая от горизонтальной поверхности) при этом он должен наклониться, чтобы не упасть на повороте?
Дано:
V=74км/ч
R=100м
Решение:
1)ац.с=V2/R
2)ox: m*aц.с=N*cosα
oy: o
=N*sinα-mg
N=mg/sinα
Maц.с=mgctgα
ац.с=gctgα
3) V2/R=gctgα
ctgα=V2/Rg=(20,5^2/100*9,81)=0,428
=arcctg(0,428)=66,83°
Ответ:Угол =66,83°
