ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.03.2024
Просмотров: 24
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1. Случайные величины.
Определение. Случайной величинойназывается величина, которая в результате опыта может принимать то или иное значение, причем заранее известно какое именно.
Можно дать ещё одно определение случайной величины: случайной величиной называется величина, принимающая в результате испытания одно и только одно числовое значение, зависящее от случайных факторов, которые заранее не могут быть учтены.
Примеры случайных величин:
-
число студентов на занятии; -
количество детей родившихся за сутки; -
время ожидания автобуса на остановке; -
рост любого встреченного на улице человека.
Случайные величины могут быть двух видов: дискретные и непрерывные.
2. Дискретные случайные величины.
Определение. Дискретной случайной величиной называется такая величина, которая в результате опыта может принимать определенные значения с определенной вероятностью, образующие счетное множество (множество, элементы которого могут быть занумерованы).
Это множество может быть как конечным, так и бесконечным.
Например, количество выстрелов до первого попадания в цель является дискретной случайной величиной.
Случайная дискретная величина Х считается заданной, если указано множество значений, которые она может принимать и вероятности появления каждого из этих значений. Эти соотношения между возможными значениями х i и вероятностями их появления pi называются законом распределения случайной дискретной величины.
Приведем примеры на дискретные случайные величины.
Пример 1.Идёт охота на дикого зверя с помощью ловушки. Вероятность попасть в ловушку для волка – 0.3, для медведя – 0.5, для лисы и зайца – 0.6. Найти закон распределения случайной величины Х - числа попавших в ловушку зверей.
Решение. Случайная величина Х может принимать следующие значения: 0, 1, 2, 3 (в ловушку попал один зверь, два, три, ни одного). Рассчитаем вероятности по теоремам алгебры событий:
р1=0,3; q1=0,7; р2=0,5; q2=0,5; р3=0,6; q3=0,4;
р(х=0)=р1р2р3=0.7*0.5*0.4=0.14; р(х=1)=р 1q2q3+q1p2q3+q1 q2p3=0.41; Р(х=2)=0.36; Р(х=3)= 0.09.
Тогда закон распределения имеет вид:
| х | 0 | 1 | 2 | 3 |
| p | 0,14 | 0,41 | 0,36 | 0,09 |
Проверка:

Пример 2. В книге кулинарных рецептов имеется 6 рецептов приготовления первого блюда, 4 – второго блюда. Пять раз подряд выписывают наудачу взятые рецепты. Случайная величина Х – число рецептов первых блюд. Составить закон распределения величины Х.
Решение. Случайная величина Х может принимать значения Х=1, 2, 3, 4, 5.
Для расчета вероятностей применим классическое определение вероятности (p(A)=m/n) и формулы комбинаторики:
 ;
;
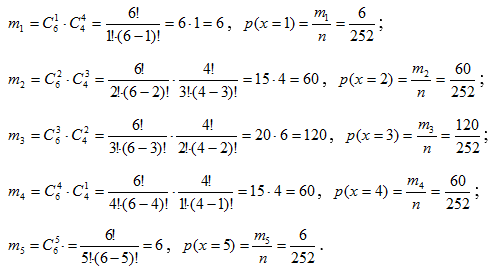
Закон распределения имеет вид:
| х | 1 | 2 | 3 | 4 | 5 |
| p | 6/252 | 60/252 | 120/252 | 60/252 | 6/252 |
3. Непрерывные случайные величины.
Случайной непрерывной величиной называется такая случайная величина, которая может принимать любые значения из конечного или бесконечного интервала. Например, размер детали массового производства; время ожидания автобуса на остановке; рост любого встреченного человека.
Непрерывная случайная величина задается либо функцией распределения вероятностей F(x), либо функцией плотности распределения вероятностей
f(x).
Функция распределения F(x) – это функция определяющая вероятность того, что случайная величина Х в результате испытания примет значение, меньшее

Свойства функции распределения F(x):
1. F(x) – неубывающая функция.
2.
3.

Функция плотности распределения f(x) – это функция, равная первой производной от функции распределения

Свойства плотности распределения f(x)
1. Плотность распределения – неотрицательная функция.

2. Несобственный интеграл от плотности распределения в пределах от - ¥ до ¥ равен единице.

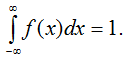
3. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b.
Пример 3. Случайная величина Х задана интегральной функцией распределения


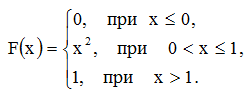
Найти дифференциальную функцию (плотность вероятностей).
Решение. 1) Перейдём от функции F(x) к функции f(x) по определению


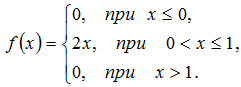
Пример 4. Случайная величина подчинена закону распределения с плотностью:

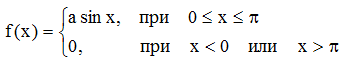
Найти:
-
коэффициент а, -
вероятность того, что случайная величина попадет в интервал от 0 до
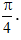
-
составить функцию распределения F(x).
Решение.
а) Для нахождения коэффициента а воспользуемся свойством


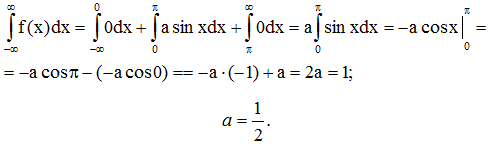
Тогда функция примет вид:
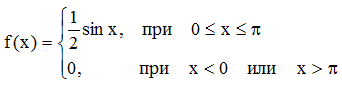

б) Находим вероятность попадания случайной величины в заданный интервал по формуле:

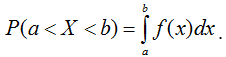

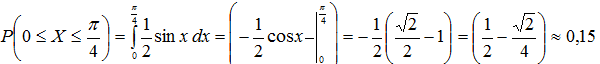
в) Для перехода от функции f(x) к функции F
(x) используем свойство 3 функции распределения


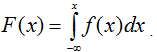
Тогда,