ЛАБОРАТОРНАЯ РАБОТА №2.

МОДЕЛИРОВАНИЕ СЛУЧАЙНОГО БЛУЖДАНИЯ
Цель: изучить средства электронных таблиц длямоделирования случайного изменения состояния объекта.

Постановка задачи

Изменение состояния объекта связано с изменением значений двух параметров – координат 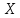и 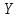, которое происходит случайно и дискретно: каждый параметр может остаться неизменным либо изменить свое значение на +1 или -1.

Таким образом, возможна реализация девяти взаимоисключающих событий, которые образуют полную группу:

(X,Y);	(X,Y+1);	(X,Y-1);
(X+1,Y);	(X+1,Y+1);	(X+1;Y-1);
(X-1;Y);	(X-1,Y+1);	(X-1,Y-1).

Вероятность изменения каждого параметра задана: PX_a, PX_b, PX_c; PY_a, PY_b, PY_c, при этом PX_a+PX_b+PX_c=1; PY_a+PY_b+PY_c=1. Таким образом, для каждого параметра возможны следующие события:

А – параметр остался неизменным;

В – параметр изменился на +1;

С - параметр изменился на -1.

Изменение значения каждого параметра происходит независимо от других.

Требуется построить компьютерную модель реализации случайного блуждания и исследовать поведение объекта.

Порядок выполнения работы

1. 
   Для решения задачи необходимо построить электронную таблицу по рис.3.
   

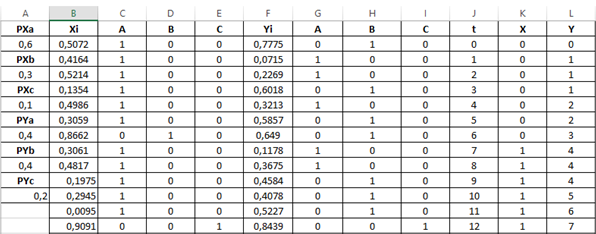
Рисунок 3 – Фрагмент таблицы моделирования

случайного блуждания (MS Excel)

Исходными данными для модели являются вероятности реализации событий А, В, С: PX_a, PX_b, PX_c; PY_a, PY_b, PY_c.

При моделировании случайных событий изменения Х и Y используются отдельные датчики случайных чисел на основе функции СЛЧИС(). В таблице X_i и Y_i – случайные числа. Появление событий А, В, С задается с использованием функции распределения аналогично дополнительному заданию из лаб.1.

В столбцах К и L вычисляются координаты точки в соответствии с постановкой задачи. Начальные значения: Х=0; Y=0. Значения координат в следующие моменты времени вычисляются по формулам:

---

Ячейка К3 =ЕСЛИ(C2=1;K2;ЕСЛИ(D2=1;K2+1;K2-1)).

Ячейка L3 =ЕСЛИ(G2=1;L2;ЕСЛИ(H2=1;L2+1;L2-1)).

2. 
   По результатам моделирования постройте временную диаграмму изменения точки (X;Y) (рис.4).
   

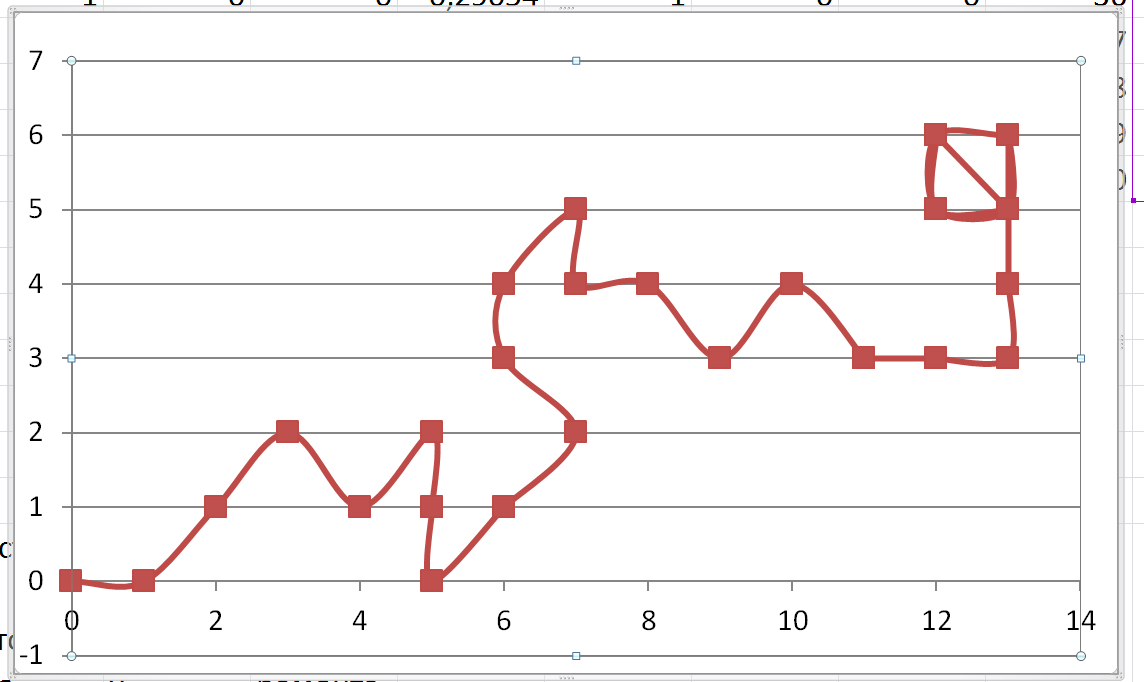
Рисунок 4 – Фрагмент временной диаграммы результата моделирования блуждания (MS Excel)

3. 
   Проведите серии экспериментов при разных значениях вероятностей событий и понаблюдайте, как изменяются получаемые диаграммы. (Пересчет формул производится при нажатии клавиши F9.)
   

---

Смотрите также файлы

• Расчет аренды за 2023 год арендатор Некоммерческая организация Лодочная станция Нептун Адрес земельного участка.docx

• Дневник педагогической практики.docx

• Инструкция Внимательно прочитайте текст и правильно выполните задания к тексту.docx

• "Эргырон" даст благотворительный концерт в поддержку участников спецоперации.docx

• Проблемы перевода художественного произведения, на примере произведения сары пеннипакер клементина.docx