МИНИСТЕРСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ

ПО ДЕЛАМ ГРАЖДАНСКОЙ ОБОРОНЫ, ЧРЕЗВЫЧАЙНЫМ СИТУАЦИЯМ

И ЛИКВИДАЦИИ ПОСЛЕДСТВИЙ СТИХИЙНЫХ БЕДСТВИЙ
Академия Государственной противопожарной службы
Кафедра организации деятельности пожарной охраны

Курсовая работа
по дисциплине «Математические методы и модели управления

пожарно-спасательными службами»
Тема: «МАТЕМАТИКО-СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДЕЯТЕЛЬНОСТИ ПРОТИВОПОЖАРНОЙ СЛУЖБЫ ГОРОДА»

Выполнил: слушатель 4122ГмЗ группы института подготовки руководящих кадров Жаботинский Александр Валерьевич «__» ____________ 20__ г.

Проверил: доктор технических наук профессор кафедры Соколов Сергей Викторович «___» _____________20 ___ г.

Москва

2023

Оглавление

Введение………………………………………………………………….………………4

1. Анализ статистических закономерностей привлечения пожарной техники для обслуживания вызовов………………………………………………………………......6

2. Анализ статистических закономерностей распределения числа вызовов пожарных подразделений в городе по суткам…………………………………….…...9

3. Анализ статистических закономерностей распределения длительности обслуживания вызовов пожарных подразделений в городе………………………...12

4. Моделирование одновременной занятости пожарных автомобилей при обслуживании вызовов в городе………………………………………………………16

5. Обоснование числа пожарных автомобилей для обслуживания вызовов в городе на основании числа отказов в обслуживании вызовов………………………………17

Выводы………………………………………………………………………………….20

Литература………………………………………………………………………………22

---

Введение

Проблемы обеспечения пожарной безопасности, в данный момент, становятся все более актуальными и сложными. Основные резервы повышения эффективности деятельности пожарно-спасательных служб необходимо искать
в совершенствовании организации управления, и более широком привлечении общественности к обеспечению безопасности народного хозяйства страны.

Принцип научности управления в сфере пожарной охраны требует изучения закономерностей процесса функционирования пожарной охраны
и управления ее аппаратами и подразделениями, творческого использования этих закономерностей при рационализации существующих и разработке новых структур управления, организации процесса управления, подбора
и расстановки кадров.

Совершенствование организации и управления пожарно-спасательных служб предполагает предварительную, глубокую научную проработку, по возможности, всех организационно-управленческих проблем, которые практика
во всевозрастающих масштабах ставит перед работниками пожарной охраны. Современные нормативные положения и рекомендации пока еще далеки
от совершенства и не получили научного обоснования, что значительно затрудняет решение, проблемы повышения эффективности деятельности Государственной противопожарной службы и совершенствования управления, ею.

Для решения указанных и подобных им организационно-управленческих проблем необходимо развернуть комплексное научное исследование процесса функционирования пожарно-спасательных служб, включающее организационный, функциональный, территориальный и отраслевой аспекты этого процесса.

Решение современных организационно-управленческих задач связано
со сбором и обработкой огромных информационных массивов, с колоссальным объемом вычислений. Эту работу сейчас все успешнее выполняет новая вычислительная техника.

Таким образом, математические методы решения организационно-управленческих проблем нужно рассматривать как весьма эффективные методы,

которые, тем не менее, необходимо сочетать с другими методами, позволяющими
в совокупности с первыми получить остаточно обоснованные и практически приемлемые решения таких проблем.

Кроме того, известная ограниченность применения математических методов заключается в том, что любая математическая модель не в состоянии учесть все многообразие факторов и параметров, оказывающих существенное влияние

---

на изучаемые процессы и явления.

Достоверность полученных результатов при использовании математических методов управления зависит от правильности сделанных предпосылок и взятых
за основу исходных данных.

Цель курсовой работы – повышение эффективности деятельности пожарной охраны города.

Задачи курсовой работы:

1. Анализ статистических закономерностей привлечения пожарной техники для обслуживания вызовов;

2. Анализ статистических закономерностей распределения числа вызовов пожарных подразделений в городе по суткам;

3. Анализ статистических закономерностей распределения длительности обслуживания вызовов пожарных подразделений в городе;

4. Моделирование одновременной занятости пожарных автомобилей
при обслуживании вызовов в городе;

5. Обоснование числа пожарных автомобилей для обслуживания вызовов
в городе на основании числа отказов в обслуживании вызовов.


1. Анализ статистических закономерностей привлечения пожарной техники для обслуживания вызовов

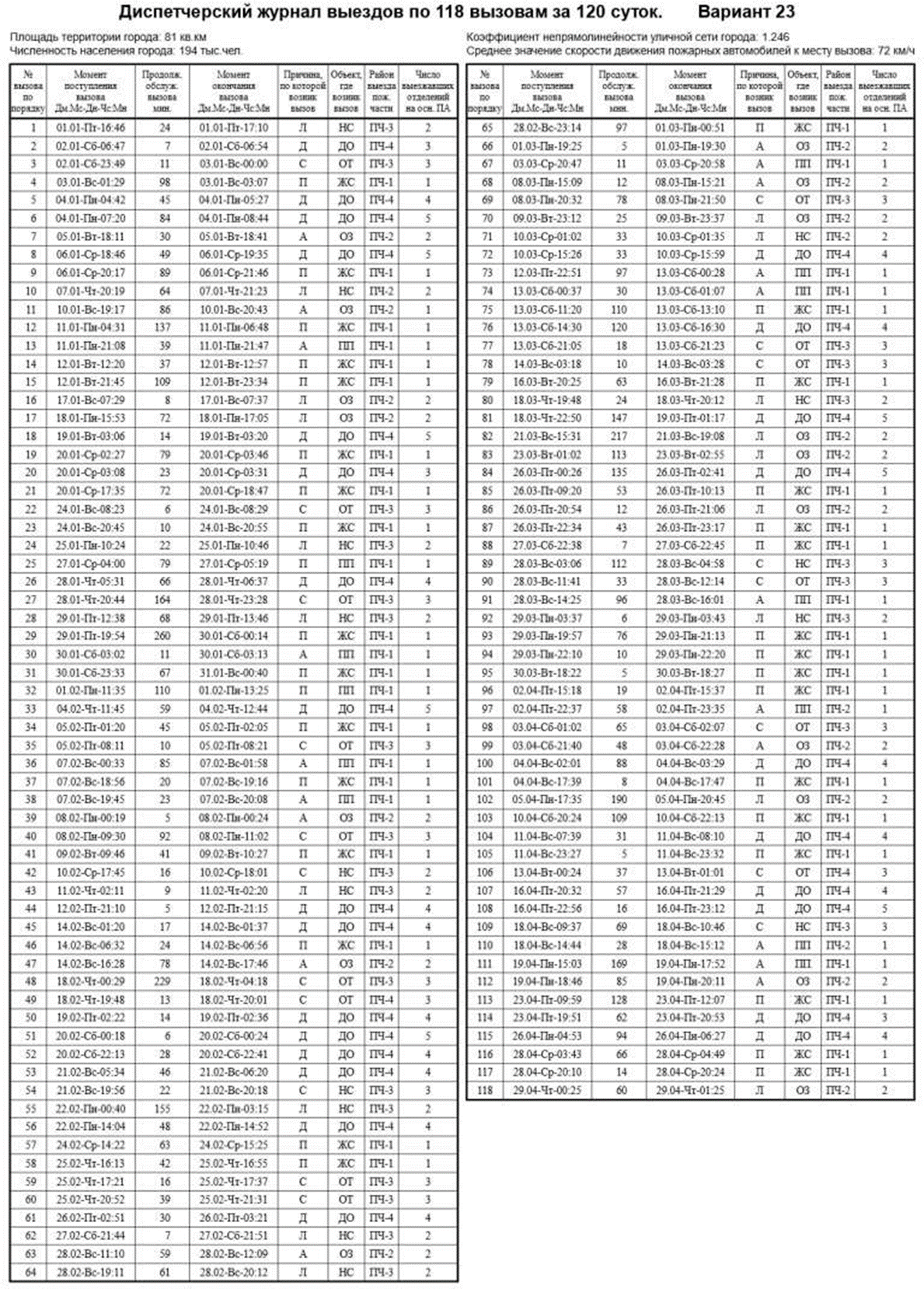
П 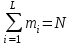о данным диспетчерского журнала находим число m_i вызовов
в городе, по которым выезжало определенное число i пожарных автомобилей
(i = 1,2,...,L, где L - максимальное число выезжавших по вызову пожарных автомобилей). Для полученных значений m_i, называемых абсолютными частотами, должно выполняться соотношение:

где N – общее число вызовов.

Производим вычисление доли ω_i, которую в общем числе вызовов составляют вызовы, для обслуживания которых привлекались i пожарных автомобилей (i = 1, 2,...,L):



Для полученных в результате вычислений значений ω_i (i = 1,2,…,L), называемых относительными частотами или частостями, должно выполняться соотношение:



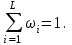
Перечень различных значений числа i выезжавших по вызову пожарных автомобилей (i = 1,2,...,L), каждому из которых поставлено в соответствие значение частоты m_i и частости ω_i, образует дискретный вариационный ряд, представленный в виде табл.1.

О 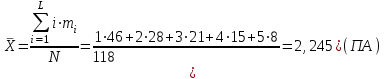пределим статистические характеристики данного вариационного ряда. Находим среднее число одновременно выезжающих пожарных автомобилей

---

по вызову (для представленного варианта):


Н 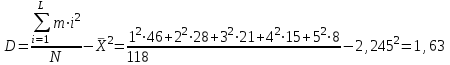аходим дисперсию вариационного ряда:


Н 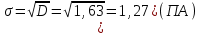аходим среднее квадратическое отклонение:
и 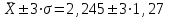спользуя правило «трех сигм», получаем
откуда следует, что размах вариаций будет находиться в пределах
от 0 до 6,05 автомобилей, выезжающих по вызову.

Для графического отображения распределения i выезжавших по вызову пожарных автомобилей в городе производится построение секторной круговой диаграммы (рис.1). Для построения диаграммы на круге произвольного диаметра с помощью транспортира выделяют секторы с центральными углами φ_i (i = 1,2,…,L), пропорциональными относительным частотам ω_i. Центральные углы вычисляются по формуле:



При этом достаточно ограничиться целыми значениями, так как при помощи транспортира затруднительно добиться точности до долей градуса. Полученные значения центральных углов вносятся в табл. 1. Для них должно выполняться соотношение:




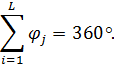
Таблица 1

Распределение числа пожарных автомобилей, выезжающих по вызовам

Количество ПА i	Число вызовов (абсолютная частота) mi	Относительная частота ωi	Центральный угол φi,
1	2	3	4
1	46	0,39	140,4
2	28	0,237	85,32
3	21	0,178	64,08
4	15	0,127	45,72
5	8	0,068	24,48
итого	118	1,000	360

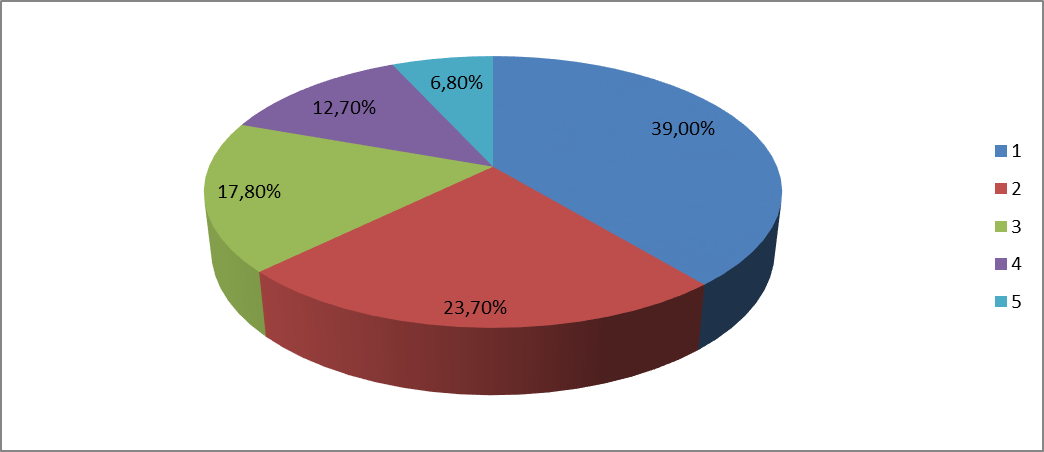
Рис.1 Секторная круговая диаграмма распределения числа пожарных автомобилей, выезжающих по вызовам

---

Выводы: на большинство вызовов выезжают 1 (39 %) и 2 (23,7 %) пожарных автомобилей.

2. Анализ статистических закономерностей распределения числа вызовов пожарных подразделений в городе по суткам
В течение периода наблюдения, зафиксированного в диспетчерском журнале и равного 120 суткам, определим эмпирическое и теоретическое распределение вызовов по суткам.

Для определения эмпирического распределения необходимо сделать следующее: по диспетчерскому журналу подсчитать число m_k суток
с определенным числом вызовов k (k = 0,1,2,…n). Вызовы, возникающие в течение одних суток, имеют одинаковые даты поступления. Для определения значения m₀ нужно посчитать число суток, даты которых отсутствуют в диспетчерском журнале, т.е. в эти сутки не произошло ни одного вызова.

П 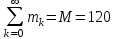олученные в результате подсчетов значения m_k называются эмпирическими частотами и связаны между собой соотношением:

Э 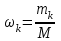мпирическая вероятность ω_k (относительная частота) того, что в интервале времени равным 1 суткам в городе произойдет k вызовов, оценивается как доля, которую в общем числе M суток составляет число суток, в течение которых произошло k вызовов:

Д 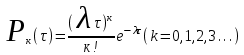ля определения теоретической вероятности того, что за время τ произойдет k выездов пожарных подразделений используем распределение Пуассона:

где λ – плотность потока вызовов, т.е. среднее число вызовов, поступающих за единицу времени τ, для нашего варианта λ=N/M=118/120=0,998 выз./сутки.


Проведем ряд расчетов теоретической вероятности для примерного варианта:








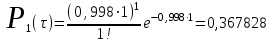
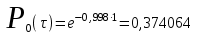
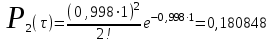
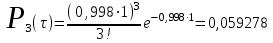
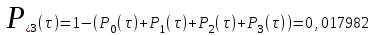
Д

---

Смотрите также файлы

• Законы термодинамики. Изопроцессы, их применение в медицине ( Презентация) Выполнил студент.pdf

• Реферат выполнил студент 1го курса гр. 112Б абдураимов Нурбекет Научный.docx

• Исходные данные Экономика некоторой страны характеризуется следующими показателями, представленными в таблице. Год.docx

• Есепті шарты.pptx

• Экономика и бухгалтерский учёт.doc