Добавлен: 17.03.2024
Просмотров: 15
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача.
Временные ряды
Имеются условные данные об объемах потребления электроэнергии (
Требуется:
1. Построить автокорреляционную функцию и сделать вывод о наличии сезонных колебаний.
2. Построить аддитивную модель временного ряда (для нечетных вариантов) или мультипликативную модель временного ряда (для четных вариантов).
3. Сделать прогноз на 2 квартала вперед.
Таблица 3.1 – Исходные данные
| | | | |
| 1 | 5,6 | 9 | 8,2 |
| 2 | 4,7 | 10 | 5,6 |
| 3 | 5,2 | 11 | 6,4 |
| 4 | 9,1 | 12 | 10,8 |
| 5 | 7,0 | 13 | 9,1 |
| 6 | 5,1 | 14 | 6,7 |
| 7 | 6,0 | 15 | 7,5 |
| 8 | 10,2 | 16 | 11,3 |
Решение:
1. Строим автокорреляционную функцию.
Автокорреляция уровней ряда – это корреляционная связь между последовательными уровнями одного и того же ряда динамики (сдвинутыми на определенный промежуток времени L – лаг). Лаг (сдвиг во времени) определяет порядок коэффициента автокорреляции. Если L = 1, то имеем коэффициент автокорреляции 1-го порядка. Если L = 2, то коэффициент автокорреляции 2-го порядка и т.д. Следует учитывать, что с увеличением лага на единицу число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается на 1. Поэтому обычно рекомендуют максимальный порядок коэффициента автокорреляции
, равный n/4. Рассчитав несколько коэффициентов автокорреляции, можно определить лаг (I), при котором автокорреляция (rt,t-L) наиболее высокая, выявив тем самым структуру временного ряда.
Осуществляем расчет коэффициента автокорреляции 1-го порядка. Предварительно сдвигаем исходный ряд на 1 уровень.
Таблица 3.2 – Расчетная таблица
| t | | | | | |
| 1 | 5,6 | 4,7 | 26,32 | 31,36 | 22,09 |
| 2 | 4,7 | 5,2 | 24,44 | 22,09 | 27,04 |
| 3 | 5,2 | 9,1 | 47,32 | 27,04 | 82,81 |
| 4 | 9,1 | 7,0 | 63,70 | 82,81 | 49,00 |
| 5 | 7,0 | 5,1 | 35,70 | 49,00 | 26,01 |
| 6 | 5,1 | 6,0 | 30,60 | 26,01 | 36,00 |
| 7 | 6,0 | 10,2 | 61,20 | 36,00 | 104,04 |
| 8 | 10,2 | 8,2 | 83,64 | 104,04 | 67,24 |
| 9 | 8,2 | 5,6 | 45,92 | 67,24 | 31,36 |
| 10 | 5,6 | 6,4 | 35,84 | 31,36 | 40,96 |
| 11 | 6,4 | 10,8 | 69,12 | 40,96 | 116,64 |
| 12 | 10,8 | 9,1 | 98,28 | 116,64 | 82,81 |
| 13 | 9,1 | 6,7 | 60,97 | 82,81 | 44,89 |
| 14 | 6,7 | 7,5 | 50,25 | 44,89 | 56,25 |
| 15 | 7,5 | 11,3 | 84,75 | 56,25 | 127,69 |
| 16 | 11,3 | 0,0 | 0,00 | 127,69 | 0,00 |
| Сумма | 118,5 | 112,9 | 818,05 | 946,19 | 914,83 |
| Среднее | 7,41 | 7,06 | 51,13 | 59,14 | 57,18 |
Рассчитываем выборочные дисперсии:
Рассчитываем среднеквадратические отклонения:
Линейный коэффициент автокорреляции 1-го порядка:
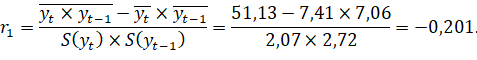
Таким образом, связь между рядами слабая и обратная.
Осуществляем расчет коэффициента автокорреляции 2-го порядка.
Таблица 3.3 – Расчетная таблица
| t | | | | | |
| 1 | 5,6 | 5,2 | 29,12 | 31,36 | 27,04 |
| 2 | 4,7 | 9,1 | 42,77 | 22,09 | 82,81 |
| 3 | 5,2 | 7,0 | 36,40 | 27,04 | 49,00 |
| 4 | 9,1 | 5,1 | 46,41 | 82,81 | 26,01 |
| 5 | 7,0 | 6,0 | 42,00 | 49,00 | 36,00 |
| 6 | 5,1 | 10,2 | 52,02 | 26,01 | 104,04 |
| 7 | 6,0 | 8,2 | 49,20 | 36,00 | 67,24 |
| 8 | 10,2 | 5,6 | 57,12 | 104,04 | 31,36 |
| 9 | 8,2 | 6,4 | 52,48 | 67,24 | 40,96 |
| 10 | 5,6 | 10,8 | 60,48 | 31,36 | 116,64 |
| 11 | 6,4 | 9,1 | 58,24 | 40,96 | 82,81 |
| 12 | 10,8 | 6,7 | 72,36 | 116,64 | 44,89 |
| 13 | 9,1 | 7,5 | 68,25 | 82,81 | 56,25 |
| 14 | 6,7 | 11,3 | 75,71 | 44,89 | 127,69 |
| 15 | 7,5 | 0,0 | 0,00 | 56,25 | 0,00 |
| Сумма | 107,2 | 108,2 | 742,56 | 818,50 | 892,74 |
| Среднее | 7,15 | 7,21 | 49,50 | 54,57 | 59,52 |
Рассчитываем выборочные дисперсии:
Рассчитываем среднеквадратические отклонения:
Линейный коэффициент автокорреляции 2-го порядка:
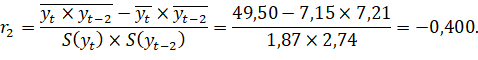
Таким образом, связь между рядами слабая и обратная.
Осуществляем расчет коэффициента автокорреляции 3-го порядка.
Таблица 3.4 – Расчетная таблица
| t | | | | | |
| 1 | 5,6 | 9,1 | 50,96 | 31,36 | 82,81 |
| 2 | 4,7 | 7,0 | 32,90 | 22,09 | 49,00 |
| 3 | 5,2 | 5,1 | 26,52 | 27,04 | 26,01 |
| 4 | 9,1 | 6,0 | 54,60 | 82,81 | 36,00 |
| 5 | 7,0 | 10,2 | 71,40 | 49,00 | 104,04 |
| 6 | 5,1 | 8,2 | 41,82 | 26,01 | 67,24 |
| 7 | 6,0 | 5,6 | 33,60 | 36,00 | 31,36 |
| 8 | 10,2 | 6,4 | 65,28 | 104,04 | 40,96 |
| 9 | 8,2 | 10,8 | 88,56 | 67,24 | 116,64 |
| 10 | 5,6 | 9,1 | 50,96 | 31,36 | 82,81 |
| 11 | 6,4 | 6,7 | 42,88 | 40,96 | 44,89 |
| 12 | 10,8 | 7,5 | 81,00 | 116,64 | 56,25 |
| 13 | 9,1 | 11,3 | 102,83 | 82,81 | 127,69 |
| 14 | 6,7 | 0,0 | 0,00 | 44,89 | 0,00 |
| Сумма | 99,7 | 103,0 | 743,31 | 762,25 | 865,70 |
| Среднее | 7,12 | 7,36 | 53,09 | 54,45 | 61,84 |
Рассчитываем выборочные дисперсии:
Рассчитываем среднеквадратические отклонения:
Линейный коэффициент автокорреляции 3-го порядка:
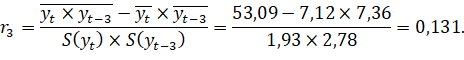
Таким образом, связь между рядами слабая и прямая.
Осуществляем расчет коэффициента автокорреляции 4-го порядка.
Таблица 3.5 – Расчетная таблица
| t | | | | | |
| 1 | 5,6 | 7,0 | 39,20 | 31,36 | 49,00 |
| 2 | 4,7 | 5,1 | 23,97 | 22,09 | 26,01 |
| 3 | 5,2 | 6,0 | 31,20 | 27,04 | 36,00 |
| 4 | 9,1 | 10,2 | 92,82 | 82,81 | 104,04 |
| 5 | 7,0 | 8,2 | 57,40 | 49,00 | 67,24 |
| 6 | 5,1 | 5,6 | 28,56 | 26,01 | 31,36 |
| 7 | 6,0 | 6,4 | 38,40 | 36,00 | 40,96 |
| 8 | 10,2 | 10,8 | 110,16 | 104,04 | 116,64 |
| 9 | 8,2 | 9,1 | 74,62 | 67,24 | 82,81 |
| 10 | 5,6 | 6,7 | 37,52 | 31,36 | 44,89 |
| 11 | 6,4 | 7,5 | 48,00 | 40,96 | 56,25 |
| 12 | 10,8 | 11,3 | 122,04 | 116,64 | 127,69 |
| 13 | 9,1 | 0,0 | 0,00 | 82,81 | 0,00 |
| Сумма | 93,0 | 93,9 | 703,89 | 717,36 | 782,89 |
| Среднее | 7,15 | 7,22 | 54,15 | 55,18 | 60,22 |
