Добавлен: 17.03.2024
Просмотров: 16
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рассчитываем выборочные дисперсии:
Рассчитываем среднеквадратические отклонения:
Линейный коэффициент автокорреляции 4-го порядка:
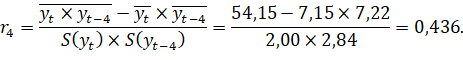
Таким образом, связь между рядами умеренная и прямая.
Таблица 3.6 – Корреляционная функция
| Лаг | Коэффициент автокорреляции |
| 1 | -0,201 |
| 2 | -0,400 |
| 3 | 0,131 |
| 4 | 0,436 |
Делаем вывод о наличии сезонных колебаний. Максимальный коэффициент автокорреляции 4-го порядка (0,430) свидетельствует о наличии сезонной компоненты в исследуемом ряду динамики.
2. Строим аддитивную модель временного ряда. Общий вид аддитивной модели следующий:
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент.
Осуществляем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
- найдем скользящие средние (гр. 3 табл. 3.7). Полученные таким образом выровненные значения уже не содержат сезонной компоненты;
- найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 4 табл. 3.7).
Таблица 3.7 – Оценка сезонной компоненты
| t | | Скользящая средняя | Центрированная скользящая средняя | Оценка сезонной компоненты (центрированная скользящая средняя - фактическое значение за период) |
| 1 | 5,6 | - | - | - |
| 2 | 4,7 | 5,2 | - | - |
| 3 | 5,2 | 6,3 | 5,8 | -0,55 |
| 4 | 9,1 | 7,1 | 6,7 | 2,38 |
| 5 | 7,0 | 7,1 | 7,1 | -0,08 |
| 6 | 5,1 | 6,0 | 6,6 | -1,45 |
| 7 | 6,0 | 7,1 | 6,6 | -0,57 |
| 8 | 10,2 | 8,1 | 7,6 | 2,58 |
| 9 | 8,2 | 8,0 | 8,1 | 0,13 |
| 10 | 5,6 | 6,7 | 7,4 | -1,77 |
| 11 | 6,4 | 7,6 | 7,2 | -0,77 |
| 12 | 10,8 | 8,8 | 8,2 | 2,62 |
| 13 | 9,1 | 8,9 | 8,8 | 0,28 |
| 14 | 6,7 | 7,8 | 8,3 | -1,62 |
| 15 | 7,5 | 8,5 | 8,1 | -0,63 |
| 16 | 11,3 | - | - | - |
Используем полученные оценки для расчета значений сезонной компоненты S. Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты Si. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Таблица 3.8 – Расчет сезонной компоненты
| Порядковый номер квартала | Порядковый номер квартала | |||
| 1 | 2 | 3 | 4 | |
| 1 | | | -0,55 | 2,38 |
| 2 | -0,08 | -1,45 | -0,57 | 2,58 |
| 3 | 0,13 | -1,77 | -0,77 | 2,62 |
| 4 | 0,28 | -1,62 | -0,63 | |
| Всего за период | 0,333 | -4,833 | -2,517 | 7,583 |
| Средняя оценка сезонной компоненты | 0,111 | -1,611 | -0,839 | 2,528 |
| Скорректированная сезонная компонента | 0,064 | -1,658 | -0,886 | 2,481 |
Исключаем влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины T + E = Y - S (гр. 4 табл. 3.9). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Таблица 3.9 – Расчет тенденции и случайной компоненты
| t | |
| 1 | 5,536 |
| 2 | 6,358 |
| 3 | 6,086 |
| 4 | 6,619 |
| 5 | 6,936 |
| 6 | 6,758 |
| 7 | 6,886 |
| 8 | 7,719 |
| 9 | 8,136 |
| 10 | 7,258 |
| 11 | 7,286 |
| 12 | 8,319 |
| 13 | 9,036 |
| 14 | 8,358 |
| 15 | 8,386 |
| 16 | 8,819 |
Таблица 3.10 – Результаты применения функции ЛИНЕЙН()
| Угловой коэффициент | 0,200 | 5,704 | Свободный член |
| Стандартная ошибка | 0,022 | 0,210 | Стандартная ошибка |
| Коэффициент детерминации | 0,859 | 0,401 | Стандартная ошибка регрессии S |
| F-статистика Фишера | 84,973 | 14 | Число степеней свободы v |
| Регрессионная дисперсия | 13,642 | 2,248 | Остаточная дисперсия |
Линейная функция тренда имеет вид:
Таким образом, аддитивная модель временного ряда выглядит следующим образом:
3. Прогнозируем на 2 квартала вперед:
