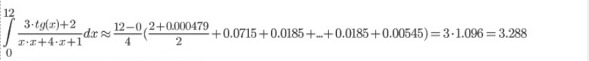Геометриялық мағынасы Фигураның ауданы ретінде 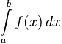анықталған интеграл сандық түрде х осімен, x = a және x = b түзулерімен және f(x) функциясының графигімен шектелген фигураның ауданына тең.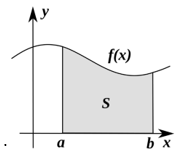



Сурет 1

Интеграция – интегралдың (немесе өрнектің) бірдей түрлендірулері және интегралдың қасиеттерін қолдану арқылы бір немесе бірнеше кестелік интегралдарға келтірілетін тікелей әдіс. Түрлері: · Тіктөртбұрыштар әдісі · Парабола әдісі (Симпсон формуласы) · Трапеция әдісі · Монте-Карло әдісі

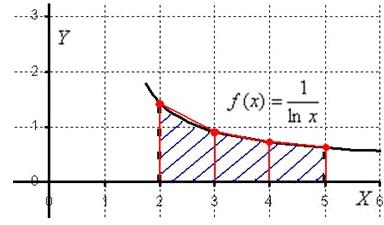
Трапеция әдісі. Интегралдау сегменті бірнеше аралық сегменттерге бөлінеді, ал интегралдың графигі сынық сызықпен жуықталады:



Сурет 2

Сонымен, біздің ауданымыз (көк көлеңке) трапециялардың (қызыл) аудандарының қосындысымен жуықталады. Әдістің аты осыдан шыққан. Трапеция әдісі тіктөртбұрыш әдісіне қарағанда (бөлу сегменттерінің бірдей санымен) әлдеқайда жақсы жуықтауды беретінін көру оңай. Және, әрине, біз неғұрлым кішірек аралық сегменттерді қарастырсақ, дәлдік соғұрлым жоғары болады. . Трапеция әдісінің мәні Өзімізге келесі тапсырманы қояйық: анықталған интегралды 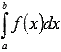шамамен есептеуіміз керек , мұндағы y=f(x) интеграл [a интервалында үзіліссіз; b].

Кесіндіні бөлейік [a; b] ұзындығы h нүктелері бар n тең интервалға . Бұл жағдайда қандай түйіндер теңдіктен анықталатын бөлу қадамы анықталады . Элементар интервалдардағы интегралды қарастырайық. Төрт жағдай мүмкін (суретте олардың ең қарапайымы көрсетілген, n шексіз өскен сайын барлығы азаяды):



Сурет 3

Әрбір кесіндіде

---

функциясын координаталары және нүктелері арқылы өтетін түзу кесіндімен y=f(x) ауыстырамыз. Біз оларды көк сызықтармен суретте бейнелейміз:



Сурет 4

Интегралдың жуық мәні ретінде 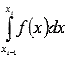өрнекті аламыз 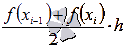, яғни қабылдаймыз .

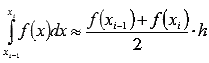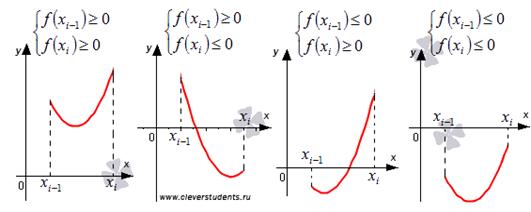
Жазылған жуықтық теңдік геометриялық мағынада нені білдіретінін анықтайық. Бұл сандық интегралдаудың қарастырылған әдісі неліктен трапеция әдісі деп аталатынын түсінуге мүмкіндік береді. Трапецияның ауданы табандарының қосындысының жартысының биіктігіне көбейтіндісі ретінде табылатынын білеміз. 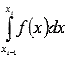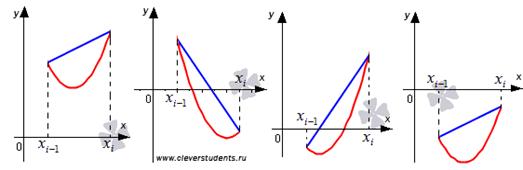Сондықтан бірінші жағдайда қисық сызықты трапецияның ауданы табандары мен биіктігі h болатын трапецияның ауданына шамамен тең, ал соңғы жағдайда анықталған интеграл шамамен а ауданына тең. минус белгісімен алынған табандары мен биіктігі h болатын трапеция. Екінші және үшінші жағдайларда анықталған интегралдың 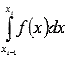жуық мәні төмендегі суретте көрсетілген қызыл және көк облыстардың аудандарының айырмасына тең.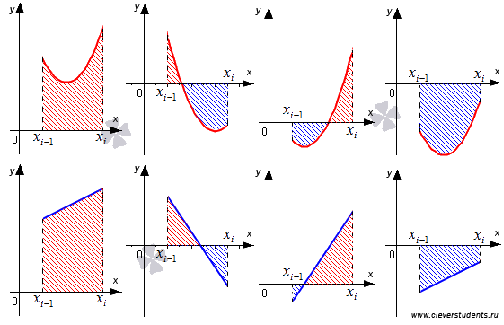



Сурет 5

Осылайша, біз трапеция әдісінің мәніне келдік, ол белгілі бір 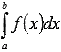интегралды әрбір элементар сегменттегі түрдегі интегралдардың 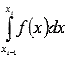қосындысы ретінде көрсетуден және кейінгі шамамен ауыстырудан тұрады.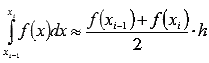

---

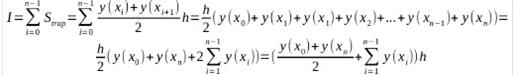
Трапеция әдісінің абсолютті қателігін бағалау Трапеция әдісінің абсолютті қателігі келесідей бағаланады.





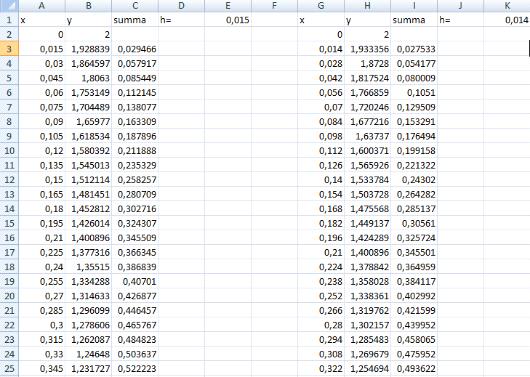
Сурет 6



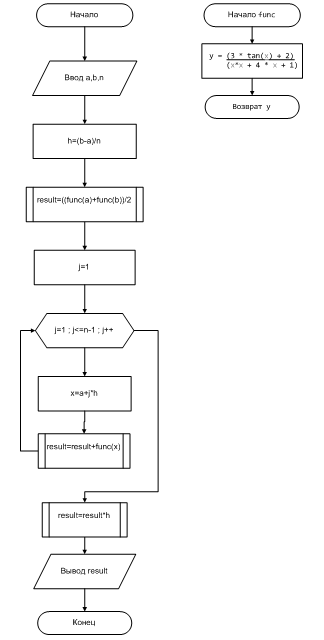
Сурет 7
#include

#include

using namespace std;

double func (double x)

{double y=(3*tan(x)+2)/(x*x+4*x+1);

return y;

}

int main()

{

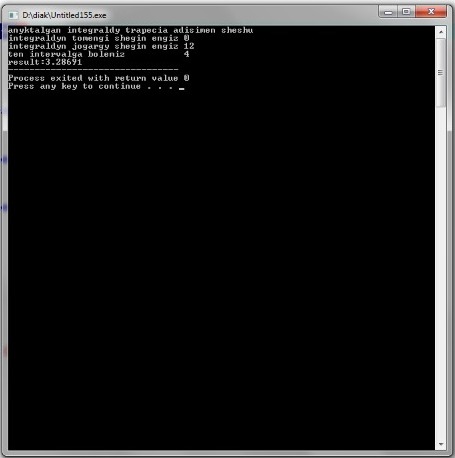
cout<<"anyktalgan integraldy trapecia adisimen sheshu";

cout<<"\n";

double a;

cout <<"integraldyn tomengi shegin engiz";

cin>>a;

double b;

cout <<"integraldyn jogargy shegin engiz";

cin>>b;

cout<<" ten intervalga bolemiz";

int n;

cin>>n;

{

double h = (b - a) / n;

double result = (func(a) + func(b)) / 2;

double x;

for(int j = 1; j <= n - 1; j++)

{x= a + j*h;

result = result + func(x); }

result = result*h;

cout<<”result:”<
return 0;

}}

---

Смотрите также файлы

• Тарихнама теориясы.docx

• Из генеральной совокупности извлечена выборка объема n. Найти среднее значение, дисперсию, среднее квадратическое отклонение, исправленную дисперсию, коэффициент вариации, моду и медиану.docx

• Лабораторная работа 2 по учебному курсу Цифровая культура.docx

• Пример входного файла.docx

• Основные причины травматизма во время занятий физической культурой.docx