Мазмұны

Кіріспе

1 Теориялық бөлім........................................................................

1.1 Құрылымдар мен біріктірулер...............................................

2 Тәжірибелік бөлім......................................................................

2.1 Тәжірибе барысында орындалған жұмыстар......................

2.2 Тестілеуші программа құру және нәтижесін алу.................

Кіріспе

Тәжірибеден өту кезінде біз С++ бағдарламалау жұмыс ортасында жұмыс жасадық.Өткен тақырыптарымызды пысықтап,оларға тіжәрибе барысында тапсырмаларды шығардық.

Менің жұмысымның тақырыбы С++ тіліндегі файлдарды қолдана отырып «Анықталған интегралды Симпсон әдісімен есептеу» қосымшасын құру.

Бұл жұмыста С++ тіліндегі файлдар,оны анықтау, онда құрылатын программалар мен операцияларға зерттеулер жүргіземін.

Зерттеу обьектісі: Анықталған интегралды Симпсон әдісімен есептеу

Жалпы ЭЕМ-ді қолдана отырып көптеген математикалық есептер шешілуде.Соның бірі математиканың бір бөлімі анықталған интеграл тақырыбын жуықтап есептеудегі шешімдерді С++ бағдарламалау тілі арқылы табуды қарастырып отырмыз.С++ тілі бұл С тілінің кеңейтілген түрі.

Ол құрылымдық программаларлы және күрделі есептеулерді құруға мүмкіндік береді.

Жүмыстың мақсаты:Анықталған интегралды жуықтап шешудің бірнеше әдістерін салыстыра отырып бағдарламалау,қателіктерді анықтау

1 Теориялық бөлім

ЭЕМ-нің жадында сандардың бір-бірімен байланысқан көптеген мәндерін сақтау үшін индексті айнымалылар, яғни массивтер қолданылады. Массив – бұлбір атаумен (массив идентификаторы) белгіленіп біріктірілген біртекті элементтер жиыны. Массивтердің негізгі парамтерлрі:

-          типі – массив элементтерінің жалпы типі (санды, символдық);

-          өлшемі – бірөлшемді, екіөлшемді;

-          көлемі – массив индекстерінің саны.

 

Нақты сандардан құрылған төмендегі тізбекті

1.2     14.6    -8.3     0.15     -9.85     7    5

бірөлшемді массив деп, оған А деген атау беруге болады.

Массивтерді өңдеу процесінде оның әр мүшесіне тура қатынас жасау үшін оны индекстеу (нөмірлеу) қажеттілігі туындайды.

Массивтің әр элементі массив атымен белгіленеді де, тік жақша ішіне оның индексі қойылады, яғни массив элементтері индекс бойынша реттеліп жазылады. Сондықтан оларды индекстелген айнымалылар дейді.



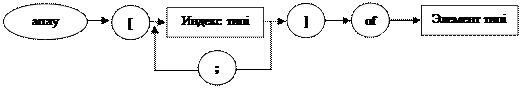
Егер программада массив қолданылса, онда ол айнымалылар 

---

Var бөлімінде немесе Type типтер бөлімінде сипатталуға тиіс:

1 тәсіл: Var бөлімінде сипаттау

Var <идентификатор>:array [индекс] of <элементтер типі>;

 

Var massiv : array [1.2, 4.6, -8.3, 0.15, -9.85, 7, 5] of real;

 

немесе a,b : array [1..40] of integer;

- 40 бүтін элементтен тұратын а және b массивтері берілген.

 

2 тәсіл: TYPE бөлімінде сипаттау

TYPE

     Типтің идентификаторы = array [T1] of T2;

VAR

     Массив идентификаторы : типтің атауы;

Мұндағы, Т1 – элементтер саны, Т2 – тип атауы.
1.1 Симпсон әдісі туралы түсінік

Геометриялық мағынасы Фигураның ауданы ретінде 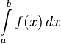анықталған интеграл сандық түрде х осімен, x = a және x = b түзулерімен және f(x) функциясының графигімен шектелген фигураның ауданына тең.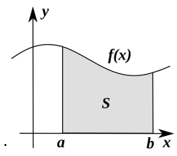



1-сурет.Функция графигі
Интеграция – интегралдың (немесе өрнектің) бірдей түрлендірулері және интегралдың қасиеттерін қолдану арқылы бір немесе бірнеше кестелік интегралдарға келтірілетін тікелей әдіс. Түрлері: · Тіктөртбұрыштар әдісі · Парабола әдісі (Симпсон формуласы) · Трапеция әдісі · Монте-Карло әдісі.

Симпсон әдісі (параболалық әдіс). Бұл неғұрлым жетілдірілген әдіс-интегралдық функцияның графигі сынған сызықпен емес, кішкентай параболалармен жақындайды. Қанша аралық сегменттер - сонша кішкентай параболалар. Егер сіз сол үш сегментті алсаңыз, онда Симпсон әдісі тіктөртбұрыш әдісіне немесе трапеция әдісіне қарағанда дәлірек жуықтауды береді.Сызба құруға көріп тұрғаным жоқ мағынасы, өйткені көзбен жақындауға болады накладываться арналған функциясының графигі (сынық сызық алдыңғы тармағының және онда іс жүзінде тұспа-тұс келді).



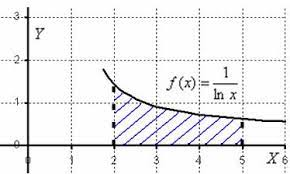
2-сурет. Функция графигі
Симпсон формуласы бойынша белгілі бір интегралды есептеу міндеті-практикадағы ең танымал тапсырма. Параболаның әдісіне көп көңіл бөлінеді.

Белгілі бір интегралды жуық есептеуге арналған Симпсон формуласы келесі формада болады:

---

- кішкентай сегменттердің әрқайсысының ұзындығы немесе қадамы;

- нүктелердегі интегралдық функцияның мәндері

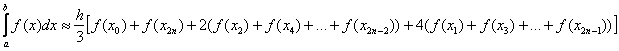
Бұл жинақты егжей-тегжейлі түсіндіре отырып,мен формуланы толығырақ талдаймын :

- интегралдық функцияның бірінші және соңғы мәнінің қосындысы;

- жұп индекстері бар мүшелер сомасы 2-ге көбейтіледі;

- тақ индекстері бар мүшелердің сомасы 4-ке көбейтіледі.

Параболалық әдістің мәні.

Әрбір интервалда 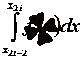интегралдық функция нүктелер арқылы өтетін квадраттық параболамен жақындайды . Демек, әдіс атауы-параболалық әдіс. Бұл Ньютон-Лейбниц формуласы бойынша есептей алатын белгілі бір интегралдың шамаланған мәні 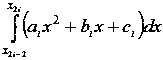ретінде алынады. Бұл параболалық әдістің мәні.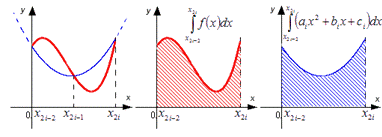


3-сурет.Параболаның графигі
Қызыл сызық y=f(x) функциясының графигін, көк сызық y=f(x) функциясының графигінің бөлінудің әр элементар сегментіндегі квадраттық параболалармен жуықтауын көрсетеді.



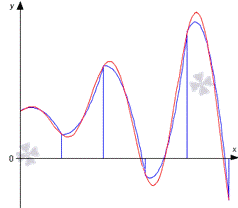
4-сурет.Квадраттық парабола графигі
S және m параметрлері олардың мәндерін арттыратын және төмендететін арнайы түймелермен реттеледі. Пайдаланушы пернетақтадан қажетті есептеу дәлдігін енгізеді. Бағдарлама параметрлері көрсетілген өрістер 5-суретте көрсетілген.

---

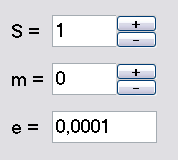
5-сурет.Есептеу дәлдігі

Бағдарламаның мысалы:



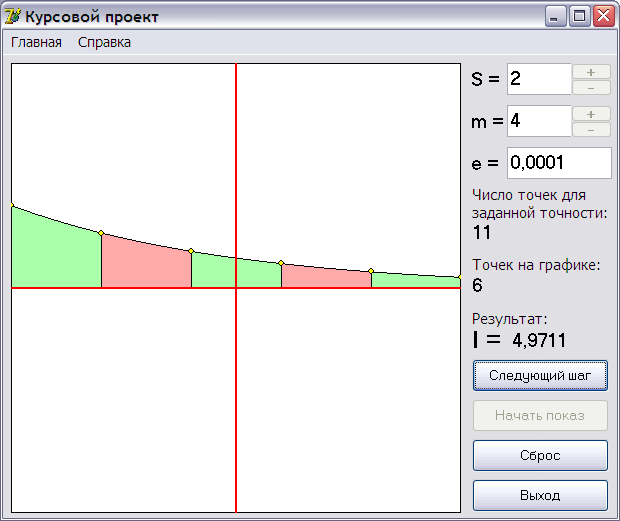
6-сурет.Симпсон әдісімен жасалған графика

Симпсон формуласы арқылы [Математикалық өңдеу қатесі] анықталған интегралды есептеңіз: [Математикалық өңдеу қатесі], мұндағы [Математикалық өңдеу қатесі] бөлінген сегменттер саны, [Математикалық өңдеу қатесі], [ Math Processing Error] — сегменттердің соңындағы мән функциялары.Сандық интегралдау есептерінде анықталған интегралды берілген дәлдікпен табу керек, ол үшін көрші жуықтаулар арасындағы айырмашылық көрсетілгеннен аз болғанша, интегралдау қадамын екі есе азайтқан сайын әдіс формуласы бойынша қайталап қате есептеу ұсынылады.

Функция	[Math Processing Error]a	[Math Processing Error]b	[Math Processing Error]eps	Интеграл	Комментарий
[Math Processing Error]f(x)=sin⁡(x2+2x)	1	3	0.0001	-0.143058	Тест пройден.
[Math Processing Error]ln⁡(1+x)	1	3	0.0001	2.15888	Тест пройден.
[Math Processing Error]tan⁡(3x3)	2	15	0.01	0.0256033	Тест пройден.
[Math Processing Error]x(x2−1)(x+1)	-1	1	0.3	-0.265625	Тест пройден.

7-сурет. Анықталған интегралды берілген дәлдікпен табу

Параболаның ауданын ені бірдей 6 төртбұрыштың аудандарын қосу арқылы табуға болады. Олардың біріншісінің биіктігі f (а), үшіншіден бесіншіге дейін - f (м), алтыншы - f (м) тең болуы керек. Осылайша, Симпсон әдісі бойынша жуықтау мына формула бойынша табылады:

---

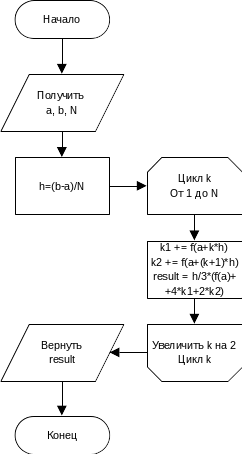
double simpsonIntegral (double a, double b, int n,) { const double width = (b-a)/n;

double simpson_integral = 0; for(int step = 0; step < n; step++) {

const double x1 = a + step*width; const double x2 = a + (step+1)*width;

simpson_integral += (x2-x1)/6.0*(f(x1) + 4.0*f(0.5*(x1+x2)) + f(x2));

} return simpson_integral; }
2 Тәжірибелік бөлім

Берілгені:





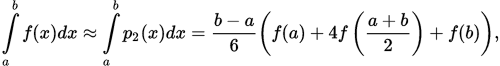
#include

#include

#include

using namespace std;

typedef double(*pointFunc)(double);

double f(double x) {

return (10 - x);

}

double simpson_integral(pointFunc f, double a, double b, int n) {

const double h = (b-a)/n;

double k1 = 0, k2 = 0;

for(int i = 1; i < n; i += 2) {

k1 += f(a + i*h);

k2 += f(a + (i+1)*h);

}

return h/3*(f(a) + 4*k1 + 2*k2);

}

int main() {

double a, b, eps;

double s1, s;

int n = 1; //бастапқы қадам саны

cout << “Sol jak integracia shegin engiz a = ";

cin >> a;

cout << "\ On jak integracia shegin engiz b = ";

cin >> b;

cout << "\Kajetti daldikti engiz eps = ";

cin >> eps;

s1 = simpson_integral(f, a, b, n); //Интеграл үшін бірінші жуықтау

do {

s = s1; //екінші жуықтау

n = 2 * n; //қадамдар санын екі есе көбейту

//қадам мәнін екі есе азайту

s1 = simpson_integral(f, a, b, n);

}

while (fabs(s1 - s) > eps); //берілген дәлдікпен жуықтауларды салыстыру

cout << "\nintegral = " << s1 << endl;

}
2.2 Тәжірибе барысында орындалған жұмыстар

1. 
   Берілген аралықта һ қадамымен х -тің өзгеру барысында төменде көрсетілген функцияның мәндерін тауып, осы мәндер бойынша кесте құрыңыздар:
   

Z=(x³+0.5x)/(2x-1), мұндағы х € [0,3 ; 0,8] hx=0.05

#include #include using namespace std; int main(){ float x=1; float y; while(x<=2){ Z=(x3+0.5x)/(2x-1); cout<<"x="< cout<<"y="< x=x+0.05;} return 0;}

X<=0.8 соңы X:=x+0.05 x,y ZZ=(x3+0.5x)/(2x-1) X:=0.3 басы

---

Смотрите также файлы

• Практическая работа 1 sql создание базы данных и таблиц Цель.docx

• Ввс св рвсн вмф пво.docx

• Обязанности.docx

• Интегралды жуы мні ретінде рнекті аламыз, яни абылдаймыз.docx

• Тарихнама теориясы.docx