Омский государственный технический университет

Кафедра физики

Отчёт

по лабораторной работе №1-18

ОПРЕДЕЛЕНИЕ СКОРОСТИ ПОЛЕТА ПУЛИ МЕТОДОМ БАЛЛИСТИЧЕСКОГО МАЯТНИКА

Выполнила:

студентка группы КЗИ-211

Богданович М. И.

Проверила: Суриков В. И.

____________________________________
Дата сдачи отчета: ____________________

Омск-2021

Лабораторная работа №1-18.

Определение скорости полета пули методом баллистического маятника.

Цель работы: примерить законы сохранения энергии и импульса для определения скорости полёта пули методом баллистического маятника
Краткая теория
Баллистическим маятником называется массивное тело, подвешенное на двух длинных параллельных нитях. При попадании пули в такой маятник нити обеспечивают поступательное (без вращения) отклонение маятника от положения равновесия.

Примем за систему два тела – маятник и пулю. Рассмотрим три состояния такой системы (см. рис.).

1) Маятник массы M неподвижен в положении равновесия. Пуля массы m подлетает к маятнику горизонтально со скоростью .

2) Пуля попала в маятник и в результате абсолютно неупругого взаимодействия застряла в нем. Маятник с застрявшей пулей получил некоторую скорость .

3) Маятник с застрявшей пулей отклонился на максимальный угол α. Его скорость в этот момент равна нулю.


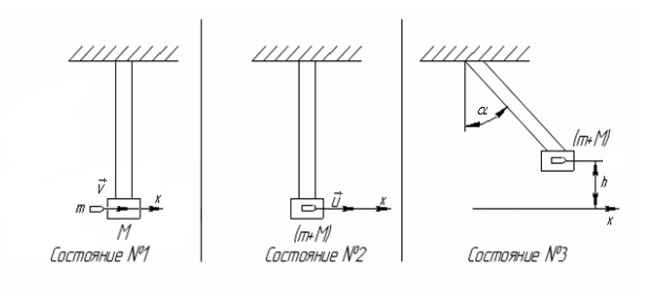
Состояния 1 и 2 можно связать законом сохранения импульса. Строго говоря, рассматриваемая система в момент взаимодействия не является замкнутой, так как на нее действуют внешние силы тяжести и упругости, причем сумма этих сил не равна нулю, что обеспечивает движение маятника по дуге окружности с некоторым нормальным ускорением. Однако, как известно, и для незамкнутой системы сохраняется сумма проекций импульсов тел на ту координатную ось, на которую внешние силы имеют нулевые проекции. В нашем случае такой осью является горизонтальная ось Х, направленная вдоль первоначальной скорости пули. Тогда получим

---

. Учитывая, что у нас v_x = v, u_x = u, имеем

(1)
Теперь свяжем между собой состояния 2 и 3. Так как на систему в этом случае действуют только консервативные силы тяжести и реакции (упругости) нитей, то полная механическая энергия системы должна сохраняться. Проведем нулевой уровень потенциальной энергии через центр масс системы в ее нижнем положении. Тогда закон сохранения энергии запишется следующим образом

(2)

После сокращений выразим величину u.



(3)

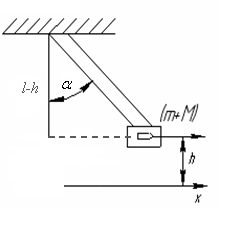
Высоту подъема маятника с застрявшей пулей легко выразить через угол отклонения маятника α (см. рис. ).

(4)
Подставив (4) в (3), получим
(5)
И наконец, подставляя (5) в (1), выражаем скорость полета пули v.
(6)

Таким образом, зная массу маятника M, массу пулиm, длину нитей подвеса l, и измеряя опытным путем максимальный угол α отклонения баллистического маятника после попадания пули, можно по формуле (6) рассчитать скорость полета пули.


Экспериментальная часть

Задать массу маятника и пули. Произвести моделирование движения пули и маятника при нажатии кнопок «Огонь» и «Зарядить». Провести пять экспериментов с выбранными параметрами. Данные эксперимента занести в таблицу 1.

Таблица 1

L, м	m, г	M, кг			Vп	ΔVп	ε, %
1	4	1	12,2	12,32	168,53	2,09	1,24
			12,4
			12,2
			12,4
			12,4

---

Студентка гр. КЗИ-211 Богданович М.И.

Дата выполнения 03.11.2021 Преподаватель Суриков В.И.

Обработка результатов измерений

1. 
   Найти среднее значение угла отклонения баллистического маятника в градусах.
   

2. 
   Определить абсолютную погрешность величины по правилам обработки результатов прямых измерений.
   

^°

3. 
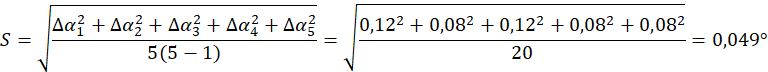
   Рассчитать скорость полета пули по формуле (6).
   

4. 
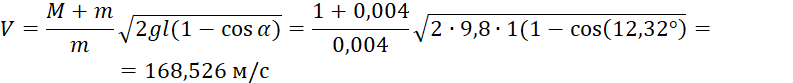
   Найти погрешности величины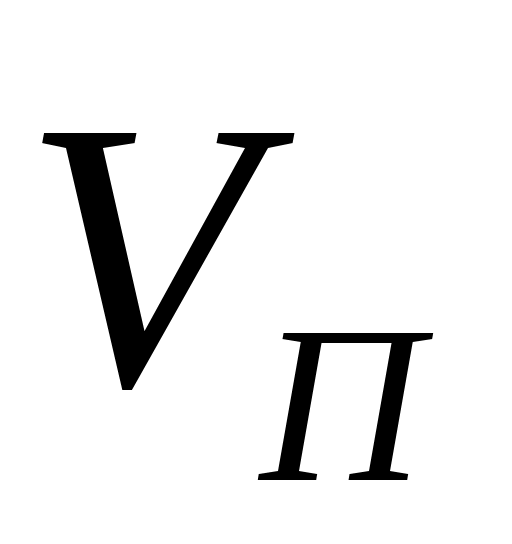 по правилам обработки результатов косвенных воспроизводимых измерений (погрешностями в определении всех величин, кроме , можно пренебречь).
   

---

Выводы

1. 
   В лабораторной работе определялась скорость полёта пули с помощью баллистического маятника.
   
2. 
   Измерялся угол отклонения баллистического маятника при попадании пули массой 4 г в маятник массой 1 кг.
   
3. 
   Рассчитаны угол отклонения баллистического маятника и скорость полёта пули:
   

Погрешность в определении угла отклонения баллистического маятника рассчитана по методике прямых многократных измерений.
Погрешность в определении скорости полёта пули рассчитана по методике косвенных однократных измерений.

---

Смотрите также файлы

• Протокол маршрутизации ospf использует метрику.docx

• аза тілі пні бойынша рефлексивті есеп 1 тосан.docx

• Кіріктірілген саба жоспары.docx

• геодезический контороль осадок зданий и сооружений промышленных предприятий.doc

• Практическая работа 2 (Часть 1).docx