МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНСТИТУТ ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

СПЕЦИАЛЬНОСТЬ «Финансы и кредит»
КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Финансовая математика»

Вариант № 70
Выполнил:

Студент 2 курса 4 семестра

(сокращенная форма обучения)

Зяблицева Лариса Леонидовна

Нижневартовск, 2010
Содержание



Для записи использованных для решения задач формул используются следующие обозначения:

P – первоначальный капитал (настоящая, современная стоимость);

S – наращенный капитал (будущая стоимость);

n – продолжительность финансовой операции в годах;

i – годовая ставка процентов;

d – учетная ставка;

τ – годовой уровень инфляции

I_τ – индекс инфляции



Задача 1.


Два платежа 4 млн. руб. и 3 млн. руб. со сроками через 4 и 6 лет (начала обязательств совпадают во времени) заменяются двумя платежами. Первый в размере 2 млн. руб. выплачивается через 2 года, второй платеж выплачивается через 5 лет. Найти размер второго платежа. При расчетах применить ставку сложных процентов 10% годовых.

Решение:

Наращение по ставке сложных процентов рассчитывается по формуле:

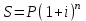
Сначала найдем сумму первых двух платежей:
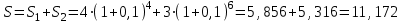млн. руб.
Вычислим сумму вторых двух платежей:
,

;

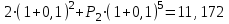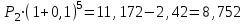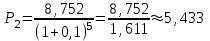млн. руб.
Ответ: размер второго платежа составит ≈5млн. 433 тыс. руб.

---

Задача 2


В контракте предусматривается при погашении обязательства через 5 лет уплатить 2,5 миллионов рублей. Первоначальная сумма ссуды 1,5 миллионов рублей. Определить доходность операции для кредитора в виде:

1) простой процентной ставки;

2) простой учетной ставки;

3) сложной процентной ставки;

4) сложной учетной ставки.

Решение

Определим доходность операции для кредитора в виде:

1) простой процентной ставки:
,

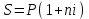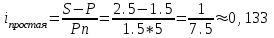или 13.3%.
2) простой годовой учетной ставки : ,
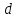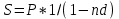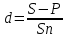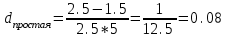; или 8%
3) сложной процентной ставки: ,
, , ,
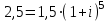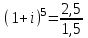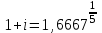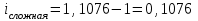
или 10,76%.

4) сложной учетной ставки: ,
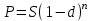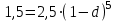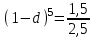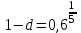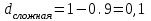, , , или 10%.




Задача 3


Есть возможность положить деньги либо на пенсионный вклад под 10% годовых, либо на вклад с ежемесячным начислением процентов по ставке 3% годовых. Какой вариант предпочесть? Срок вклада 10 месяцев.

По первому варианту вклада

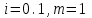
По второму варианту вклада

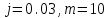
Рассчитаем значение эффективной ставки процентов для второго варианта. Значение эффективной ставки процентов находится по формуле:


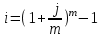
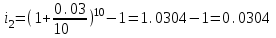или ≈3,04 % годовых
То есть i₁=10% > i₂ = 3,04% , 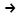первый вариант размещения сбережений во вклад выгоднее для кредитора при прочих равных условиях.

Ответ: первый вариант вклада выгоднее.

---

Задача 4


На сумму 1,5 млн. руб. в течение 2 лет начисляются сложные проценты по ставке 7% годовых. Прогнозируется, что темп инфляции будет постоянен и равен 1% в месяц. Найти наращенную сумму с учетом обесценения.

Решение

Наращенная сумма вклада
S = P*(1+ni) = 1.5*(1+2*0.07) = 1, 71 млн. руб.
Индекс инфляции за срок хранения вклада составит
J_τ = (1 + 0,01)² = 1,0201
Реальная сумма вклада
S_τ = 1,71 / 1,0201 = 1,6763 млн. руб.
Ответ: наращенная сумма с учетом обесценения 1,6763 млн. руб.

Задача 5

процент вклад ставка кредит

Кредит в 10 млн. pyб. выдан на 2 года. Реальная доходность должна составлять 4% годовых (сложные проценты). Расчетный уровень инфляции 2% в год. Определить ставку процентов при выдаче кредита, обеспечивающую полную компенсацию инфляции, а также наращенную сумму.

Решение

Ставка сложных процентов, обеспечивающая реальную эффективность кредитной операции в условиях инфляции, рассчитывается по формуле:
,
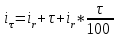где τ – годовой уровень инфляции, i_r– реальная доходность кредита.

По условию задачи,
%.
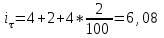Рассчитаем погашаемую сумму с учетом инфляции:
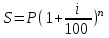
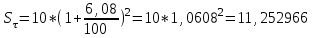млн.руб.

Ответ: ,


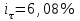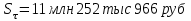
Задача 6


Внешнеторговому объединению при покупке товаров был предоставлен кредит в размере 240 млн. руб. под 4% годовых. По взаимной договоренности решено погасить этот кредит единовременной выплатой через 4 года. С этой целью образован фонд, в который ежегодно вносятся 40 млн.руб. Годовая эффективная процентная ставка банка, где хранится фонд, равна 3%. Найти сумму, которую следует добавить к фонду, чтобы погасить кредит через указанный срок.

Решение
Определим наращенную сумму:
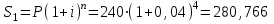млн. руб.
Найдем сумму, накопленную в фонде накопления на конец срока выплаты, по формуле финансовой ренты:

---

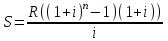
В фонд ежегодно вносятся 40 млн.руб., то есть 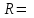40.
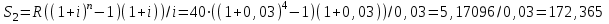млн. руб.

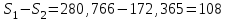млн. руб.
Ответ: сумма, которую следует добавить к фонду, чтобы погасить кредит через указанный срок = 108 млн. руб.

Задача 7


Долг в размере 10000 ден. ед. решено погасить частями в течение 2 лет. Выплаты производятся в конце каждого полугодия. Проценты начисляются раз в конце года по ставке 4% .Найти размер платежа.
Решение

Задача решается по формуле финансовой ренты.
→
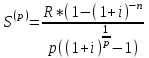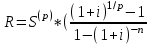
Определим размер полугодового платежа.
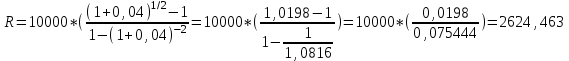ден. ед.

Ответ: размер платежа 2624,463 ден. ед.

Задача 8


Предлагается сдать в аренду участок на 3 года. Имеются следующие варианты оплаты аренды:

1. 
   12 миллионов рублей в конце каждого года,
   
2. 
   40 миллиона рублей в конце последнего года,
   
3. 
   12 миллионов рублей в начале каждого года.
   

Какой вариант более предпочтителен, если банк предлагает 3% годовых по вкладам?

Решение

1) Оплата 12 млн. руб. в конце каждого года – финансовая рента постнумерандо. Общая сумма за 3 года – это наращенная сумма финансовой ренты, которая рассчитывается по формуле:
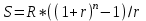
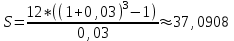млн. руб.
2) Единовременная оплата аренды в конце срока аренды – это финансовая рента с периодом, превышающим год, исчисляется по формуле:
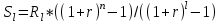, где l – период, превышающий 1 год, l=3

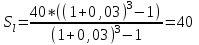млн. руб.
3) Оплата 12 млн. руб. в начале каждого года – финансовая рента пренумерандо


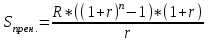
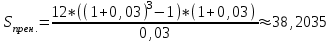млн. руб.
Ответ: Единовременная оплата аренды в размере 40 миллиона рублей в конце последнего года является предпочтительной.



Задача 9


Сравнивается два варианта строительства некоторого объекта. Первый требует разовых вложений в сумме 3 млрд. рублей и ежегодных вложений по 0,5 млрд.

---

Для второго затраты на создание равны 5 млрд. рублей и ежегодные взносы по 0,3 млрд. рублей. Продолжительность инвестиций 10 лет, процентная ставка – 12% годовых.


Какой вариант вложений выгоднее?

Решение.

Ежегодные взносы рассчитываются по формуле обыкновенной годовой финансовой ренты:

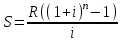
Рассмотрим первый вариант строительства:
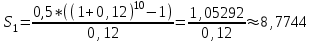млрд. руб.
S₁=3+8,7744≈11,7744 млрд. руб. – общий объем инвестиций за 10 лет в первом варианте строительства.

Рассмотрим второй вариант строительства.
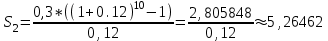млрд. руб.

S₂=5+5,26462≈10,26462 млрд. руб. - общий объем инвестиций за 10 лет

Второй вариант строительства имеет меньшую сумму инвестиций 10,26462<11,7744

Ответ: второй вариант строительства более выгоден.

Задача 10


В Сбербанк внесено 800 ден. ед. Этот вклад оставлен для начисления на него процентов по ставке 2 % годовых в течение 5 лет. Какую сумму можно снимать со счета ежегодно в течение последующих 10 лет (1 % годовых), чтобы последним изъятием закрыть счет?

Решение

Находим наращенную сумму: ,

где 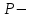первоначальная сумма, 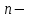число лет, 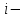процентная ставка.
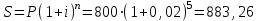ден. ед.
Так как амортизируются 883,26 ден. ед., то
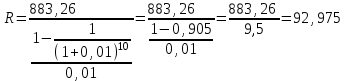ден. ед.
Ответ: в течение последующих 10 лет со счета можно снимать 92,975 ден. ед. ежегодно.

Задача 11


Ссуда в размере 1000 ден. ед. выдана на 130 дней под 3% годовых. Найти размер погасительного платежа, используя разные варианты начисления простых процентов.

Решение

Простые проценты начисляются по формуле
,
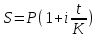где Р – первоначальная сумма долга, 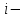ставка наращения процентов, t – число дней ссуды, K – число дней в году.

1.Точные проценты с точным числом дней ссуды

---

Смотрите также файлы

• Загрузите результат Индивидуального практического задания. 45 баллов, слушатель Ремизова Екатерина Олеговна Преподаватель Губарева Наталия Владимировна.doc

• Содержание индивидуального задания на практику в адвокатском образовании или юридической компании.docx

• Методические указания по написанию курсовых работ направление подготовки.docx

• Обзор правовых норм, относящихся к информации, правонарушения и меры их предупреждения.docx

• Сабаты таырыбы Табии радиоактивтілік. Радиоактивті ыдырау заы.docx