Добавлен: 18.03.2024
Просмотров: 9
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
Санкт-Петербургский горный университет
Кафедра общей физики
Отчет по лабораторной работе №13
По дисциплине: Физика
(наименование учебной дисциплины, согласно учебному плану)
Тема работы : определение коэффициента вязкости жидкости (методом Стокса)
Выполнил: студент гр.
(шифр группы) (подпись) (Ф.И.О)
Оценка:
Дата:
Проверил
руководитель работы: доцент
(должность) (подпись) (Ф.И.О)
Санкт-Петербург
2022
Цель работы: определить коэффициент вязкости жидкости методом Стокса.
Оборудование: большой цилиндрический сосуд с горизонтальными штрихами, исследуемая жидкость (касторовое масло), микроскоп МБС-9, свинцовые и стальные шарики
Теория необходимая для выполнения:
Вязкость(внутреннее трение) есть свойство текучих тел (жидкостей и газов)
оказывать сопротивление перемещению одного слоя вещества относительно другого.
Коэффициент вязкости – коэффициент, характеризующий данную жидкость.
Сила трения – сила, возникающая между соприкасающимися телами при их относительном движении.
Сила тяжести – сила, с которой тело действует на опору или растягивает подвес.
Выталкивающая сила (сила Архимеда) – сила, действующая на тело, погруженное в жидкость.
Ламинарное течение – течение, при котором вдоль потока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними.
Сила трения между плоскими слоями при их движении согласно з-ну Ньютона равна:
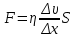
где - коэффициент пропорциональности, называемый коэффициентом вязкости или динамической вязкостью
; S - площадь соприкосновения слоев,
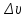- разница в скорости между соседними слоями, 
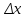- расстояние между соседними слоями.Соотношение силы трения шарика с его скоростью и радиусом при малых значениях скорости выражается следующей формулой:
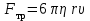,где
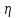- коэффициент вязкости, r- радиус шарика, 
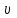- скорость движения шарика;По второму закону Ньютона:
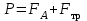
где Р- сила тяжести, действующая на шарик, FА- сила Архимеда, Fтр- сила внутреннего трения;
Сила тяжести вычисляется по формуле:
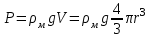,где м - плотность материала шарика; V – объем шарика;
Выталкивающая сила по закону Архимеда:
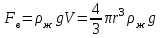
Схема установки.
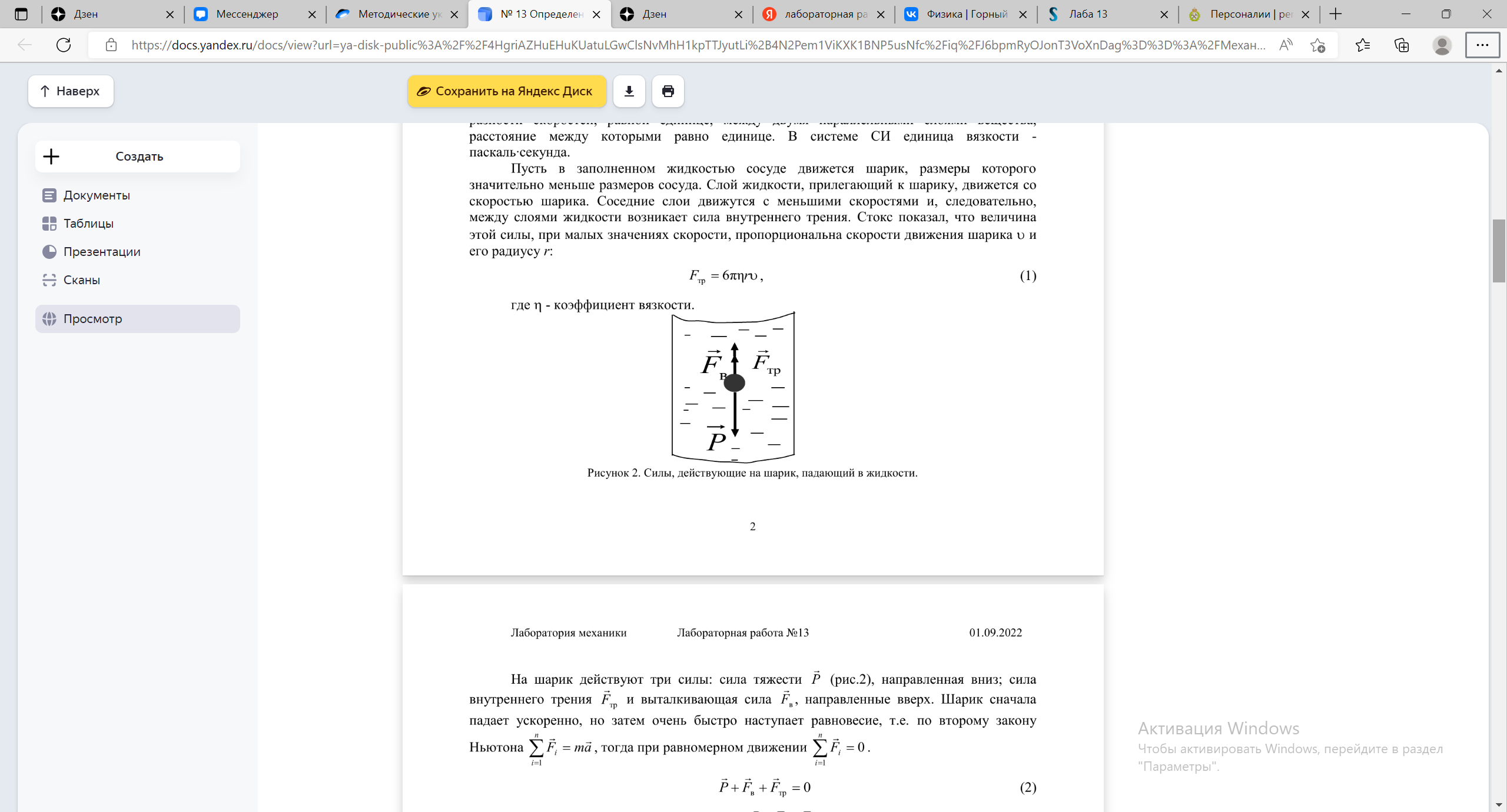
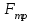- сила внутреннего трения, Н
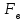- выталкивающая сила, НP – сила тяжести, Н
Основные расчетные формулы.
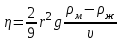
где
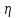- коэффициент вязкости, Па·сr - радиус шарика, м
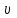- скорость движения шарика, м/с
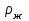- плотность жидкости, кг/м3
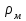- плотность материала шарика, кг/м3Формула расчета средней квадратичной погрешности.
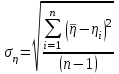
где
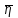- среднее значение коэффициента вязкости, 
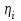- значение коэффициента вязкости в каждом отдельном опыте, n- количество опытов.Таблица измерений и вычислений.
| № | Т | ж | м | d | r | t | l |  | |  |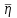
| Ед. | К | кг/м3 | кг/м3 | g | мм | с | м | м/с | Па·с | Па·с |
| 1 | 295,4 | 970 | 7800 | 21 | 1,785 | 4,55 | 0,2 | 0,044 | 1,077 | 1,08 |
| 2 | 295,4 | 970 | 7800 | 15 | 1,275 | 8,69 | 0,2 | 0,023 | 1,051 | 1,08 |
| 3 | 295,4 | 970 | 7800 | 18 | 1,53 | 6,4 | 0,2 | 0,031 | 1,123 | 1,08 |
| 4 | 295,4 | 970 | 11350 | 20 | 1,70 | 3,07 | 0,2 | 0,065 | 1,005 | 1,08 |
| 5 | 295,4 | 970 | 11350 | 75 | 1,88 | 2,82 | 0,2 | 0,071 | 1,125 | 1,08 |
| 6 | 295,4 | 970 | 11350 | 45 | 1,125 | 7,69 | 0,2 | 0,026 | 1,100 | 1,08 |
Погрешности прямых измерений:
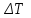=0,1К; 
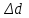1-4=17·10-6м; 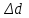5-6=5·10-6м; 
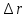= 5·10-5м; 
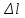= 10-3м; 
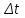=0,01с.Расчет результатов эксперимента.
1.пример расчета коэффициента вязкости:
=
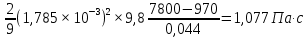
2. расчет среднего значения коэффициента вязкости жидкости:
=(η1+ η2+ η3+ η4+ η5+ η6)/6=(1,077+1,051+1,123+1,005+1,125+1,100)/6=1,08 Па·с.3. средняя квадратичная погрешность:
=
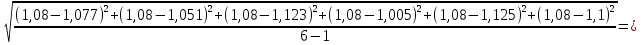0,046Окончательный результат:
= 1,08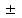
0,046 Па·сВывод: после проведения серии экспериментов и расчётов, я научился измерять коэффициента вязкости жидкости методом Стокса. Полученные данные немного отличаются от действительных, из-за эффекта параллакса при измерении времени погружения шарика, а также из-за неточности измерений радиуса шарика.