Файл: Самарский государственный университет путей сообщения.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 15
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
М
2358
инистерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Кафедра «Электрический железнодорожный транспорт»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению расчетно-графической (контрольной) работы по дисциплине
«Надежность ЭПС» для студентов специальности 190303
очной и заочной форм обучения
Составитель: И.П. Гордеев
Самара
2009
УДК 519.240.
Методические указания к выполнению расчетно-графической (контрольной) работы по дисциплине «Надежность ЭПС» для студентов специальности 190303 очной и заочной форм обучения / составитель : И.П. Гордеев. – Самара : СамГУПС, 2009. – 14 с.
Утверждены на заседании кафедры 22.04.2009 г., протокол № 8.
Печатаются по решению редакционно-издательского совета университета.
Методические указания содержат рекомендации к выполнению задач РГР (контрольной работы) по учебной дисциплине «Надежность ЭПС» специальности 190303 очной и заочной форм обучения.
Методические указания планируется использовать как при практических занятиях, так и при самостоятельной работе по решению задач, связанных с расчетом надежности деталей и узлов ЭПС.
Целью методических указаний является оказание помощи и выработка навыков студентами при решении задач по расчету надежности узлов и деталей локомотивов, а также закрепление знаний, полученных в лекционном курсе. Методические указания могут быть полезны работникам локомотивного хозяйства, связанным с эксплуатацией подвижного состава.
Составитель: Игорь Петрович Гордеев
Рецензенты: д.т.н., профессор кафедры «МПТ» СамГУПС В.М. Руцкой;
к.т.н., профессор кафедры «ЭЖТ» СамГУПС Н.Н. Капранов
Редактор И.М. Егорова
Компьютерная верстка Е.А. Самсонова
Подписано в печать 11.06.2009. Формат 60×90 1/16.
Усл. печ. л. 0,9. Тираж 150 экз. Заказ № 121.
©
Введение
Развитие и применение теории надежности как науки на железнодорожном транспорте особенно интенсивно проявилось в современных условиях, когда вопросы надежности деталей узлов и целых единиц подвижного состава тесно переплелись с экономической целесообразностью их изготовления, эксплуатации и ремонта.
После создания в рамках ОАО «РЖД» дорожных лабораторий надежности и отделов при проектно-конструкторских бюро, в которых данные об отказах узлов и деталей электровозов собираются и анализируются, появилась реальная возможность квалифицированно учитывать и активно влиять на надежность локомотивов в целом на всех стадиях их проектирования, изготовления и эксплуатации.
Использование имеющихся данных о наработках этих узлов до их отказов предполагает умение не только их анализировать, но и применять для прогнозирования и расчета времени безотказной работы локомотивов в периодах между регламентными работами.
Наиболее актуальным это стало в наши дни, когда все большее развитие получает идея проведения этих регламентных работ (техобслуживания и ремонта) в зависимости от технического состоянии подвижного состава. Внедрение такой системы невозможно без учета и прогнозирования сроков службы всего многообразия деталей, узлов и локомотива в целом. При этом речь идет не только об оценке надежности узлов и деталей локомотивов, но и о надежности систем диагностики, с помощью которых можно определить их текущее техническое состояние.
В настоящих методических указаниях предлагается рассмотреть несколько типичных задач по расчёту надежности основных узлов тепловоза. При этом предполагается, что время безотказной работы этих деталей и узлов распределяется во времени их эксплуатации по разным математическим законам. В методических указаниях рассмотрены четыре наиболее часто встречающихся закона: биномиальный, экспоненциальный, гамма-распределение и нормальный.
Исходные данные для задач, наряду с приведенными в методических указаниях, могут быть взяты студентами по данным реальной эксплуатации ЭПС на филиале кафедры (ГУП «САМАРАТРАНСПРИГОРОД»).
Задача № 1
По данным эксплуатационных и ремонтных служб вероятность выхода из строя ТЭД в депо, эксплуатирующем электровозы, за одну поездку составляет p.
Определить методом перебора и проверить по максимуму функции распределения наиболее вероятное количество ТЭД, выходящих из строя в месяц, если известно, что за этот период электровоз делает в среднем n поездок.
Данные для решения задачи приведены в таблице 1.1.
1.1. Количество поездок локомотивов в месяц и вероятность выхода из строя ТЭД за одну поездку
| Последняя цифра шифра (студ. билета) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| n | 11 | 13 | 12 | 15 | 14 | 17 | 19 | 16 | 20 | 18 |
| р | 0,1 | 0,35 | 0,2 | 0,25 | 0,15 | 0,17 | 0,23 | 0,4 | 0,3 | 0,29 |
Методические указания к решению задачи № 1
По условиям задачи предлагается определить наибольшую вероятность выхода из строя определенного количества ТЭД при наперед заданном количестве поездок. Такая задача определения надежности ТЭД может быть решена с применением схемы биномиальных испытаний.
Согласно этой схеме вероятность того, что в k испытаниях (поездках) выйдет из строя k ТЭД запишется в виде:
Pm (K)=C nk pk qn-k, (1.1)
где C nk=
(1.2)q=1 – p. (1.3)
Максимум функции распределения вероятностей при биномиальном законе по (1.1) достигается при выполнении следующего равенства:
=1 (1.4)то есть при k=np – q .
Задача № 2
Имеются нижеследующие данные по эксплуатации ТЭД в период послегарантийного пробега локомотива. При этом известно, что в период гарантийного пробега (350,00 км) ТЭД из строя не выходили. Данные приведены в таблицах 2.1, 2.2.
Принимая закон распределения вероятностей отказов ТЭД экспоненциальным (пробег близок к гарантийному), определить:
1. Вероятность того, что за пробег L тыс. км отказов ТЭД на локомотиве не будет.
2. Вероятность того, что ТЭД на локомотиве придется менять точно 3 раза.
3. Вероятность того, что ТЭД придется менять не менее 3 раз.
4. Сколько ТЭД на локомотиве выйдет из строя за пробег L тыс. км.
2.1. Пробеги ТЭД до отказа
| Условные номера ТЭД | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Пробег, тыс. км | 350 | 400 | 450 | 360 | 420 | 560 | 700 | 600 | 710 | 610 |
| Условные номера ТЭД | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Пробег, тыс. км | 525 | 410 | 500 | 635 | 705 | 395 | 416 | 383 | 370 | 670 |
Примечание. Для выбора данных по своему варианту необходимо к данным пробега в табл. 2.1 прибавить две последние цифры шифра (студ. билета).
Например: шифр студента 964; пробег ТЭД № 1 – 414 тыс. км; ТЭД № 2 – 464 тыс. км.
2.2. Заданный пробег локомотива
| Последняя цифра шифра (студ. билета). | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| L,тыс. км. | 557 | 757 | 657 | 364 | 564 | 675 | 575 | 420 | 470 | 400 |
Методические указания к решению задачи № 2
В условиях задачи сказано, что в период гарантийного пробега отказов не было. Это означает, что все ТЭД с технологическими дефектами изготовления были отбракованы в процессе их испытания на стендах контрольно-испытательной станции завода-изготовителя. Это в свою очередь означает, что двигатели в период послегарантийного ремонта работают в зоне нормального износа, где величина опасности их отказа равна постоянной величине.
Для таких случаев, когда вероятность отказа не зависит от времени предшествующей работы (заданный пробег ТЭД в табл. 2.2 близок к гарантийному), а зависит только от длины интервала (пробега), надежность элемента (ТЭД) может быть рассчитана на основе экспоненциального закона распределения вероятностей.
1. В соответствии с этим законом вероятность безотказной работы ТЭД при пробеге L тыс. км может быть вычислена по формуле
P (t)=e- t, (2.1)
где
=
, (2.2)где
L0 =
. (2.3)В этой формуле значения Li берутся из табл. 2.1. Цифра в знаменателе соответствует числу рассматриваемых ТЭД.
Таким образом, в окончательном виде вероятность безотказной работы при пробеге L тыс. км запишется в виде:
P0 (L)=
. (2.4)2. Вероятность того, что ТЭД на электровозе придется менять точно 3 раза, запишется в виде:
P3 (L)=
e- L. (2.5) 3. Вероятность того, что ТЭД придется менять не менее 3 раз вычисляется по формуле
. (2.6)4. Вопрос, сколько ТЭД на локомотиве выйдет из строя за пробег L тыс. км, решается путем перебора вариантов с использованием формулы
, (2.7)где i – число интересующих нас ТЭД.
Задача № 3
Пусть средний пробег локомотива по депо за год составляет 1,05∙106 тыс. км. В поездках происходит n отказов двигателей из-за размотки бандажей. По результатам обследования выясняется, что во всех случаях размотки произошли вследствие разносного боксования ТЭД.
Определить вероятность того, что в депо за общий пробег локомотива L тыс. км отказов ТЭД по якорным бандажам не произойдет. Плечи обращения локомотивных бригад составляют по всем направлениям 200 км. Локомотивы 4-осные.
Данные общего пробега локомотивов L тыс. км для решения задачи необходимо взять из таблицы 2.2 предыдущей задачи. Данные по количеству отказов ТЭД в поездках приведенные таблице 3.1.
3.1. Количество отказов ТЭД в год из-за размотки бандажей
| Предпоследняя цифра шифра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| Количество отказов n, шт. | 10 | 9 | 12 | 11 | 8 | 7 | 6 | 5 | 13 | 4 |
Методические указания к решению задачи № 3
Из условия задачи видно, что искомая вероятность также может быть вычислена на основании применения экспоненциального закона распределения.
Однако по данным задачи время работы ТЭД может быть вычислено в дискретных единицах – числе поездок k.
Аналогом экспоненциального закона распределения для времени работы изделия, выраженного в дискретных единицах, служат геометрическое распределение. Применение этого распределения значительно упрощает решение задачи.
Вероятность безотказной работы ТЭД за время большее числа поездок k выражается либо формулой
P { > k }=(1-)k+1 , (3.1)
где – вероятность отказа ТЭД из-за размотки бандажа за одну поездку, либо формулой
P { > k}e-k . (3.2)
Формула (3.2) применима в случае, когда мало, k велико, а произведение k∙ находится в пределах 0,1 ÷ 20.
Вероятность отказа ТЭД из-за размотки бандажей в одной поездке, может быть вычислена как частость отказа:
=
(3.3)где N – количество двигателей, участвующих в поездках локомотива за год, определяемое из заданного среднего пробега и заданных плеч обращения локомотивов.
Задача № 4
Пусть имеются данные о времени безотказной работы моторно-якорных подшипников (см. табл. 4.1).
Определить вероятность безотказной работы за L тыс. км. Предполагается, что опасность отказа при эксплуатации локомотива остается постоянной.
4.1. Данные по отказам моторно-якорных подшипников
| Условные номера подшипников | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Пробег до отказа, тыс. км | 350 | 400 | 450 | 310 | 420 | 560 | 700 | 600 | 750 | 710 | 610 |
| Условные номера подшипников | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| Пробег до отказа, тыс. км | 525 | 400 | 500 | 600 | 700 | 750 | 760 | 765 | 770 | 775 | 780 |
Примечание. Для определения своего варианта исходных данных задачи необходимо к данным таблицы 4.1 прибавить две последние цифры шифра (студ. билета).
Пробег L тыс. км выбрать, используя данные таблицы 2.2 задачи № 2.
Методические указания к решению задачи № 4
Задача решается также с применением экспоненциального закона распределения времени безотказной работы. Однако в этой задаче предлагается параметр опасности отказа определить с использованием приведенных данных о безотказной работе подшипников с разбиением их на две группы. Одна из них – это значение i , оказавшиеся меньше некоторого фиксированного числа Θ ;другая – все прочие значение i .
Приведем пример решения задачи для пробега L=500 тыс. км с использованием данных о времени безотказной работы моторно-якорных подшипников, приведенных табл. 4.1.
-
Выберем значение Θ=600 тыс. км. -
Определим функцию mi (Θ) – число отказов до пробега Θ=600 тыс. км:
mi (Θ)=9.
-
Определим накопленную частость отказов
ν (Θ) =
(4.1)где N – общее число подшипников, приведенное в таблице 4.1.
ν (Θ)=
.-
Определим опасность отказов.
Т. к. P {τ ≤ Θ}=F (Θ)= ν (Θ), (4.2)
ν (Θ)=1-e- Θ, (4.3)
откуда будет равна
=
(4.4)=
.-
Вероятность безотказной работы за 550 тыс. км:
P (t)=e- t; (4.5)
P(550)=e-0,000876∙550=0,618.
-
Вероятность отказа за тот же пробег
q (t) =1 – P(t); (4.6)
q(550)=1 – 0,618=0,382.
Задача № 5
Данные о работе моторно-якорных подшипников приведены в табл. 5.1.
Определить параметры распределения и оценить вероятность безотказной работы подшипников в течение времени t=60∙103 часов и t=100∙103 часов.
5.1. Время безотказной работы моторно-якорных подшипников
| Услов. номер подшип-ника | Время безотказ-ной раб.; τi – ч∙103 | Услов. номер подшип-ника | Время безотказ-ной раб.; τi – ч∙103 | Услов. номер подшип-ника | Время безотказ-ной раб.; τi – ч∙103 | Услов. номер подшип-ника | Время безотказ-ной раб.; τi – ч∙103 | Услов. номер подшип-ника | Время безотказ-ной раб.; τi – ч∙103 |
| 1 | 16 | 11 | 46 | 21 | 58 | 31 | 67 | 41 | 79,5 |
| 2 | 19,5 | 12 | 47 | 22 | 60,5 | 32 | 68 | 42 | 84,5 |
| 3 | 28 | 13 | 48 | 23 | 62 | 33 | 68,5 | 43 | 88 |
| 4 | 33,5 | 14 | 49,5 | 24 | 63 | 34 | 69 | 44 | 89,5 |
| 5 | 34,5 | 15 | 20 | 25 | 63 | 35 | 70 | 45 | 97 |
| 6 | 38 | 16 | 52 | 26 | 63,5 | 36 | 71,5 | 46 | 103 |
| 7 | 39,5 | 17 | 53 | 27 | 64,5 | 37 | 72 | 47 | 108,5 |
| 8 | 41 | 18 | 54,5 | 28 | 65 | 38 | 74,5 | 48 | 124,5 |
| 9 | 43 | 19 | 55 | 29 | 66 | 39 | 75,5 | 49 | 134,5 |
| 10 | 43,5 | 20 | 57 | 30 | 66 | 40 | 72 | 50 | 137 |
Примечание. Для выбора исходных данных по своему варианту к данным таблицы 5.1 необходимо прибавить сумму двух последних цифр шифра (студ. билета).
Например: шифр студента 421; время безотказной работы подшипника № 1 – 19∙103 часов; подшипника № 2 – 22,5∙103 часов и т. д.
Расчеты произвести исходя из того, что процесс изнашивания и отказов подшипников отвечает схеме накапливающихся повреждений.
Методические указания к решению задачи № 5
Как доказано практическими исследованиями схеме накапливающихся повреждений отвечает гамма-распределение и нормальное распределение времени безотказной работы элементов.
Плотность гамма-распределения имеет следующий вид:
f (T)=
(5.1)где r – число повреждений, необходимых для возникновения отказов;
Г (r) – гамма-функция, определяемая формулой
Г (r)=
. (5.2)В свою очередь, плотность нормального распределения описывается формулой:
f (T)=
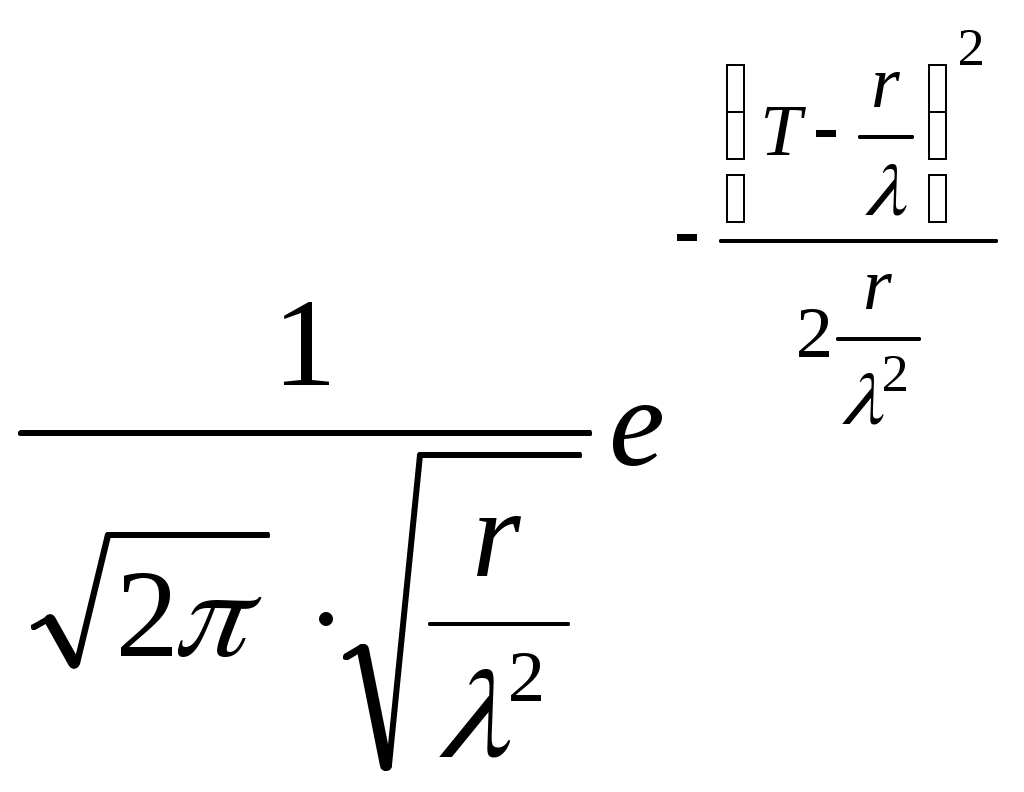. (5.3)В более общем виде формула (5.3) может быть представлена:
f (T)=
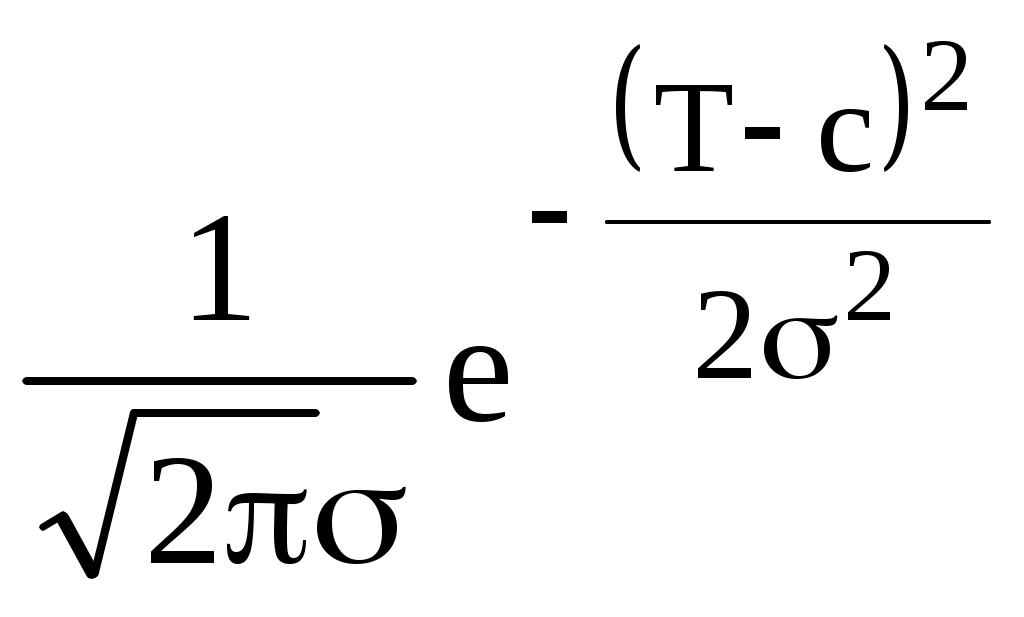, (5.4)где с и σ – параметры нормального распределения.
Параметр с численно равен математическому ожиданию распределения, а параметр σ2 равен его дисперсии, т. е.
M {τ}=c; (5.5)
D {τ}= σ2. (5.6)
Для гамма-распределения
M {τ}=
, (5.7)D {τ}=
. (5.8)Параметры λ и r могут быть оценены на основе данных о времени безотказной работы.
Пример. Пусть имеются данные о времени безотказной работы N объектов τ1 , τ2, ….. τN.
1. Находим эмпирическое среднее время безотказной работы
:
. (5.9)2. Находим дисперсию времени безотказной работы:
s
. (5.10)3. Приравнивая
=M {τ} и D {τ} =s
, получаем соотношения, из которых можно найти λ и r.
; (5.11)r=
. (5.12)Для нахождения вероятности безотказной работы в течение времени Т при целых r можно воспользоваться номограммой, приведенной в [2].
На вертикальной оси этой номограммы отложена вероятность безотказной работы, а по горизонтальной оси откладывается величина произведения λ∙Т. Каждая кривая номограммы отвечает своему значению r.
При решении этой задачи необходимо помнить, что переход от гамма-распределения к нормальному происходит, если отношение
, (5.13)то есть, если r >12.
Алгоритм решения задачи № 5 может быть выражен следующей последовательностью операций.
1. Найти эмпирические среднее и дисперсию времени безотказной работы.
; (5.14)
. (5.15)2. Определить опасность отказов λ и число повреждений r.
; (5.16)r=
.. (5.17)3. Определить произведения λ∙T1 и λ∙T2.
4. По номограмме для определения вероятностей безотказной работы, взятой из источника [2], определить функцию R (T)=P(τ > T).
5. Используя нормальное распределение, записать:
c=
; (5.18)σ=
. (5.19)6. Посчитать аргументы функции Лапласа.
X1 =
; (5.20)X2=
. (5.21)7. По таблице функции Лапласа, взятой из того же источника [2], определить Ф1 (X1) и Ф2 (X2).
8. Записать вероятность безотказной работы при нормальном законе распределения в виде:
P(τ > T)=1 – Ф (X). (5.22)
То есть P(τ > 60)=1 – Ф (X1); (5.23)
P(τ > 100)=1 – Ф (X2). (5.24)
Задача № 6
На ресурсные испытания корпусной изоляции якорей ТЭД ЭД118А были поставлены 1461 образец. По результатам испытаний была получена следующая таблица, характеризующая их надёжность.
6.1. Результаты наблюдений и исходные данные
для расчёта характеристик надёжности ТЭД ЭД118А
| Интервалы наработки | Показатели надёжности | ||
| Центр интервала t, тыс.км | Число работоспособных ТЭД в интервале N(t), штук | Число отказов в момент наработки t, n, штук | |
| 1 | 2 | 3 | 4 |
| 0 | 0 | 1461 | 0 |
| 1 | 50 | 1436 | 25 |
| 2 | 150 | 1393 | 43 |
| 3 | 250 | 1320 | 73 |
| 4 | 350 | 1216 | 104 |
| 5 | 450 | 1052 | 164 |
| 6 | 550 | 851 | 201 |
| 7 | 650 | 613 | 238 |
| 8 | 750 | 423 | 190 |
| 9 | 850 | 244 | 179 |
| 10 | 950 | 124 | 120 |
| 11 | 1050 | 61 | 63 |
| 12 | 1150 | 23 | 38 |
| 13 | 1250 | 0 | 23 |
Примечание. Для выбора исходных данных по своему варианту к данным таблицы 5.1, в столбце 3, начиная с первого интервала необходимо прибавить сумму двух последних цифр шифра (студ. билета). При этом соответственно изменятся значения четвёртого столбца.
Используя данные табл. 6.1, рассчитать количество запасных ТЭД, которыми должно располагать эксплуатационное предприятие для случаев их замены под локомотивами в данном регионе использования на среднюю наработку локомотивов по депо в 15 000 тыс. км с заданной вероятностью обеспечения замены Р = 0,99.
Методические указания к решению задачи № 6
Как показано в литературе [5], решение таких практических задач возможно с применением теории восстановления. При этом рекомендуется рассматривать ТЭД, как изделие с быстрым процессом восстановления. В соответствии с такой моделью требуемое количество ремонтов якорей ТЭД в электромашинном цехе депо за период эксплуатации t или число якорей ТЭД, которое должно быть на складе для их замены на локомотивах взамен вышедших из строя, равно
(6.1)где
– квантиль порядка Р нормального распределения, определяемого из условия 
;Т0 – математическое ожидание времени безотказной работы корпусной изоляции якорей ТЭД. Оно рассчитывается как статистическое значение среднего времени безотказной работы с использованием данных табл. 6.1 по формуле
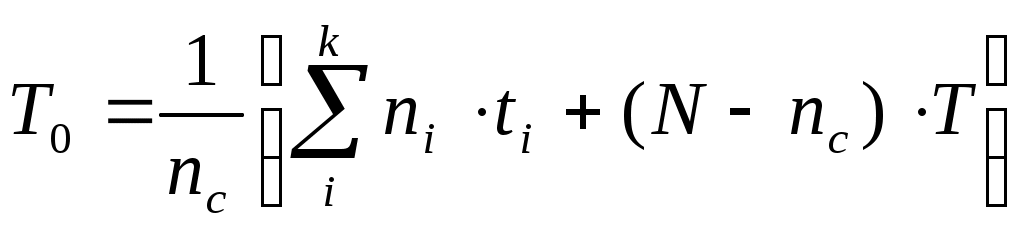, (6.2)где
– общее число отказавших ТЭД;k – общее число моментов наработки (число интервалов наработки);
i – 1,2,….., k – индекс наработки ТЭД в момент отказа;
ni – число отказов в момент наработки ti;
ti – момент наработки возникновения отказа (центр интервала наработки);
N – продолжительность наблюдений.
Подставив, например, в формулу (6.2) данные из табл. 6.1, получим
Т0 = 649,316 тыс. км,
– среднее квадратичное отклонение наработки ТЭД от среднего значения. Оно находится с использованием данных табл. 6.1 по формуле
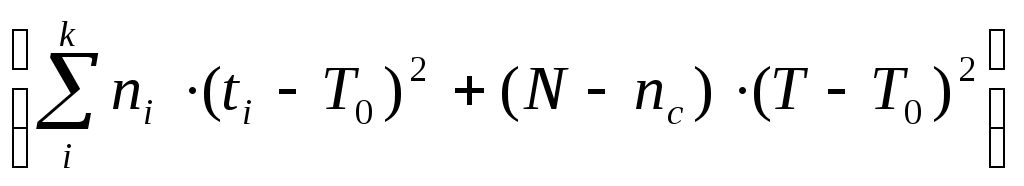. (6.3)Подставив в формулу (6.3) данные табл. 6.1, получим
66492,682 тыс. км.Далее, используя полученные данные и формулу (6.1), можно рассчитать для заданных условий задачи количество запасных ТЭД, которыми должно располагать эксплуатационное предприятие в данном регионе эксплуатации локомотивов. В частности, для данных табл. 6.1 оно равно
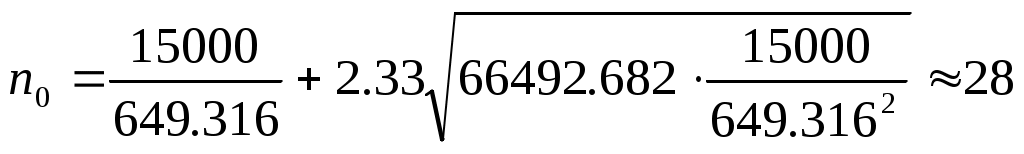ТЭД.Библиографический список
1. Гнеденко Б.В. Математические методы в теории надежности / Б.В. Гнеденко, Ю.К. Беляев, А.А. Соловьев. – М.: Наука, 1965. – 524 с.
2. Герцбац И.Б. Модели отказов / И.Б. Герцбац, Х.Б. Кордонский. – М.: Советское радио, 1966. – 166 с.
3. Вентцель Е.С. Исследование операций / Е.С. Вентцель. – М.: Советское радио, 1972. – 320 с.
4. Пустыльник Е.И. Статистические методы анализа и обработки наблюдений / Е.И. Пустыльник. – М.: Наука, 1968. – 288 с.
5. Гордеев И.П. Моделирование отказов изоляции обмоток тяговых электродвигателей локомотивов в эксплуатации : монография / И.П. Гордеев. – Самара : СамГУПС, 2006. – 172 с.