Добавлен: 19.03.2024
Просмотров: 9
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(k). доказано, что если не происходит вырождение матрицы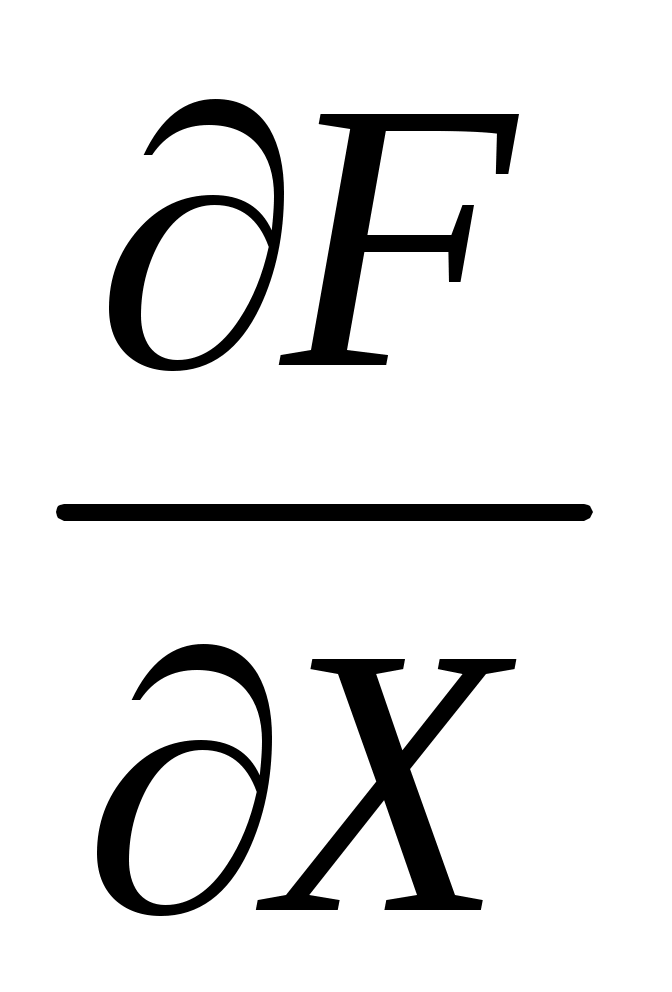 
, итерационная процедура (11) обеспечивает сходимость вычислительного процесса для любых существующих режимов вплоть до предельных, а при расчете несуществующих режимов процесс вычислений сходится к точке предельной гиперповерхности, где Якобиан системы УРР (предполагается, что пределы передаваемой мощности и устойчивости равны, т.е. вектор-функции F(X,Y) и W(X,Y) совпадают) равен нулю.
Суть способа непрерывного утяжеления можно пояснить на ходе итерационного процесса на плоскости двух параметров Y1 и Y2. При этом исходному режиму соответствует точка (Y1(0), Y2(0)), а утяжеление осуществляется изменением параметра Y2, то есть
Начальная величина параметра Т выбирается таким образом, чтобы выйти за пределы области устойчивости (существования рушения). После первой итерации происходит переход в точку, где вследствие неучета нелинейных членов разложения функции F(X,Y) в ряд Тейлора, кроме невязок по утяжеляемому параметру (Y2(н)-Y2(1)) появляется невязка по другой координате (Y1(1)-Y1(0)). По этой причине на второй итерации направление утяжеления изменяется, осуществляется переход в точку, где также имеет место отклонение от выбранной траектории Y(T), изменение направления утяжеления и т.д. При достижении предельной поверхности LF (LW) из-за наличия результирующих невязок по параметру Y1, не являющемуся утяжеляемым, возникает несоответствие между полученной точкой и искомой точкой. Поэтому появляется необходимость в уточнении решения. При этом вычислительный процесс, на каждой итерации которого невязка по утяжеляемому параметру полагается нулевой, проходит вблизи предельной поверхности, где матрица плохо обусловлена.
Можно обойтись без процесса уточнения одним из следующих способов.
Первый из них основан на дополнительной балансировке неутяжеляемых параметров режима при выходе их за пределы допустимых значений.
Другой способ связан с дополнительным, по сравнению с выбранным (11) , уменьшением шага. Этим обеспечивается требуемая степень соответствия результирующей точки вычислительного процесса и искомой предельной точки.
Однако, обе рассмотренные модификации приводят к нежелательному увеличению количества итераций. Общей причиной указанных осложнений является линеаризация УУР при использовании итерационной процедуры (11). Указанный недостаток можно устранить с помощью применения вычислительных методов [14, 29], которые позволяют увеличить шаг в выбранном направлении при обеспечении заданной точности по неутяжеляемым параметрам.
Они основаны на дополнительном учете нелинейных членов разложения в ряд Тейлора вектор-функции
обратной к F(X). Благодаря этому удается обеспечить такой ход итерационного процесса, при котором невязки по параметрам, не входящим в число утяжеляемых, всегда остаются в пределах допустимых значений.
Существенным преимуществом методов непрерывного утяжеления является их быстродействие и отсутствие необходимости в выборе величины шага утяжеления. Однако при этом не снимаются вычислительные сложности, связанные с вырожденностью матрицы Якоби УУР в точке решения.
для определения параметров Xпр, Yпр
В работах [30, 31, 31, 33] предложено применить уравнения предельных режимов, которые дают аналитическое описание гиперповерхности предельных режимов. Существенным свойством этих уравнений является невырожденность отвечающей им матрицы Якоби в точке решения. Этим снимаются трудности с решением плохо обусловленных СЛУ.
Параметры Xпр, Yпр. предельного по устойчивости режима могут быть найдены из решения системы нелинейных уравнений, которую можно представить в двух формах [34, 35]:
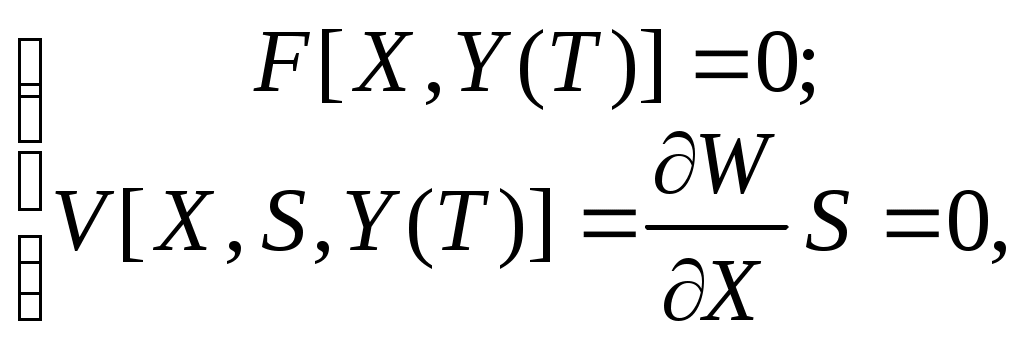(13)
или
(14)
где Y(T)=Yo+T*Y – вектор регулируемых параметров, являющийся линейной функцией скалярной переменной Т;
S=[S1 S2 … Si … Sm]T – собственный вектор матрицы
, отвечающий нулевому собственному значению ;
R – собственный вектор транспонированной матрицы, также отвечающий =0.
Уравнения (13) или (14), называемые уравнениями предельных режимов (УПР), получены на основе замены детерминатного равенства
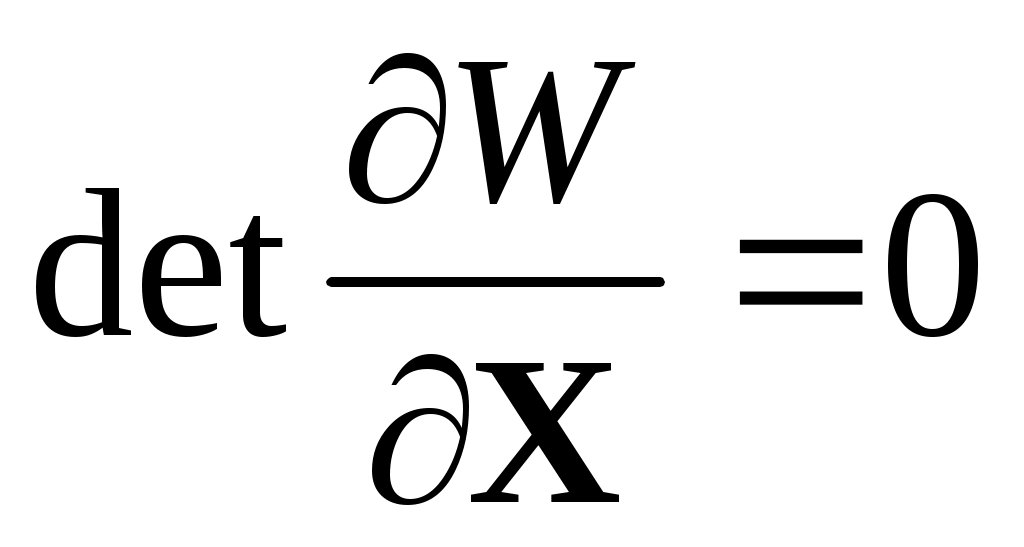
эквивалентными, аналитически представимыми соотношениями
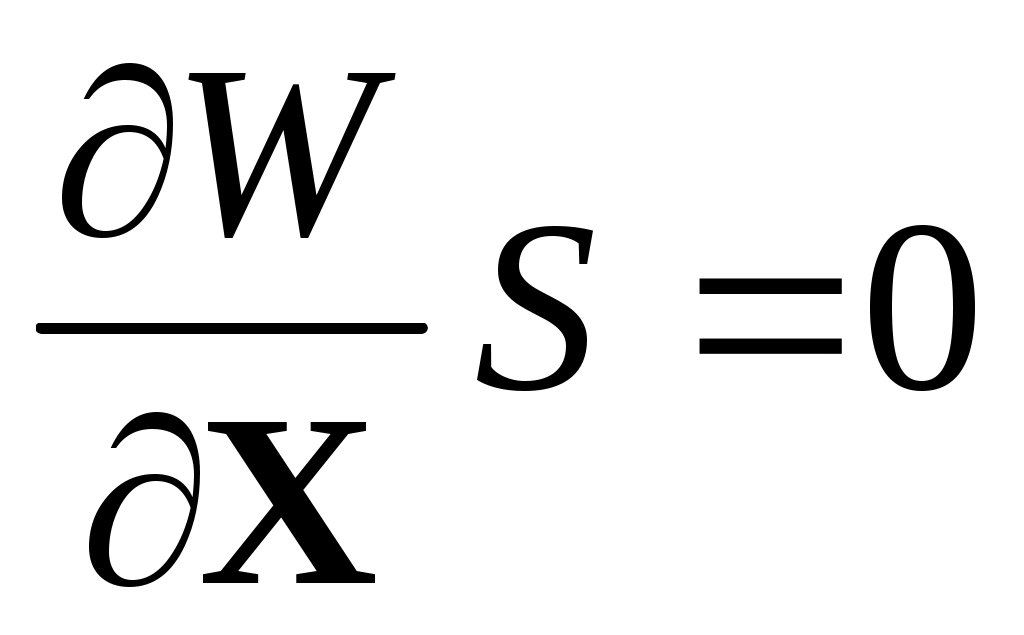или 
(15)
Решение УПР каким-либо итерационным методом позволяет определить предельный по устойчивости режим в заданном направлении утяжеления. При этом снимаются трудности, связанные с необходимостью расчета серии промежуточных режимов.
В работе [34] доказано, что при совпадении пределов передаваемой мощности и устойчивости, те есть в предположении, что
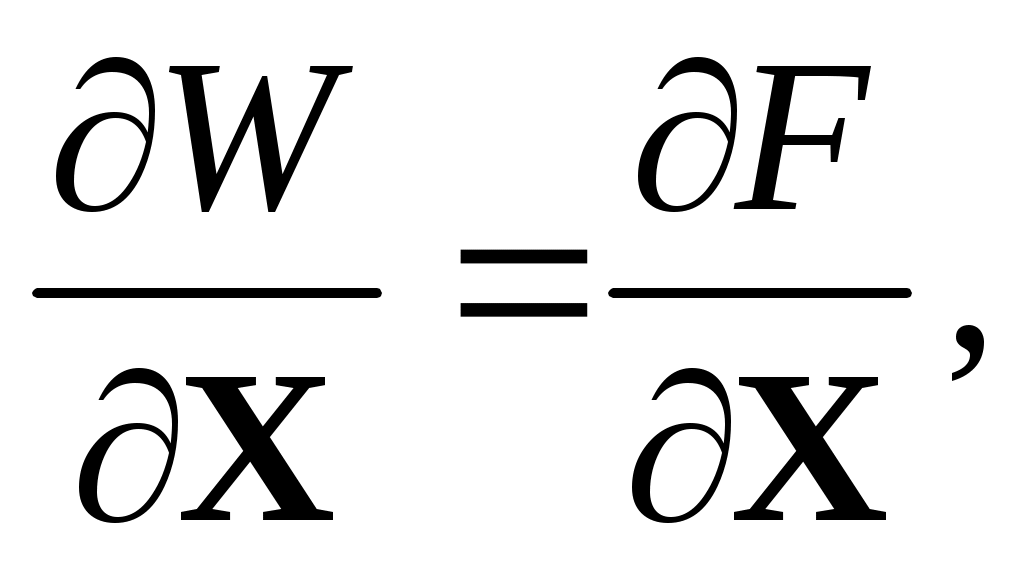
матрица Якоби УПР
или 
не вырождена в точках решения Хпр. Поэтому снимаются и трудности, связанные с решением плохо обусловленных систем линейных уравнений.
Кроме того, метод определения параметров Xпр, Yпр, основанный на использовании УПР, в отличие от методов непрерывного утяжеления, применим как при совпадении пределов устойчивости, так и при их отличии.
Из-за введения дополнительных переменных S (R) размерность УПР по сравнению с уравнениями установившегося режима повышена. Однако, как показано в работе [36], указанные переменные имеют определенный физический смысл и позволяют получить дополнительную информацию о характеристиках предельного режима.
2.4. Построение областей устойчивости
На основе соотношений (15) может быть реализована методика определения параметров Xпр, Yпр [37, 38], применимая для построения границ областей устойчивости, а также для выбора начальных приближений при определении запасов устойчивости.
Суть методики заключается в непосредственном использовании соотношений
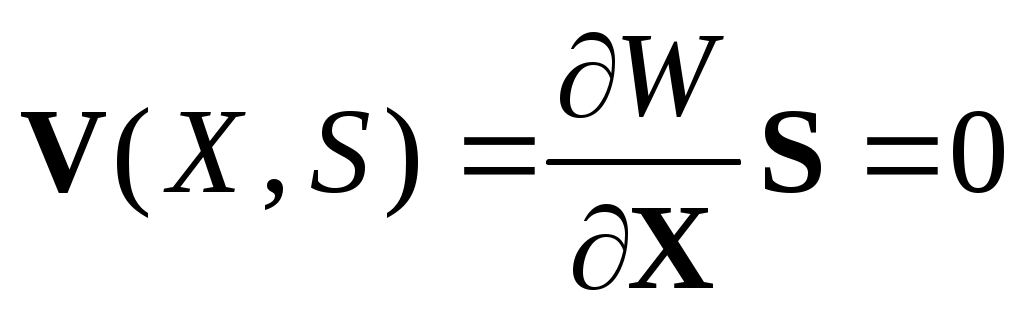(16)
или
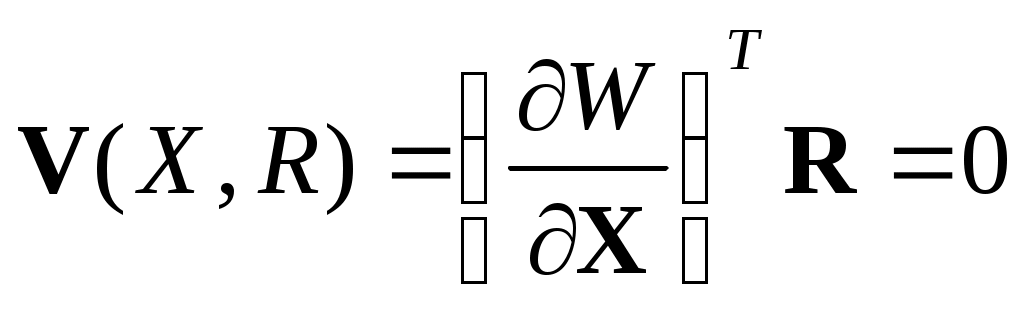(17)
для определения точек Хпр, принадлежащих поверхности LW.
Рассмотрим, в качестве примера, систему (16). Задавшись вектором S=S1 из решения уравнений
V (X, S1) = 0
можно найти соответствующие значения Хпр(1). Поворот S в положение S2 обеспечивает определение следующей точки Хпр(2) (рис. 4).
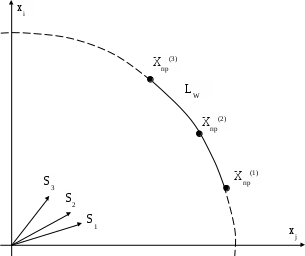
Рис. 4. К определению LW.
Таким образом, путем вращения S можно «обойти» всю предельную поверхность. Аналогично можно использовать систему (17).
По найденным значениям Хпр из УУР можно найти соответствующие значения параметров Yпр и построить границу LW в координатах Y.
ЗАКЛЮЧЕНИЕ
Все более актуальными становятся задачи, связанные с расчетом предельных режимов и оценкой запасов СУ непосредственно в цикле оперативного управления ЭС. Это приводит к необходимости разработки эффективных методов и алгоритмов, обеспечивающих как высокое быстродействие, так и надежность получения результата.
При оперативном управлении расчеты предельных режимов должны проводится в темпе процесса изменения схемно-режимной ситуации, а адекватная работа централизованных систем противоаварийной автоматики требует просмотра большого количества аварийных ситуаций за весьма короткое время, обусловленное значительной скоростью изменения параметров режима. Поэтому требуется разработка новых подходов, более полно учитывающих специфику задач оперативного управления.
На основе рассмотренного в данной работе материала существующие методы расчетов предельных по статической устойчивости режимов энергосистем можно отразить схематично на рис. 5.
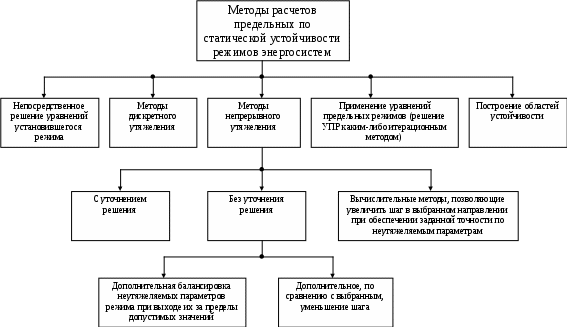
Рис. 5. Методы расчета предельных режимов
Библиографический список
, итерационная процедура (11) обеспечивает сходимость вычислительного процесса для любых существующих режимов вплоть до предельных, а при расчете несуществующих режимов процесс вычислений сходится к точке предельной гиперповерхности, где Якобиан системы УРР (предполагается, что пределы передаваемой мощности и устойчивости равны, т.е. вектор-функции F(X,Y) и W(X,Y) совпадают) равен нулю.Суть способа непрерывного утяжеления можно пояснить на ходе итерационного процесса на плоскости двух параметров Y1 и Y2. При этом исходному режиму соответствует точка (Y1(0), Y2(0)), а утяжеление осуществляется изменением параметра Y2, то есть
Начальная величина параметра Т выбирается таким образом, чтобы выйти за пределы области устойчивости (существования рушения). После первой итерации происходит переход в точку, где вследствие неучета нелинейных членов разложения функции F(X,Y) в ряд Тейлора, кроме невязок по утяжеляемому параметру (Y2(н)-Y2(1)) появляется невязка по другой координате (Y1(1)-Y1(0)). По этой причине на второй итерации направление утяжеления изменяется, осуществляется переход в точку, где также имеет место отклонение от выбранной траектории Y(T), изменение направления утяжеления и т.д. При достижении предельной поверхности LF (LW) из-за наличия результирующих невязок по параметру Y1, не являющемуся утяжеляемым, возникает несоответствие между полученной точкой и искомой точкой. Поэтому появляется необходимость в уточнении решения. При этом вычислительный процесс, на каждой итерации которого невязка по утяжеляемому параметру полагается нулевой, проходит вблизи предельной поверхности, где матрица плохо обусловлена.
Можно обойтись без процесса уточнения одним из следующих способов.
Первый из них основан на дополнительной балансировке неутяжеляемых параметров режима при выходе их за пределы допустимых значений.
Другой способ связан с дополнительным, по сравнению с выбранным (11) , уменьшением шага. Этим обеспечивается требуемая степень соответствия результирующей точки вычислительного процесса и искомой предельной точки.
Однако, обе рассмотренные модификации приводят к нежелательному увеличению количества итераций. Общей причиной указанных осложнений является линеаризация УУР при использовании итерационной процедуры (11). Указанный недостаток можно устранить с помощью применения вычислительных методов [14, 29], которые позволяют увеличить шаг в выбранном направлении при обеспечении заданной точности по неутяжеляемым параметрам.
Они основаны на дополнительном учете нелинейных членов разложения в ряд Тейлора вектор-функции
обратной к F(X). Благодаря этому удается обеспечить такой ход итерационного процесса, при котором невязки по параметрам, не входящим в число утяжеляемых, всегда остаются в пределах допустимых значений.
Существенным преимуществом методов непрерывного утяжеления является их быстродействие и отсутствие необходимости в выборе величины шага утяжеления. Однако при этом не снимаются вычислительные сложности, связанные с вырожденностью матрицы Якоби УУР в точке решения.
-
Применение уравнений предельных режимов
для определения параметров Xпр, Yпр
В работах [30, 31, 31, 33] предложено применить уравнения предельных режимов, которые дают аналитическое описание гиперповерхности предельных режимов. Существенным свойством этих уравнений является невырожденность отвечающей им матрицы Якоби в точке решения. Этим снимаются трудности с решением плохо обусловленных СЛУ.
Параметры Xпр, Yпр. предельного по устойчивости режима могут быть найдены из решения системы нелинейных уравнений, которую можно представить в двух формах [34, 35]:
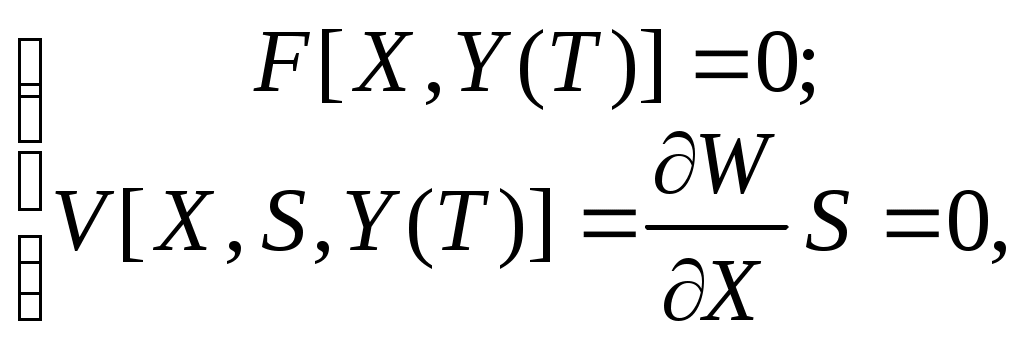(13)или
(14)где Y(T)=Yo+T*Y – вектор регулируемых параметров, являющийся линейной функцией скалярной переменной Т;
S=[S1 S2 … Si … Sm]T – собственный вектор матрицы
, отвечающий нулевому собственному значению ;R – собственный вектор транспонированной матрицы, также отвечающий =0.
Уравнения (13) или (14), называемые уравнениями предельных режимов (УПР), получены на основе замены детерминатного равенства
эквивалентными, аналитически представимыми соотношениями
или (15)Решение УПР каким-либо итерационным методом позволяет определить предельный по устойчивости режим в заданном направлении утяжеления. При этом снимаются трудности, связанные с необходимостью расчета серии промежуточных режимов.
В работе [34] доказано, что при совпадении пределов передаваемой мощности и устойчивости, те есть в предположении, что
матрица Якоби УПР
или не вырождена в точках решения Хпр. Поэтому снимаются и трудности, связанные с решением плохо обусловленных систем линейных уравнений.
Кроме того, метод определения параметров Xпр, Yпр, основанный на использовании УПР, в отличие от методов непрерывного утяжеления, применим как при совпадении пределов устойчивости, так и при их отличии.
Из-за введения дополнительных переменных S (R) размерность УПР по сравнению с уравнениями установившегося режима повышена. Однако, как показано в работе [36], указанные переменные имеют определенный физический смысл и позволяют получить дополнительную информацию о характеристиках предельного режима.
2.4. Построение областей устойчивости
На основе соотношений (15) может быть реализована методика определения параметров Xпр, Yпр [37, 38], применимая для построения границ областей устойчивости, а также для выбора начальных приближений при определении запасов устойчивости.
Суть методики заключается в непосредственном использовании соотношений
(16)или
(17)для определения точек Хпр, принадлежащих поверхности LW.
Рассмотрим, в качестве примера, систему (16). Задавшись вектором S=S1 из решения уравнений
V (X, S1) = 0
можно найти соответствующие значения Хпр(1). Поворот S в положение S2 обеспечивает определение следующей точки Хпр(2) (рис. 4).
Рис. 4. К определению LW.
Таким образом, путем вращения S можно «обойти» всю предельную поверхность. Аналогично можно использовать систему (17).
По найденным значениям Хпр из УУР можно найти соответствующие значения параметров Yпр и построить границу LW в координатах Y.
ЗАКЛЮЧЕНИЕ
Все более актуальными становятся задачи, связанные с расчетом предельных режимов и оценкой запасов СУ непосредственно в цикле оперативного управления ЭС. Это приводит к необходимости разработки эффективных методов и алгоритмов, обеспечивающих как высокое быстродействие, так и надежность получения результата.
При оперативном управлении расчеты предельных режимов должны проводится в темпе процесса изменения схемно-режимной ситуации, а адекватная работа централизованных систем противоаварийной автоматики требует просмотра большого количества аварийных ситуаций за весьма короткое время, обусловленное значительной скоростью изменения параметров режима. Поэтому требуется разработка новых подходов, более полно учитывающих специфику задач оперативного управления.
На основе рассмотренного в данной работе материала существующие методы расчетов предельных по статической устойчивости режимов энергосистем можно отразить схематично на рис. 5.
Рис. 5. Методы расчета предельных режимов
Библиографический список
-
Идельчик В.И. Расчеты и оптимизация режимов электрических сетей и систем. – М.: Энергоатомиздат, 1988. -
Идельчик В.И. Расчеты установившихся режимов электрических систем. – М.: Энегрия, 1977. -
Применение цифровых вычислительных машин в электроэнергетике /О.В. Щербачев, А.И. Зейлигер, К.П. Кадомская и др.; под ред. О.В. Щербачева/. – Л.: Энегрия, 1980. -
Жуков П.А., Стратин И.П. Установившиеся режимы сложных электрических сетей и систем: Методы расчетов. – М.: Энегрия, 1979. -
Гамм А.З. Методы расчета нормальных режимов электро-энергетических систем на ЭВМ. – Иркутск: Изд-во ИПИ, 1972. -
Баринов В.А., Совалов С .А. Режимы энергосистем: Методы анализа и управления. – М.: Энергоатомиздат, 1990. -
Фазилов Х.Ф. Методы режимных расчетов электрических систем. – Ташкент: Наука, 1964. -
Качанова Н.А. Электрический расчет сложных энергосистем на ЦВМ. – Киев: Наукова думка, 1966. -
Липес А.В., Окуловский С.К. Расчеты установившихся режимов электрических систем на ЭВМ. – Свердловск, УПИ, 1986. -
Конторович А.М., Шелухин Н.Н. Расчет режимов энергосистем при больших небалансах мощности и изменения частоты//Электричество. – 1982. - №7. -
Крюков А.В., Макаров Ю.В. Методы экспресс-расчетов установившихъся режимов электрических систем: Учебное пособие. – Улан-Удэ, Вост.-Сиб. технол. ин-т, 1990. -
Гончуков В.В., Горнштейн В.М., Крумм Л.А. и др Автоматизация управления энергообьединениями // М: Энергия. -
Идельчик В.И. Расчеты установившихся режимов// М: Энергия, 1977. -
Конторович А.М., Дунаева Н.П. Исследование методов расчета установившихся режимов, основанных на разложении решения в ряд Тейлора // Иркутск, 1978. -
Баринов В.А. Определение запаса статической апериодической устойчивости сложных электроэнергетических систем // Изв. АН СССР, Энергетика и транспорт, 1973, №1. -
Ножин Л.Э. Исследование статической устойчивости установившихся и самоустанавливающихся режимов электрических систем с помощью ЦВМ: Автореф. дис. ... канд.техн.наук.Л.,1970. -
Совалов С.А. Режимы единой энергосистемы. М.: Энергоиздат,1983. -
Цукерник Л.В. Основные положения анализа статической устойчивости сложных энергосистем при помощи вычислительных машин //Проблемы технической электродинамики. Киев: Наукова думка,1972.Вып.36. -
Цукерник Л.В. Учет влияния нелинейности математической модели энергосистемы при машинных методах расчета запаса ее устойчивости "в малом" // Проблемы нелинейной электротехники. Киев: Наукова думка,1984. -
Электрические системы / Под редакцией Веникова В.А. М.:Высшая школа,1982. -
Методы исследования устойчивости электрических систем и их использование // Сб. научных трудов ВНИИ Энергосетьпроект, М: Энергоатомиздат, 1985. -
Ушаков Е.И. Статическая устойчивость электрических систем // Сиб. энерг. ин-т, Новосибирск: Наука, 1988. -
Тьюарсон Р. Разряженные матрицы // М:Мир, 1977. -
Веников В.Н., Строев В.Н., Идельчик В.И., Тарасов В.И. Оценка статической устойчивости электрических систем на основе решения уравнений установившегося режима // Изв. АН СССР, Энергетика и транспорт, 1971, №5. -
Гончуков В.В., Горнштейн В.М., Крумм Л.А. и др Автоматизация управления энергообьединениями // М: Энергия, 1979. -
Веников В.А. Переходные электромеханические процессы в электрических системах. – М.: Высшая школа, 1985. -
Конторович А.М., Крюков А.В. Локализация слабых звеньев электрических систем с помощью практических критериев устойчивости. – Изв. вузов. Энергетика, 1983, №9. -
Тарасов В.И. Применение способа непрерывного утяжеления для определения предельных по апериодической устойчивости режимов электрических систем. – В кн.: Вопросы применения математических методов при управлении режимами и развитием электрических систем. Иркутск, 1975. -
Конторович А.М., Макаров Ю.В., Тараканов А.А. Совершенствование методов непрерывного утяжеления для определения предельных режимов электрических систем / Труды ЛПИ. – Л., 1982, №385. -
Конторович А.М., Крюков А.В. Определение предельных режимов способом непрерывного утяжеления // Л:ЛПИ, 1981,№ 380. -
Конторович А.М., Крюков А.В. Использование уравнений предельных режимов в задачах управления ЭЭС // Изв. АН СССР, Энергетика и транспорт, 1987, №3, с.25-33. -
Конторович А.М., Крюков А.В. Алгоритм решения вырожденных систем транцендентных уравнений//Тез. докл. XXVII научн. конф. ВСТИ. Улан-Удэ: Вост.-Сиб. технол.ин-т, 1988. -
Конторович А.М., Крюков А.В. Математическая модель предельных режимов энергосистем // Моделирование электроэнергетических систем. Тез.докл.Всес.научн.конф. Баку,1982. -
Конторович А.М., Крюков А.В. Предельные режимы энергосистем (Основы теории и методы расчетов). – Иркутск: Иркутский университет, 1985. -
Конторович А.М., Крюков А.В. Уравнения предельных режимов и их использование для решения задач управления энергосистемами. – В кн.: Методы исследования устойчивости сложных электрических систем и их использование. – М.: Энергия, 1985. -
Конторович А.М., Крюков А.В. Выделение слабых звеньев по статической устойчивости в сложных электрических системах. – Иркутск – Улан-Удэ, 1987. Деп. в Информэнерго, №2446-эн. -
Конторович А.М. Направление исследований по методам расчета режимов / Труды ЛПИ. – Л., 1985, №406. -
Конторович А.М., Лукина М.К. Построение областей устойчивости для трехмашинной эквивалентной схемы энергосистемы. – Л., 1984. Деп. в Информэнерго, №1517эн-Д84