2. Увязка приращений координат ∆ Х и ∆Y

1. Вычисляем приращения координат ∆ Х и ∆Y по вычисленным значениям горизонтальных проложений и румбам:





Знаки приращений определяем по названию румба и номеру четверти.
















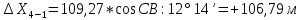
Определяем невязки и в приращениях координат по осям X и Y, пользуясь формулами: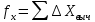





где:

, - суммы вычисленных приращений координат.

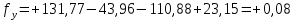м

м

Находим абсолютную линейную невязку в периметре теодолитного хода по формуле:



Определяем допустимость невязки . Для этого вычисляем относительную невязку в периметре как частное от деления невязки в периметре на периметр Р теодолитного хода и сравниваем ее с допусти­мой относительной невязкой, составляющей

---

доли периметра. Относительную невязку в периметре представляют в виде дроби, в числителе которой единица.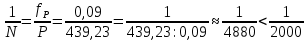



Поскольку относительная невязка допустима, то увязываем вычисленные приращения, вводя в них поправки. Поправки имеют знак, обратный знакам невязок , и распределяются пропорционально длинам сторон по формулам:



где: - поправки в приращения координат соответственно по оси Х и Y, найденные для i-й стороны;

Р - периметр полигона;

- длина i-й стороны.

Сумма поправок должна рав­няться невязке с обратным знаком.









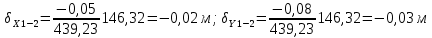
Складывая алгебраически величины вычисленных приращений с их поправками, находим исправленные приращения:

















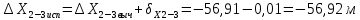
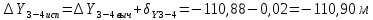
Вычисляем координаты вершин основного замкнутого хода по формулам:





где:

---

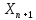
, - соответственно абсцисса и ордината последующей вершины теодолитного хода;

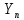, - соответственно абсцисса и ордината предыдущей вершины теодолитного хода;

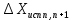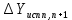, - исправленные приращения координат между предыдущей и последующей вершинами.













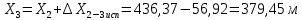
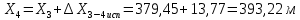
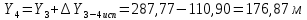
Для контроля вычисляем через координаты точки 5 координаты исходной точки:





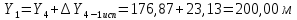
Ведомость вычисления координат замкнутого теодолитного хода

№ вершин полигона	Внутренние углы				Дирекционные углы				Румбы сторон						Длина горизонталь-ного проложения, м		Приращения																	Координаты
	измеренные		исправленные														вычисленные								исправленные
	◦	'	◦	'		◦		'		наз		◦		'			±		ΔΧ		±		ΔΥ			±		ΔΧ		±		ΔΥ			±		ΔΧ		±		ΔΥ
1	76	28	76	28																-0,02				-0,03												+		500,00		+		200,00
		+0,'5				115		46		ЮВ		64		14		146,32		-		63,61		+		131,77			-		63,63		+		131,74
2	78	4.5	78	05																-0,01				-0,01												+		436,37		+		331,74
		+0,'5				217		41		ЮЗ		37		41		71,91		-		56,91		-		43,96			-		56,92		-		43,97
3	120	35,5	120	36																-0,01				-0,02												+		379,45		+		287,77
		+0,'5				277		05		СЗ		82		55		111.73		+		13,78		-		110,88			+		13,77		-		110,90
4	84	50,5	84	51																-0,01				-0,02												+		393,22		+		176,87
						12		14		СВ		12		14		109,27		+		106,79		+		23,15			+		106,78		+		23,13
1	76	28	76	28																																+		500,00		+		200,00
						115		46
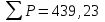																			0,05				0,08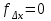

---

1. Допустимая невязка в углах

2. Абсолютная невязка в периметре

3. Относительная невязка в периметре

4. Допустимая невязка в периметре



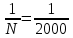
3. Определение площади полигона аналитическим способом

Площадь полигона можно вычислить по координатам его вершин. Исходными данными являются координаты станций теодолитного хода (полигона).

Двойная площадь полигона (многоугольника) равна сумме произведений абсциссы каждой точки на разность ординат последующей и предыдущей точек:



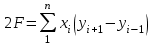
Двойная площадь полигона (многоугольника) равна сумме произведений ординаты каждой точки на разность абсцисс предыдущей и последующей точек теодолитного хода:




Вычисление площади участка по координатам

СХЕМА ПОЛИГОНА



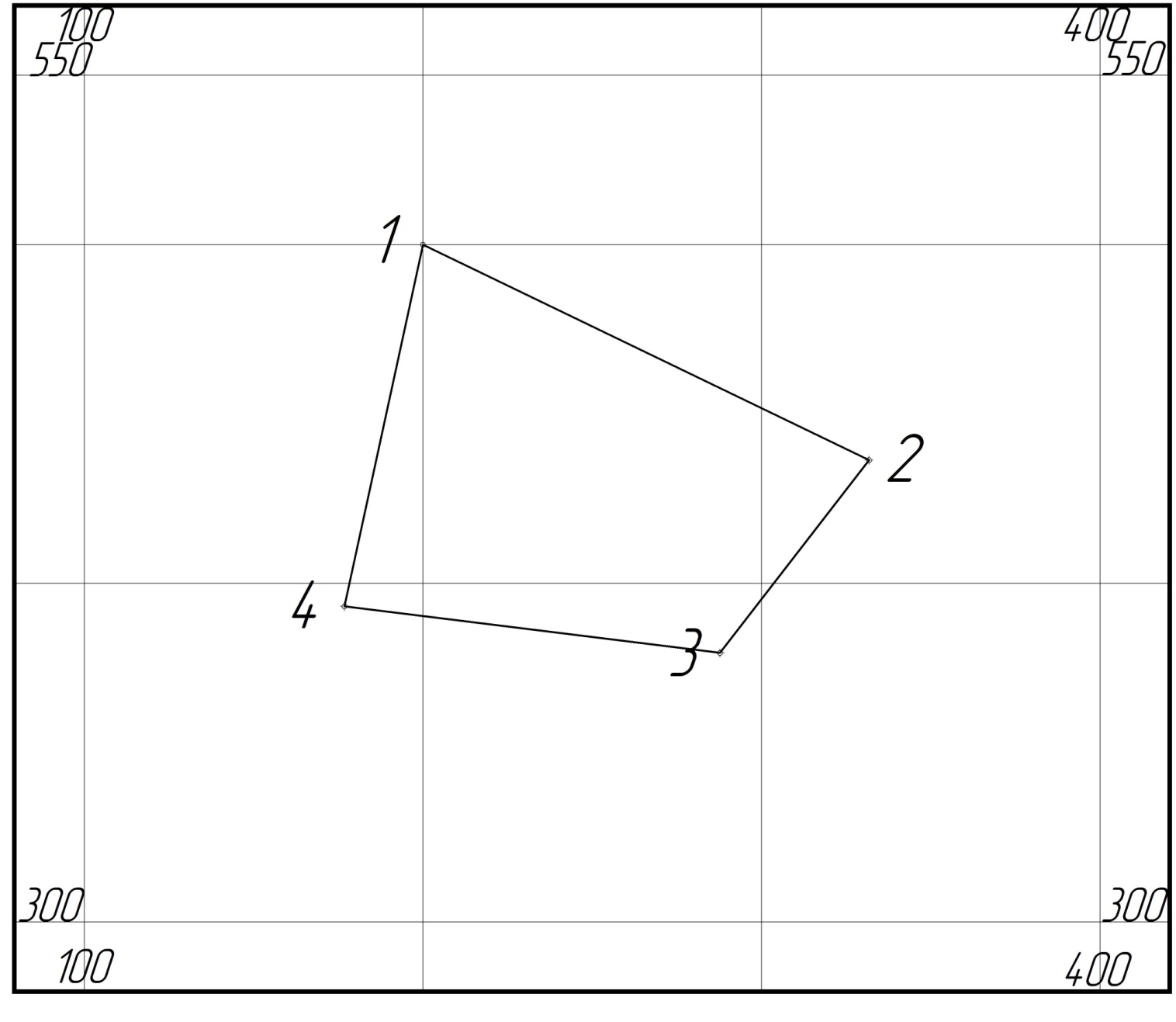
Вычисление площади полигона

№ вершин	Координаты, м
	xi	yi	xi-1 – xi+1	yi+1 – yi-1	yi (xi-1 – xi+1)	xi (yi+1 – yi-1)
1	2	3	4	5	6	7
1	500,00	200,00	-43,15	154,87	-8630,00	77435,00
2	436,37	331,74	120,55	87,77	39991,26	38300,19
3	379,45	287,77	43,15	-154,87	12417,28	-58765,42
4	393,22	176,87	-120,55	-87,77	-21321,68	-34512,92
1
Контроль			Σ = 0	Σ = 0	2F=22456,86	2F=22456,85
F = 11228,43 м2 F =1, 123 га

---

Список использованной литературы

1. 
   Инженерная геодезия / Г. В. Багратуни, В. Н. Ганьшин, Б. Б. Данилевич и др. – М.: Недра, 1984. – 344 с.
   
2. 
   Клюшин, Е.Б. Инженерная геодезия / Е.Б. Клюшин [и др.]. – М.: Academia, 2004. - 479 с.
   
3. 
   Мальцева Т.Г., Грицкив Л.Н. Учебно-методическое пособие по курсу «Инженерная геодезия» для студентов строительных специальностей и профилей всех форм обучения «Составление плана местности по результатам теодолитной съёмки». – Тольятти: ТГУ, 2010. – 38с.
   

---

Смотрите также файлы

• Б. В. Зейгарник в качестве патопсихологических примеров выделяет нарушения мышления, которые характеризуются специфической структурой. В классификации Б. В. Зейгарника можно выделить как более обобщенные группы наруш.docx

• Преподаватель Бектурова А. Е. Студент Тешебаева К. Л.pptx

• Тематическое планирование Математические ступеньки 30 часов (1 раз в неделю) занятия Тема занятия Количество часов Примечания 1 Классификация по одному признаку. 1.doc

• Определите, как Вы понимаете Ваше предназначение и призвание.docx

• Федеральное агентство связи федеральное.docx