Задача 1.

Цитата из известного произведения А.С.Пушкина «Я ПОМНЮ ЧУДНОЕ МГНОВЕНЬЕ. ПЕРЕДО МНОЙ ЯВИЛАСЬ ТЫ» была разрезана на отдельные слова, которые затем рассыпались и были составлены в произвольном порядке. Найти вероятность того, что цитата оказалась составленной правильно (знаки препинания не учитывать).

Решение:

В данной фразе 8 слов. Тогда по формуле P (A) = m/n , где m=1, так как фраза единственно возможная, а n=8 получаем P (A) = 1/8 = 0,125 = 12,5%

Ответ:

Вероятность правильного составления равна 12,5%.
Задача 2.

Вероятность сбить самолет противника выстрелом из винтовки составляет 0.004. Найти вероятность сбить самолет из 250 винтовок одновременно.

Решение:

P(A)=1-(1-0,004)^250=1-0,996^250=1-0.36714=0.6329=63,29%

Ответ:

Вероятность сбить самолет из 250 винтовок одновременно равна 63,29%
Задача 3.

Вероятность того, что студент выполняет домашние задания, равна 0.96. На экзамене такой студент получает положительную оценку с вероятностью 0.98, а студент, не делавший домашних заданий – с вероятностью 0.05. Какова вероятность события А – что студент сдаст экзамен, и вероятность события В – что он не выполнял домашние работы, если известно, что событие А произошло.

Решение:

P(B)=0.96, P(A/B)=0.98, P(A/!B)=0.05.

P(A,!B)=P(!B)P(A/!B)=P(!B/A)P(A) => P(!B/A)= P(!B)P(A/!B)/ P(A)

P(!B)=1-P(B) => P(A)=P(A/B)P(B)+P(A/!B)P(!B)=0.98*0.96+0.05*(1-0.96)=0.9408+0.05*0.04=0.9408+0.002=0.941=94.1%

P(A/!B)P(!B)/ P(A)=0.05*0.04/0.941=0.0021=0.21%

Ответ: Вероятность события, что студент сдаст экзамен, и не выполнял домашние работы 0.21%
Задача 4.

Во дворце бракосочетаний в течение одного дня было зарегистрировано шесть браков. Известно, что в течение года в среднем 10 % браков заканчиваются разводом. Найти вероятность того, что из этих пар ни одна не разведется и вероятность того, что хотя бы 2 пары разведутся.

Решение:

n=6 – кол-во семейных пар

p=0.1 - вероятность того, что отдельно взятая пара разведется

q=1-p = 1-0.1=0.9

m – кол-во разведенных пар

тогда:

а) m=0 P(m)=0.9^6=0.5314=53.14%

б) P(m≥2) = 1-(P(0)+P(1))

P(m=0) =

---

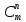
*p^m*q^n-m = 6!/(0!(6-0)!)*0.1^0*0.9^(6-0) =

720/(1*720)*1*0.5314 = 0.5314

P(m=1) = 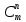*p^m*q^n-m = 6!/(1!(6-1)!)*0.1^1*0.9^(6-1) =

720/(1*120)*0.1*0.5905 = 6*0.059 = 0.3543

P(m≥2) = 1-(0.5314+0.3543) = 1-0.8857 = 0.1143 = 11.43%

Ответ:

а) Вероятность того, что из этих пар ни одна не разведется равна 53,14%

б) Вероятность того, что хотя бы 2 пары разведутся равна 11,43%
Задача 5.

Дан ряд распределения дискретной случайной величины Х:

xi	-4	-3	-1	1	3
pi	0.3	0.2	0.2	0.1	0.2

Найти математическое ожидание, дисперсию (двумя способами) и среднее квадратичное отклонение величины Х. Построить многоугольник распределения и найти вероятности pX 1, p(X 1), p1 X  3 .

Решение:

M(x) = -4*0,3+-3*0,2+-1*0,2+1*0,1+3*0,2 = -1,2+-0,6+-0,2+0,1+0,6 = -1,3

D(x) = -4^2*0.3+-3^2*0.2+-1^2*0.2+1*0.1+3^2*0.2-1.3^2 = 16*0.3+9*0.2+1*0.2+1*0.1+9*0.2-1.69 = 4.8+1.8+0.2+0.1+1.8-1.69 = 7.01

Sigma(x) = 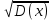= = 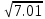2.6476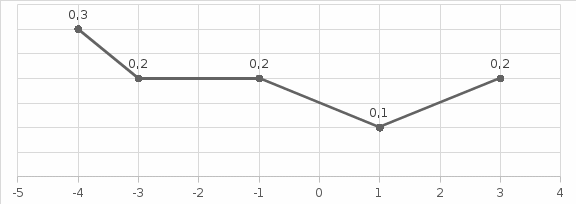



P(x<1) = P(-4)+P(-3) = 0.3+0.2 = 0.5

P(x>1) = P(3) = 0.2

P(-1
Ответ: M(x)=-1.3, D(x)=7.01, sigma(x)=2.6476
Задача 6.

Даны две дискретные случайные величины Х и У, заданные своими рядами распределения:

xi	-5	0	1
pi	0.2	0.4	0.4

yi	-1	0	3
pi	0.1	0.1	0.8

Найти законы распределения случайных величин: X², X  Y, X Y

а) Z=X²

Zi	25	0	1
Pi	0.2	0.4	0.4

б) Z=X+Y

Z₁₁=x₁+y₁=-5+-1=-6 => P(Z=-6)=0.2*0.1=0.02

---

Z₁₂=x₁+y₂=-5+0=-5 => P(Z=-5)=0.2*0.1=0.02

Z₁₃=x₁+y₃=-5+3=-2 => P(Z=-2)=0.2*0.8=0.16

Z₂₁=x₂+y₁=0+-1=-1 => P(Z=-1)=0.4*0.1=0.04

Z₂₂=x₂+y₂=0+0=0 => P(Z=0)=0.4*0.1=0.04

Z₂₃=x₂+y₃=0+3=3 => P(Z=3)=0.4*0.8=0.32

Z₃₁= x₃+ y₁₌1+-1=0 => P(Z=0)=0.4*0.1=0.04

Z₃₂=x₃+y₂=1+0=1 => P(Z=1)=0.4*0.1=0.04

Z₃₃=x₃+y₃=1+3=4 => P(Z=4)=0.4*0.8=0.32

Zi	-6	-5	-2	-1	0	1	3	4
Pi	0.02	0.02	0.16	0.04	0.08	0.04	0.32	0.32

в) Z=X*Y

Z₁₁=x₁*y₁=-5*-1=5 => P(Z=5)=0.2*0.1=0.02

Z₁₂=x₁*y₂=-5*0=0 => P(Z=0)=0.2*0.1=0.02

Z₁₃=x₁*y₃=-5*3=-15 => P(Z=-15)=0.2*0.8=0.16

Z₂₁=x₂*y₁=0*-1=0 => P(Z=0)=0.4*0.1=0.04

Z₂₂=x₂*y₂=0*0=0 => P(Z=0)=0.4*0.1=0.04

Z₂₃=x₂*y₃=0*3=0 => P(Z=0)=0.4*0.8=0.32

Z₃₁= x₃* y₁₌1*-1=-1 => P(Z=-1)=0.4*0.1=0.04

Z₃₂=x₃*y₂=1*0=0 => P(Z=0)=0.4*0.1=0.04

Z₃₃=x₃*y₃=1*3=3 => P(Z=3)=0.4*0.8=0.32

Zi	-15	-1	0	3	5
Pi	0.16	0.04	0.46	0.32	0.02

Задача 7.

Плотность распределения случайной величины Х 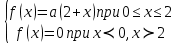. Найти нормировочную константу а, функцию распределения, математическое ожидание, дисперсию и вероятность того, что случайная величина примет значение в интервале от 0 до 1.

---

Смотрите также файлы

• Семинар по дисциплине Обществознание физическая культура студентка 3 курса гр. До911 специальность Дошкольное образование.docx

• Курсовая работа (курсовой проект) по учебному курсу Особенности проявления агрессии в среде студенческой молодежи..docx

• Дипломных проектов ф. И. О группа Руководитель проекта Тема дипломного проекта Евтеев А. А вм 983 Накрайников А. В.docx

• Что такое античность и в чём особенности возникновения и развития античной цивилизации.docx

• Автономная некоммерческая профессиональная образовательная организация Многопрофильная Академия непрерывного образования (ан поо мано) колледж зачетное задание по дисциплине Физическая культура.docx