ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.03.2024
Просмотров: 11
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ф.И.___________________________________________________________9 класс
Суммативное оценивание по геометрии за 1 четверть
ЗАДАНИЯ И СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
| Оценивание заданий работы | ||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 |
| Количество баллов | 2 | 2 | 3 | 3 | 5 | 5 |
| Всего баллов | 20 баллов | |||||
1 ВАРИАНТ
-
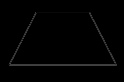
Четырехугольник ABCD – трапеция,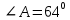
. Найдите угол между векторами
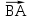и 
.
-
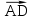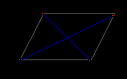
Диагонали параллелограмма PMCK пересекаются в точке О. Выразите вектор КО
через векторы
и 
.
-
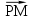Упростите выражение
-
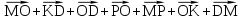
Найдите длину вектора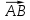
, где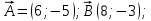 
. -
Даны вектор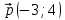
, 
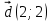и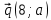 
. Найдите:
а) косинус между векторам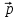и
и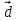 
;b) число а, если векторы
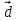и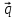 
коллинеарны;
с) число а, если векторы
и 
перпендикулярны.6. Решите задачу векторным методом. Выполните рисунок.
Дан треугольник с вершинами М (-2;8), N (6;2), K(2;-6). Найдите длину медианы МР.
Ф.И.___________________________________________________________9 класс
Суммативное оценивание по геометрии за 1 четверть
ЗАДАНИЯ И СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
2 ВАРИАНТ
| Оценивание заданий работы | ||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 |
| Количество баллов | 2 | 2 | 3 | 3 | 5 | 5 |
| Всего баллов | 20 баллов | |||||
-
Четырехугольник ABCD – ромб,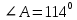
. Найдите угол между векторам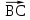и
и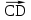 
.
-
Диагонали параллелограмма PMCK пересекаются в точке О. Выразите вектор РО
через векторы
и 
.
-
Упростите выражение
-
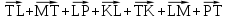
Найдите длину вектора
, где 
. -
Даны вектор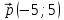
, 
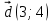и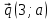 
. Найдите:
а) косинус между векторами
и 
;b) число а, если векторы
и коллинеарны;с) число а, если векторы
и перпендикулярны.6. Решите задачу. Дан параллелограмм с вершинами М (3;-4), N (-5;3), K(1;2), L (х; у). Найдите сумму координат вершины L.