Файл: Отчет Учебная практика 2 моделирование одномерного случайного блуждания методом монтекарло.docx
Добавлен: 26.03.2024
Просмотров: 12
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение высшего образования
«Адыгейский государственный университет»
Кафедра теоретической физики
Отчет
Учебная практика №2
«МОДЕЛИРОВАНИЕ ОДНОМЕРНОГО СЛУЧАЙНОГО БЛУЖДАНИЯ МЕТОДОМ МОНТЕ-КАРЛО»
Выполнила: ст. гр. 2 - Ф
Седегова В. Е.
Майкоп 2018
Содержание:
1. Введение...............................................................................................................3
2. Анализ выполненной работы.............................................................................4
3. Заключение...........................................................................................................9
4. Список литературы............................................................................................10
Введение
На кафедре (ауд. № 316) инженерно - физического факультета в период с 1806.2017 по 01.07.2017, была проведена учебная практика на тему «моделирование одномерного случайного блуждания частицы методом Монте-Карло».
Задачи практики, с точки зрения компетенций:
1) получение первичных профессиональных умений и навыков,
2) подготовка к осознанному и углубленному изучению обще-профессиональных и специальных дисциплин,
3) привитие практических профессиональных умений и навыков по избранной специальности,
4) формирование навыков самостоятельного изучения научно-технической информации,
Конкретные профессиональные задачи практики:
- Изучить основы теории вероятности, Метод Монте-Карло, на практике осуществить применение метода в конкретном случае.
Были представлены следующие задания:
Задание 1. Изучить метод Монте-Карло.
Задание 2. Применить ММК к конкретной теме.
Задание 3. Написать программу Free Pascal с применением ММК.
Анализ выполненной работы
Отчет задания № 1.
Метод Монте Карло был разработан в 1949 году, в работах Дж.Неймана, С.Улама, Н.Метрополиса. Этот метод основан на методах статистического моделирования, который был известен еще в 18 веке. В России первые статьи о методе Монте Карло были опубликованы в 1955-1956 годах.
Теоретическая основа метода была известна давно. Более того, некоторые задачи статистики рассчитывались с помощью случайных выборок, то есть фактически методом Монте Карло. Но до появления электронно-вычислительных машин, этот метод не имел широкого применения, так как моделировать случайные велечины-очень сложная работа.
В настоящее время основные усилия исследователей направлены на создание эффективных Монте Карло алгоритмов различных физических, химических и социальных процессов для параллельных вычислительных задач.
Метод Монте Карло оказал и продолжает оказывать существенное влияние на развитие методов вычислительной математики (например, развитие методов численного интегрирования) и при решении многих задач успешно сочетается с другими вычислительными методами и дополняет их.
Метод Монте Карло(ММК)- это численный метод решения математических задач при помощи моделирования случайных величин.
Суть метода заключается в следующем: процесс моделируется при помощи генератора случайных величин. Это повторяется много раз, а потом на основе полученных случайных данных вычисляются математическое ожидание и дисперсия решаемой задачи.
Случайная величина — это переменная, значения которой представляют собой исходы какого-нибудь случайного феномена или эксперимента.
Генератор случайных чисел (ГСЧ) – это алгоритм, который генерирует практически независимые друг от друга числа в последовательность.
Математическое ожидание — среднее значение случайной величины (распределение вероятностей стационарной случайной величины) при стремлении количества выборок или количества измерений (иногда говорят — количества испытаний) её к бесконечности.
Дисперсия случайной величины — мера разброса значений случайной величины относительно её математического ожидания.
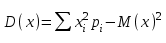
Обычный алгоритм Монте-Карло интегрирования
Предположим, требуется вычислить определённый интеграл
{\displaystyle \int \limits _{a}^{b}f(x)\,dx}
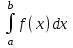
Рассмотрим случайную величину u, равномерно распределённую на отрезке интегрирования
. Тогда 
также будет случайной величиной, причём её математическое ожидание выражается как
Где
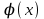- плотность распределения случайной величины u, равная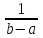 
Итак, бросаем N точек, равномерно распределённых на
. В итоге получаем оценку интеграла:
Точность оценки зависит только от количества точек N.
Отчет задания № 2.
Случайное блуждание — математическая модель процесса случайных изменений — шагов в дискретные моменты времени.
Дискретный момент времени - это момент времени, состоящий из отдельных частей, прерывный, дробный. При этом предполагается, что изменение на каждом шаге не зависит от предыдущих и от времени.
Будем рассматривать движение частицы по прямой, за 0 примем начало отсчета.
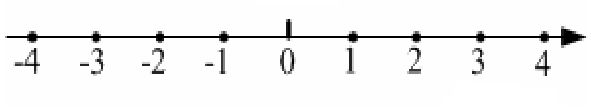
Рис1. Одномерное случайное блуждание частицы.
Частица может двигаться в право или лево от начала отсчета. Один шаг равен L Движение части в лево «л», движение частицы в право «п». Полное число движений частицы N=л+п. Тогда полное смещение частицы от начала координат после N шагов равно x=(п-л)L, где –NL
Вычислим среднее смещение M(x) и дисперсию D(x) смещения пешехода. Усреднение производится по всем возможным блужданиям, состоящим из N шагов.
Исследование задачи случайного блуждания, сформулированной выше, можно провести аналитически, воспользовавшись теорией вероятностей.
В результате для мат ожидания и дисперсии получаем аналитические выражения
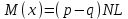
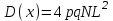
Рассматриваем симметрический случай, тогда имеем p=q=0,5. Моделирование блужданий не имеет точного решения. Два важных метода моделирования — точный комбинаторный метод (метод полного перебора) и метод Монте-Карло. В методе, основанном на полном переборе, количество и вероятность всех блужданий для заданных N и х вычисляются в явном виде. Рассмотрим 8 случайных блужданий в одномерном пространстве для N=3. Заметим, что число блужданий для положительных и отрицательных значений х одинаково.
Имеем общее движение частиц с их вероятностями:
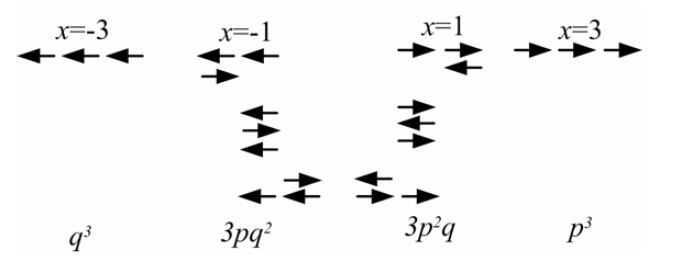
Рис.3.
Восемь случайных блужданий в одномерном (d = 1) случае при N = 3 и полном смещении х: для наглядности отдельные шаги изображены смещенными по вертикали; приведена также вероятность Р3(х), где р – вероятность шага вправо, а q = 1 – р — вероятность шага влево.
Для данного случая вычислим
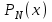. х=4, N=3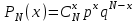
Для данного случая получим мат ожидания и дисперсию в общем виде:
Отчет задания № 3.
Блок схема
Рис2. Блок схема
Программа реализованная в Free Pascal
Program MMK;
Uses crt;
Var x1,x2, x3, x4, p, q, P1, Mx, Dx;
Begin
p:=0.5;{вероятность шага в право}
q:=1-p;{вероятность шага в лево}
If (0
Begin
P1:=0,0078125; {вероятность 8 блужданий, получена по формуле}
Randomize;{генератор случайных величин}
x1:= Random(100); WriteLn (‘x1’,x1:4:0);
x2:= Random(21); WriteLn (‘x2’,x2:4:0);
x3:= Random(125); WriteLn(‘x3’,x3:4:0);
x4:= Random(27); WriteLn(‘x4’,x4:4:0);
Mx:=x1*P1+x2*P1+x3*P1+x4*P1;{мат ожидание}
WriteLn(‘Mx’, Mx:10:3);
Dx:=x1*x1*P1+x2*x2*P1+x3*x3*P1+x4*x4*P1-Mx*Mx;{дисперсия}
WriteLn(‘Dx’, Dx:10:3); ReadLn;
End
Else WriteLn(‘p and q >0’);
End.
Заключение
По окончанию практики следует отметить, что все задания с соответствующими требованиями были выполнены. Т.е.:
- Был изучен основной теоретический, необходимый материал для выполнения задания.
- Были выполнены все основные задания, назначенные руководителем практики.
- В соответствии с требованиями, в течении прохождения практики, был введен конспект с краткими записями по вышеуказанным работам.
- Были сформированы навыки, необходимые для проведения подобных работ в будущем.
Список литературы
-
Малютин, В.М. Компьютерное моделирование физических явлений. / В.М Малютин, Е.А. Склярова-Томск: Издательство ТПУ, 2004.- 155 с. -
Ермаков, С.М. Метод Монте-Карло в вычислительной математике / С.М. Ермаков. - СПб: Невский Диалект; М.: БИНОМ. Лаборатория знаний, 2009. — 192 с.