Добавлен: 27.03.2024
Просмотров: 10
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача 2
И
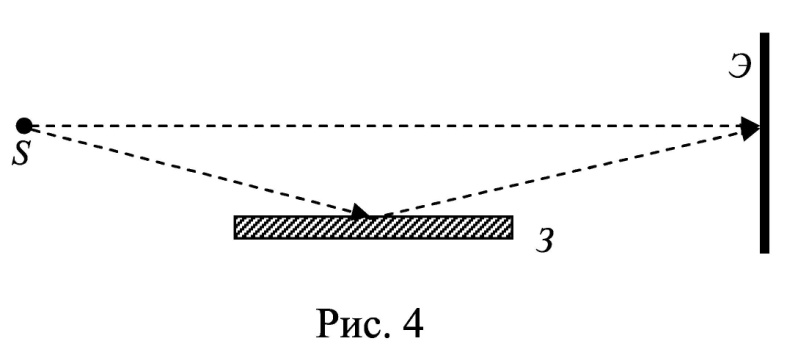нтерференционная картина на экране Э образуется при сложении световой волны, исходящей от когерентного источника Sв виде тонкой нити, и волны, отраженной от плоского зеркала З (рис. 4). Расстояние L = 1 м от источника до экрана значительно превышает расстояние от источника до плоскости зеркала. Длина волны излучения равна λ = 500 нм. Ширина интерференционных полос на экране составляет Δx= 0.25 мм. Во сколько раз увеличится ширина интерференционных полос, если источник отодвинуть от плоскости зеркала на Δh и придвинуть к плоскости экрана на ΔL?| Дано: (вар.16) L = 1 м λ = 500 нм= = 5∙10-7 м Δx= 0.25 мм = 0,25∙10-3 м Δh = 0.2 мм = 0,2∙10-3 м ΔL = 0,25 м Найти: 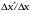 | Решение: 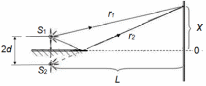 На рисунке показана интерференция в схеме Ллойда (так называется этот способ наблюдения интерференции). Источник S1 помещается вблизи от плоского зеркала. Интерферируют прямая и отражённая от зеркала световые волны, что эквивалентно появлению второго (мнимого) когерентного источника S2 на том же расстоянии от зеркала. Таким образом, мы имеем два близких когерентных источника, как и в схеме со щелями Юнга. Минимумы наблюдаются, когда оптическая разность хода волн равна полуцелому числу длин волн 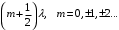 Вычислим геометрическую разность хода лучей ∆r, учитывая, что d << L (см рис.) 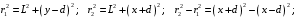 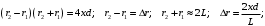 При вычислении оптической разности хода учитываем, что луч, отражённый от зеркала меняет фазу на π, что эквивалентно полуволне λ/2. Распространение лучей в воздухе (n = 1) не изменяет оптическую разность хода. Итак, получаем условие минимума при интерференции 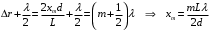 Ширина полосы определяется разностью координат двух минимумов 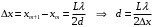 (1) Если источник отодвинуть от плоскости зеркала на Δh, то расстояние между источниками увеличится на 2Δh. Таким образом, получаем новую ширину полос 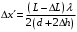 (2)Искомое отношение 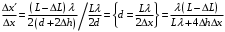 вычисляем 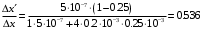 Ответ: ширина полос уменьшится в 1/0,536 = 1,87 раз. |
Задача 3
На дифракционную решетку нормально падает монохроматический свет с длиной волны λ. Угол между направлениями на дифракционные максимумы первого и второго порядков составляет Δθ. Определить период дифракционной решетки.
| Дано: (вар.16) λ = 650 нм Δθ = 150 | Решение: 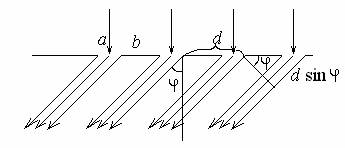 Дифракционная решётка-это периодическая совокупность прозрачных участков (щелей) и непрозрачных участков стеклянной пластины (щелевая решётка). Постоянная решётки d (период решётки) - расстояние между центрами соседних щелей. Проходя через решётку, свет разбивается на ряд пучков и, таким образом, образуются когерентные вторичные источники, излучения которых в результате интерференции усиливаются в определённых направлениях. Эти направления определяются углом φ, входящим в формулу дифракционной решётки: 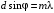 (1) d – период решётки, m– порядок максимума, λ - длина волны, φ – угол отклонения лучей, образующих максимум с данной длиной волны Записываем (1) для двух максимумов (m= 1 иm= 2) и выражаем искомую величину 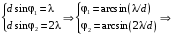 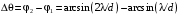 Если считать углы малыми и заменить синусы углами, погрешность будет значительной. Для точного расчёта применим формулы тригонометрии и численный метод решения уравнения. Обозначим 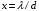 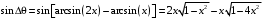 Уравнение (2) решаем численно подбором корня 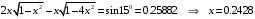 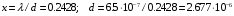 м = = 2,68 мкм проверка 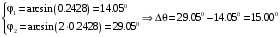 верноОтвет: постоянная решётки d= 2,68 мкм |
