Добавлен: 27.03.2024
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 |
| МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ |
| Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА - Российский технологический университет» РТУ МИРЭА |
| Институт искусственного интеллекта |
| Кафедра общей информатики |

| ОТЧЕТ ПО ПРАКТИЧЕСКОЙ РАБОТЕ № 5 построение комбинационных схем, реализующих СДНФ и СКНФ заданной логической функции от 4-х переменных | |
| по дисциплине | |
| «ИНФОРМАТИКА» | |
| Выполнил студент группы ИКБО-13-22 | Газимагомедов М.А. |
| Принял Ассистент кафедры ОИ | Павлова Е.С. |
| Практическая | «»2021 г. | _______________ |
| работа выполнена | | (подпись студента) |
| «Зачтено» | «»2021 г. | _______________ |
| | | (подпись руководителя) |
Москва 2022
СОДЕРЖАНИЕ
1Постановка задачи 3
2Проектирование и реализация 4
2.1 Восстановленная таблица истинности 4
2.2 Формулы СДНФ и СКНФ 4
2.3 Комбинационные схемы, реализующие СДНФ и СКНФ 5
3Выводы 7
4Информационный источник 8
-
Постановка задачи
Логическая функция от 4-х аргументов задана в шестнадцатеричной векторной форме. Восстановить таблицу истинности. Записать формулы СДНФ и СКНФ. Построить комбинационные схемы СДНФ и СКНФ в лабораторном комплексе. Протестировать работу схем и убедиться в их правильности.
В персональном варианте логическая функция, заданная в шестнадцатеричной форме, имеет вид F (a,b,c,d) = d9EC16.
-
Проектирование и реализация
2.1 Восстановленная таблица истинности
С помощью перевода заданной функции в двоичную запись получим столбец её значений: d9EC16 = 11011001111011002. Используем его для восстановления таблицы истинности функции (см. таблицу 1).
Таблица 1 – Таблица истинности заданной функции
| a | b | c | d | F |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 |
2.2 Формулы СДНФ и СКНФ
Запишем формулу СДНФ (1) для заданной функции, рассмотрев те наборы значений аргументов, при которых функция принимает значение 1. Каждый набор представляем в виде конъюнкции аргументов. Чтобы получить единицу в значении функции мы должны инвертировать нулевые аргументы в каждом наборе. Объединив полученные конъюнкции с помощью дизъюнкций, мы получим итоговую формулу СДНФ (1)
Запишем формулу СКНФ (2) для заданной функции, рассмотрев те наборы значений аргументов, при которых функция принимает значение 0. Каждый набор представляем в виде дизъюнкции аргументов. Чтобы получить 0 в значении функции мы должны инвертировать единичные аргументы в каждом наборе. Объединив полученные дизъюнкции с помощью конъюнкций, мы получим формулу СКНФ (2)
2.3 Комбинационные схемы, реализующие СДНФ и СКНФ
В лабораторном комплексе построим схему, реализующую СДНФ. Воспользуемся аналитической формулой (1). После построения убедимся в правильности выполненной работы. Схема представлена на рис. 1
Аналогично построим комбинационную схему для СКНФ, используя формулу (2). После построения убедимся в правильности выполненной работы. Схема представлена на рис. 2

Рисунок 1 – Схема СДНФ
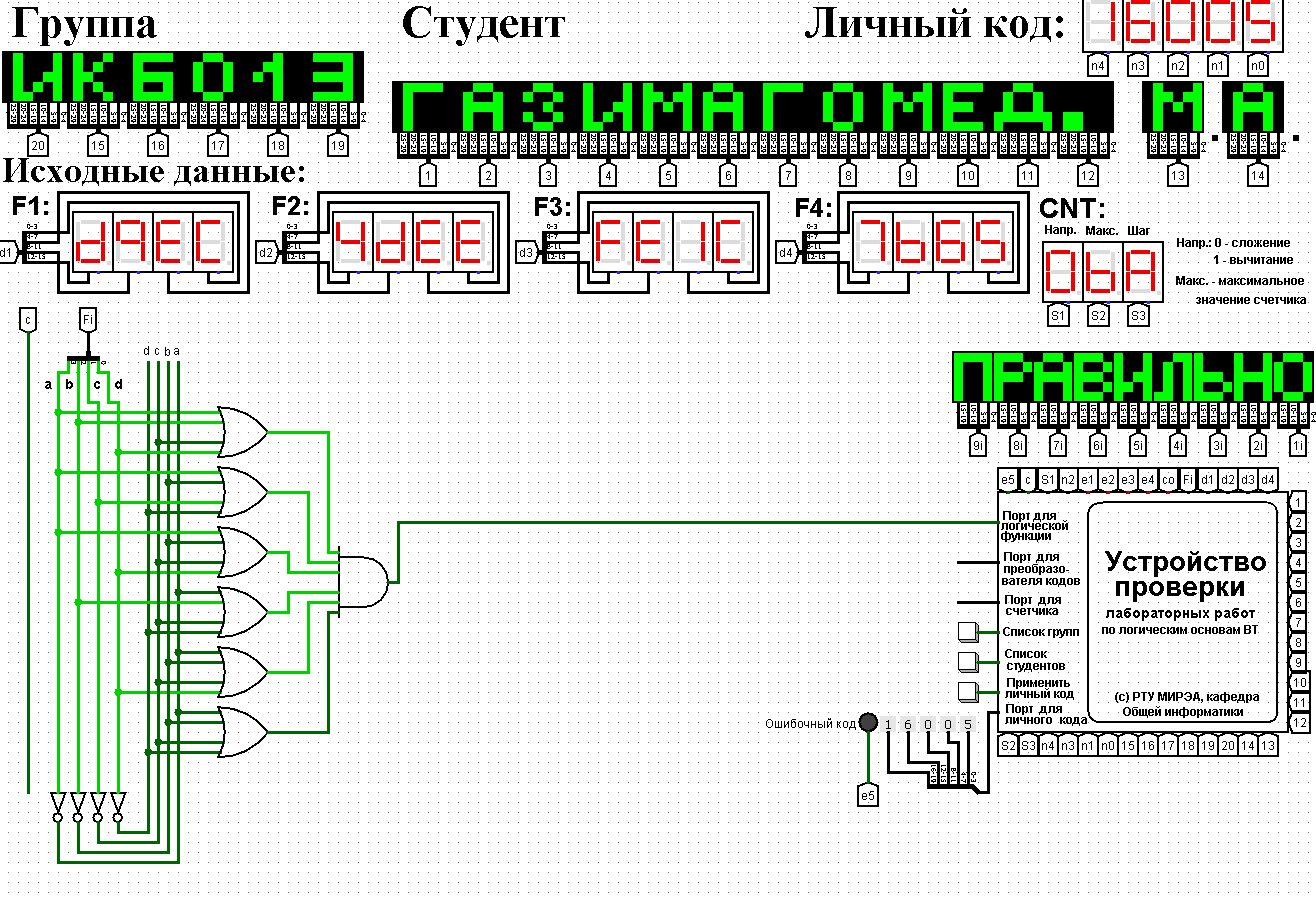
Рисунок 2 – Схема СКНФ
-
Выводы
В ходе практической работы была восстановлена таблица истинности заданной функции, из которой были выведены формулы СДНФ и СКНФ. Были построены комбинационные схемы СДНФ и СКНФ в лабораторном комплексе. С помощью среды Logisim была проверена правильность проделанной работы.
-
Информационный источник
Информатика: Методические указания по выполнению практических работ / С.С. Смирнов, Д.А. Карпов — М., МИРЭА — Российский технологический университет, 2020. – 102

