Задача № 1-18
На двух одинаковых капельках воды находятся по два лишних электрона. При этом сила электрического отталкивания капелек уравновешивает силу их взаимного тяготения. Определить радиусы капелек.
Решение
Кулоновская сила уравновешивается гравитационной
Fk=Fg
k·2·e/R²=g·2·m/R²
k=9e(+9)
g=6,67e(-11)=1.6e(-19)
массу можно рассчитать 
m=pV
p=1000
кг/м³ – плотность воды
V=(4/3)·pi()·R³

Результат
ke/g = (4/3)·pi()·R³


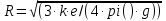
R=1.73 м
Как видим, электрическое поле намного сильнее
гравитационного.

Задача № 1-48
Найти потенциал в точке, находящейся на высоте h/2 над металлической плоскостью, в двух случаях: а) плоскость заряжена с поверхностной плотностью ; б) плоскость незаряженна, а на высоте h находится точечный заряд +e.
Решение
Потенциал точки относительно данной плоскости.
1. Напряжённость эл. поля, созданного зарядами плоскости, равна E=s/(2e₀),
где s -сигма заряда, e₀ - эпсилон нулевое.

Отсюда потенциал U1=hs/(4e₀).
2. Заменяем плоскость зеркально расположенным зарядом -e.
В такой системе потенциал всех средних точек поло жим нулевым. Потенциал исходной точки
U2=k*e[(2/h)^2-(2/(3h))^2]=(35/9)*ke/h^2 (здесь 1/k=4пe₀)

Напряженность бесконечной плоскости : Е= σ/2ε*ε₀

Задача № 2-48
Гальванический элемент даёт на внешнем сопротивлении 8 Ом ток 0,8 А, а на сопротивлении 15 Ом ток 0,5 А. Определить ток короткого замыкания.
Решение



Задача № 1-78
Плоский конденсатор заряжен до 120 В. Определить диэлектрическую проницаемость изолирующего слоя, если площадь одной пластины 60 см

---

², заряд на ней 10^8 Кл, а расстояние между пластинами 6 мм. Определить также силу взаимодействия пластин.
Решение
1. Диэлектрическую проницаемость ε найти можно из формул электроемкости плоского конденсатора

C=qU=ε⋅ε0⋅Sd

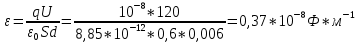2. Силу взаимодействия пластин можно найти как взаимодействие заряда q одной пластины, которая находится в электрическом поле второй пластины (учтем, что напряженность одной пластины конденсатора в 2 раза меньше напряженности между пластинами), т.е.

F=q⋅E=q⋅U2d.



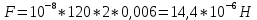
Задача № 2-98
Две электроплитки соединены параллельно и потребляют мощность N. Какую мощность они будут потреблять, включённые последовательно, если одна из них потребляет мощность N₁?
Решение
Уравнения мощностей: N1, N2:
N1=U^2/R1;

N2=U^2/R2;

Отсюда мощность при последовательном соединении:
N3=U^2/(R1+R2) --> 1/N3=R1/U^2+R2/U^2,
1/N3=1/N1+1/N2=1/N1+1/(N-N1);
N3=N1(1-N1/N)


Задача № 3-18
Ток силой 25 А течет по длинному прямому проводу, согнутому под углом 60⁰. Определить напряженность магнитного поля в точке А, находящейся на биссектрисе угла на расстоянии а=60 см от его вершины.





Решение




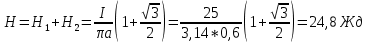
Задача № 3-48
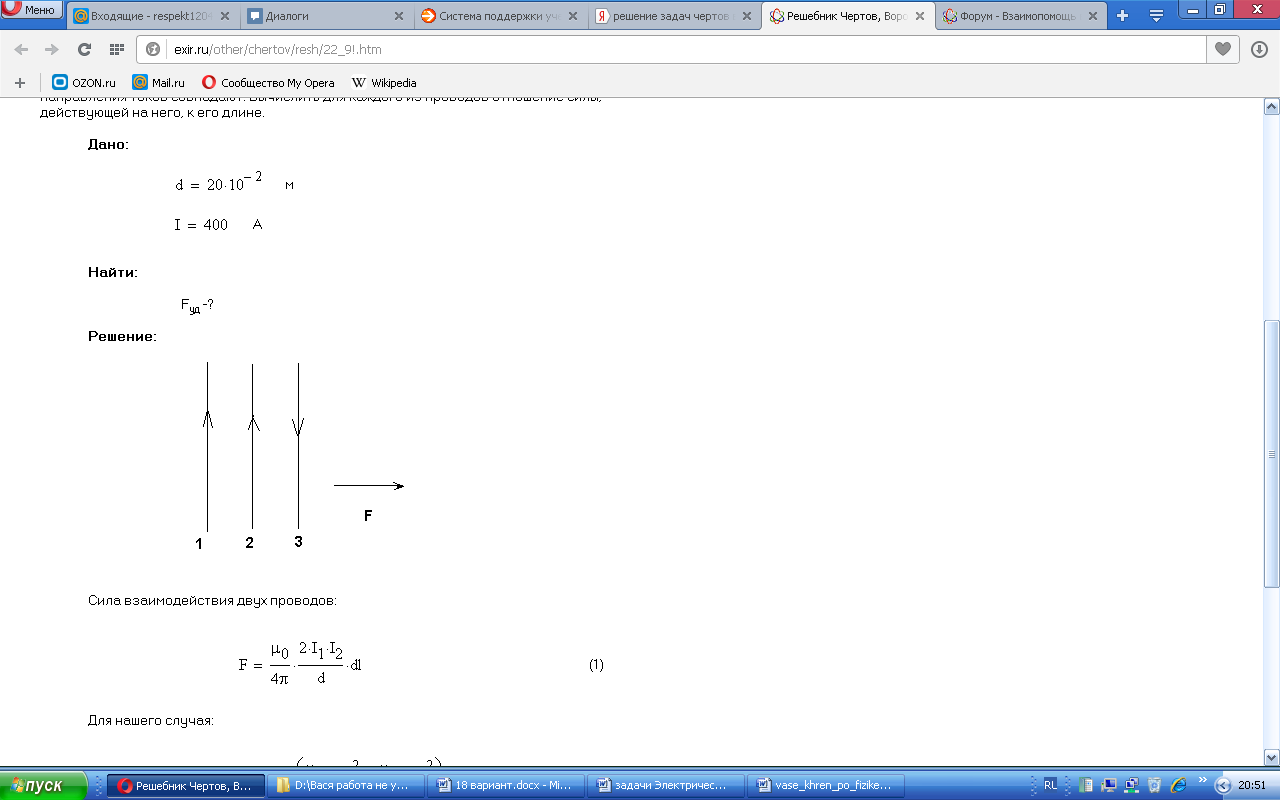
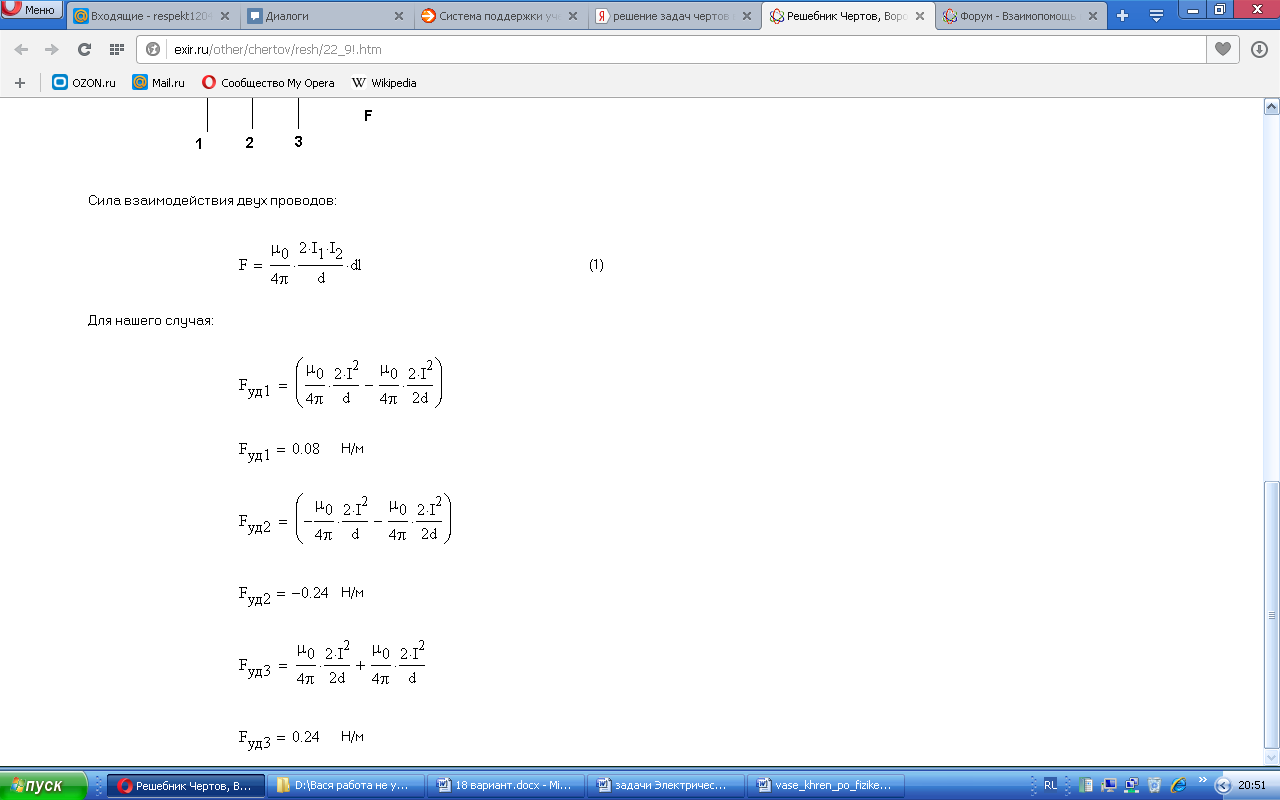
По трем прямым параллельным проводникам, находящихся на одинаковом расстоянии в 8 см друг от друга, текут токи по 10 А. При этом по двум проводникам токи текут в одном направлении. Вычислить силу, действующую на единицу длины каждого проводника.
Решение

---

Задача № 6-18
Соленоид содержит N = 800 витков. При силе тока I = 1 А магнитный поток Ф = 0,1 мВб. Определить энергию W магнитного поля соленоида. Сердечник выполнен из немагнитного материала. Магнитное поле во всем объеме однородно.
Решение



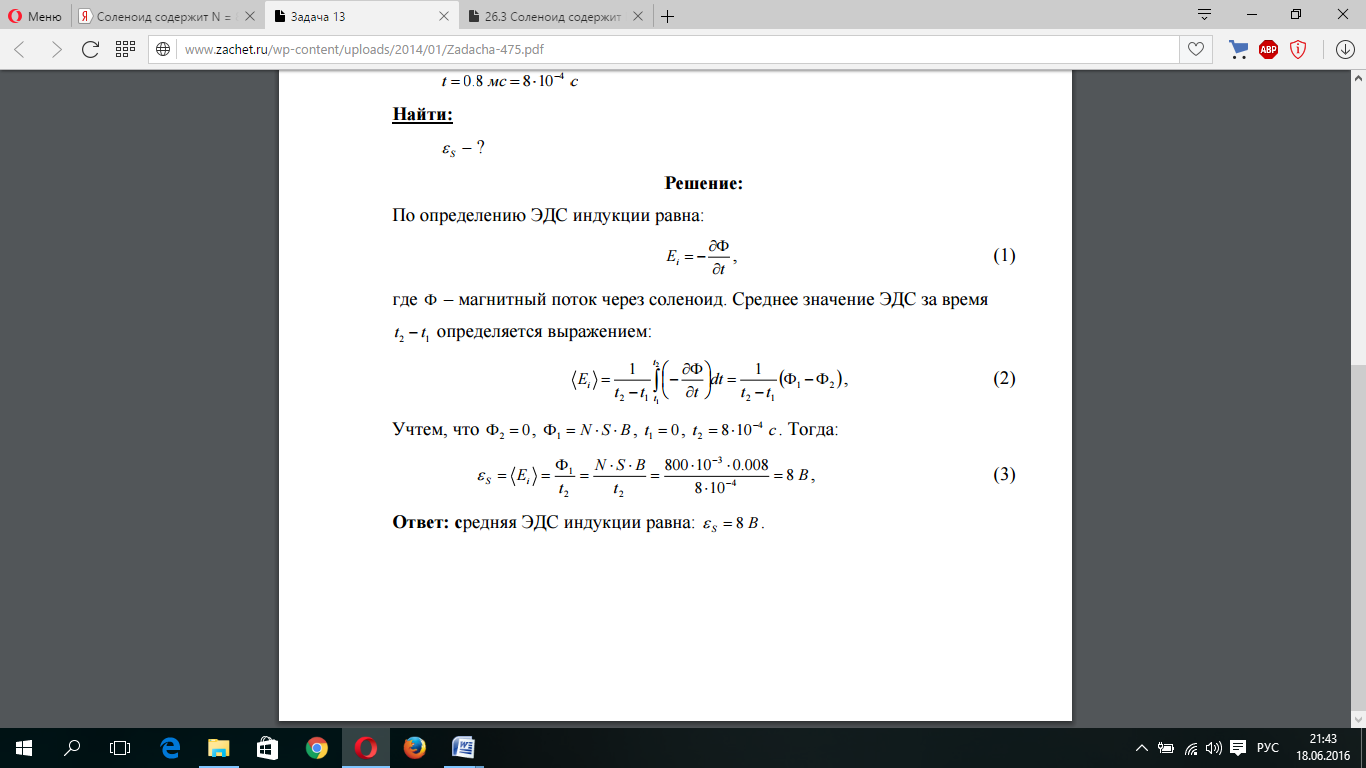
Задача № 5-18
Виток радиусом 5 см расположен перпендикулярно магнитному полю напряженности 5·10⁵ А/м. Определить сопротивление витка, если при исчезновении поля через виток проходит заряд 1 мКл.
Решение
∆Ф=∆B*Scosa-поток вектора магнитной индукции 

ε=-∆Ф/∆t

ε*∆t=-∆Ф

ε*∆t=∆B*Scosa

cos a=1 

S=pi*r^2

∆B=B

ε=IR

IR∆t=B*S

Q=I∆t

QR=B*S

R=B* pi*r^2/Q

R=0,1*pi*0,02^2 / 0,001= 0,125664 Ом = 0,126 Ом

Ответ 0,126 Ом

Задача № 4-18
Спираль, по которой движется протон в однородном магнитном поле индукции B, имеет диаметр d и шаг h. Определить скорость протона.
Решение
раз движется по спирали значит скорость направлена под непрямым углом к вектору магнитной индукции записываете формулы
радиус спирали r = (m*v*sin fi)/(e*B)
шаг спирали h = (2*pi*m*v*cos fi)/(e*B)
делим первое на второе
r/h = tg fi / (2*pi)
fi = arctg 2*pi*r/h
теперь из формулы для радиуса
v = r*e*B/(m*sin(arctg 2*pi*r/h)) = d*e*B/(2*m*sin(arctg pi*d/h))

---

Смотрите также файлы

• 5ВерноБаллов 1,00 из1,00Тест начат Четверг, 26 января 2023, Состояние.pdf

• Исходные данные Основные средства 696 000.docx

• Контрольные вопросы к разделу Вводные сведения об информационных технологиях.docx

• Практическая работа 2 Выполнил(а) Сикорская Елена Юрьевна Преподаватель Хромых Александр Владимирович.pdf

• А. А. Леонтьев Функционально грамотный человек это человек.docx