Файл: Лабораторная работа 1 дисциплина Информационные технологии в сфере транспортного бизнеса и логистики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Дальневосточный государственный университет путей сообщения»
Кафедра «Технология транспортных процессов и логистика»
Лабораторная работа №1
дисциплина «Информационные технологии в сфере транспортного бизнеса и логистики»
ЛР 23.05.04.19.01.
Студент_________________________________________
(подпись, дата)
Руководитель ___________________________________
(подпись, дата)
Хабаровск 2022
Для данного типа самолета известны: предельная коммерческая загрузка Q и полезный объем V в условных единицах. Самолет должен одним рейсом (с промежуточными посадками) обслужить 5 пунктов маршрута и возвратиться в исходный пункт, получив при этом максимальную прибыль. Матрица стоимости перелета из пункта в пункт приведена в таблице 1, вследствие различных скидок она не симметричная.
Требуется: определить оптимальный вариант загрузки самолета и маршрут перевозки коммерческого груза приносящих максимальный выигрыш.
Исходные данные:
| n1 | n2 | n3 | n4 | n5 |
| 0 | 0 | 8 | 3 | 6 |
Таблица 1
Матрица стоимости перелета
| узлы\ пункты | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | - | 25 | 45 | 15 | 30 | 33 |
| 2 | 5 | - | 15 | 1 | 30 | 33 |
| 3 | 28 | 23 | - | 43 | 13 | 6 |
| 4 | 23 | 18 | 28 | - | 23 | 23 |
| 5 | 16 | 51 | 31 | 56 | - | 11 |
| 6 | 28 | 8 | 8 | 16 | 11 | - |
Рейсом может быть перевезено два груза: один более дорогой, но тяжелый, второй полегче, но дешевый. Стоимость единицы веса груза первого вида составляет S1, второго S2.
Отношение удельных объемов грузов:
 , (1)
, (1)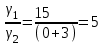 .
.Отношение полезного объема к
 :
: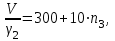 (2)
(2)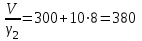 .
.Предельная коммерческая загрузка Q равна:
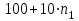 , (3)
, (3) .
.Соответственно:
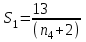 , (4)
, (4) ,
,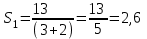
Решение:
Определим верхнюю границу маршрута ZВ(T):

Следовательно, стоимость оптимального маршрута
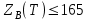 .
.Найдем нижнюю границу всего маршрута Н.
Произведем редукцию строк и столбцов матрицы.
Новая оптимизированная матрица стоимости перелета приведена в таблице 2.
Таблица 2
| узлы\ пункты | 1 | 2 | 3 | 4 | 5 | 6 | Ci |
| 1 | - | 10 | 22 | 0 | 10 | 18 | 15 |
| 2 | 0 | - | 6 | 0 | 24 | 32 | 1 |
| 3 | 18 | 17 | - | 37 | 2 | 0 | 6 |
| 4 | 1 | 0 | 2 | - | 0 | 5 | 18 |
| 5 | 1 | 40 | 12 | 45 | - | 0 | 11 |
| 6 | 24 | 8 | 0 | 16 | 6 | - | 0 |
| Сj | 4 | 0 | 8 | 0 | 5 | 0 | 68 |
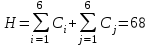 , (5)
, (5)В таблице 2 в строках и столбцах есть по несколько элементов с Сij = 0, поэтому необходим, рассмотреть варианты и сделать выбор, какое первое звено включить в маршрут. Выбирается то звено, которое имеет минимальную стоимость и максимальное значение штрафа Фij.
 , (6)
, (6)где
 - кроме опорного,
- кроме опорного,  - кроме опорного.
- кроме опорного.Таблица 3
| узлы\ пункты | 1 | 2 | 3 | 4 | 5 | 6 | Ci | Ai |
| 1 | - | 10 | 22 | 0 | 10 | 18 | 15 | 10 |
| 2 | 0 | - | 6 | 0 | 24 | 32 | 1 | 0 |
| 3 | 18 | 17 | - | 37 | 2 | 0 | 6 | 4 |
| 4 | 1 | 0 | 2 | - | 0 | 5 | 18 | 1 |
| 5 | 1 | 40 | 12 | 45 | - | 0 | 11 | 1 |
| 6 | 24 | 8 | 0 | 16 | 6 | - | 0 | 0 |
| Сj | 4 | 0 | 8 | 0 | 5 | 0 | 68 | |
| Вj | 1 | 0 | 10 | 0 | 2 | 0 | | |
| звено | 1,4 | 2,1 | 2,4 | 3,6 | 4,2 | 5,6 | 6,2 | 6,3 | 6,5 |
| Фij | 10 | 1 | 0 | 4 | 1 | 1 | 0 | 10 | 2 |
Таким образом, в качестве опорного звена выбираем (1,4).
Определим нижнюю границу стоимости.
Мы выяснили, что на первом шаге решения выгоднее всего взять звено (1,4). Но мы можем его и не брать, предполагая, что в дальнейшем это даст больший выигрыш. Если в маршруты мы не включаем звено (1,4) , то нижней границей будет:
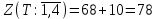 .
.Новая матрица стоимостей:
Таблица 4
| узлы\ пункты | 1 | 2 | 3 | 5 | 6 |
| 2 | 0 | - | 14 | 26 | 32 |
| 3 | 18 | 17 | - | 4 | 0 |
| 4 | 1 | 0 | 10 | 2 | 5 |
| 5 | 1 | 40 | 20 | - | 0 |
| 6 | 16 | 0 | 0 | 0 | - |
Производим повторную редукцию, в следствие чего получим матрицу:
Таблица 5
| узлы\ пункты | 1 | 2 | 3 | 5 | 6 | Сi | Аi |
| 2 | 0 | - | 14 | 26 | 32 | 0 | 14 |
| 3 | 18 | 17 | - | 4 | 0 | 0 | 4 |
| 4 | 1 | 0 | 10 | 2 | 5 | 0 | 1 |
| 5 | 1 | 40 | 20 | - | 0 | 0 | 1 |
| 6 | 16 | 0 | 0 | 0 | - | 0 | 0 |
| Cj | 0 | 0 | 0 | 0 | 0 | 0 | |
| Bj | 1 | 0 | 10 | 2 | 0 | | |
Тогда, новая нижняя граница для маршрута, включающего (1,4):

- Производим вторую итерацию решения по второй матрице.
| звено | 2,1 | 3,6 | 4,2 | 5,6 | 6,2 | 6,3 | 6,5 |
| Фij | 15 | 4 | 1 | 1 | 0 | 10 | 2 |

