<sub>Максимальный штраф выявляем у звена (2,1).

Новая нижняя граница:</sub>



Повторяем алгоритм, оптимизируя матрицу.

Итого:

Таблица 6

узлы\ пункты	2	3	5	6	Сi	Аi
3	17	-	4	0	0	4
4	0	10	2	5	0	2
5	40	20	-	0	0	20
6	0	0	0	0	0	0
Cj	0	0	0	0	0
Bj	0	10	2	0

_{Новая нижняя граница:}

.
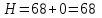_{Таким образом, в ходе решения получили маршрут (1,4), (2,1), (5,6), (3,5), (6,3), (4,2).
Маршрут будет оптимальным, если его стоимость не будет превышать стоимости любого маршрута соответствующего другим ветвлениям дерева решений.}

, значит необходимо исследовать подмножество маршрутов, не содержащих звена (1,4).

---

Значит, в исходной матрице стоимостей исключаем звено (1,4) и выполняем вышеизложенный алгоритм.

<sub>В итоге получаем дерево решений ( дальше по приложенному файлу Excel).

Определение оптимальной загрузки ВС.</sub>
Определим количество груза первого и второго типов, дающее максимальную стоимость (прибыль). Обозначим вес груза первого типа – Х1, второго – Х2. Тогда по условию задачи:

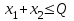, (7)

Ограничение на габариты груза приводит к неравенству:

, (8)

или

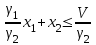, (9)
Система ограничений:



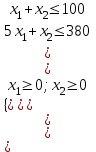
Стоимость груза: ,





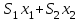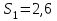
Тогда условие максимального выигрыша:



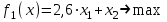
Для решения воспользуемся симплекс-методом, но предварительно нужно условия задачи записать в каноническом виде. Чтобы от неравенств перейти к равенствам введем слабые переменные:



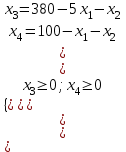
Чтобы от максимума перейти к минимуму целевой функции, условие экстремума перепишем в форме:



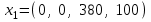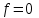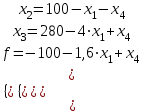
Базисным решением будет и .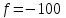



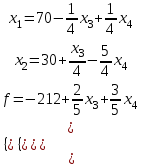
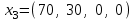и .



и .

Поскольку в целевой функции все коэффициенты при неизвестных положительные, то возможность дальнейшей минимизации f исчерпана, и мы пришли к оптимальному решению

---

.

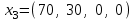
Графическое решение:



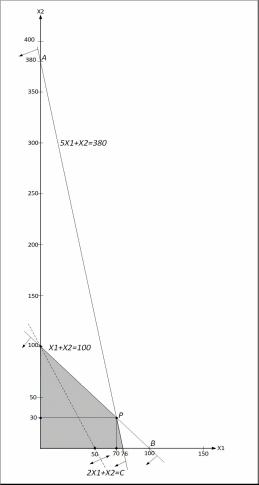
Рис.1. Геометрическое решение

---

Смотрите также файлы

• Красавица зима 1 класс.docx

• Сферификация и желефикация.pptx

• 4 курс 8 семестр Задание оформить электронное портфолио воспитателя выпускника гапоу Читинский педагогический колледж.docx

• Александр Грибоедов Горе от ума.doc

• Тест начат Вторник, 25 января 2022, 09 48.pdf