ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Автономная некоммерческая организация высшего образования
«МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»
Кафедра психологии
Форма обучения: заочная
ВЫПОЛНЕНИЕ
ПРАКТИЧЕСКИХ ЗАДАНИЙ
ПО ДИСЦИПЛИНЕ
Математические методы в психологии
МОСКВА 2021
Задание 2.
Из генеральной совокупности извлечена выборка объема n . Найти среднее значение, дисперсию, среднее квадратическое отклонение, исправленную дисперсию, коэффициент вариации, моду и медиану.
| xi | 9,5 | 10 | 10,5 | 11 | 11,5 | 12 | 12,5 |
| ni | 3 | 15 | 30 | 15 | 5 | 4 | 2 |
Решение:
Составим таблицу значений
| xi | 9,5 | 10 | 10,5 | 11 | 11,5 | 12 | 12.5 | ∑ |
| ni | 3 | 15 | 30 | 15 | 5 | 4 | 2 | 74 |
| xi ni | 28,5 | 150 | 315 | 165 | 57,5 | 48 | 25 | 780 |
| (xi – X) 2 *ni | 3 | 3,75 | 0 | 3,75 | 5 | 9 | 8 | 32,5 |
Среднее значение X = (1/n) * ∑xi ni= (1/74) * 780 = 10,5
Дисперсия D = (1/n) * ∑((xi-X)2 * ni) = (1/74) * 32,5=0,43
Исправленная дисперсия S2 = n/(n-1) * D = 74/73 * 0,43 ≈0,435
Среднеквадратичное отклонение Ỽ = √D = 0,655
Исправленное среднеквадратичное отклонение S = 0,658
Коэффициент вариации V = Ỽ/X * 100% = 0,655/10,5*100% = 0,06%
Мода – величина с наибольшей частотой Мо = 10,5
Медиана - величина, находящаяся в середине ряда Ме = 11
Задание 3
Дан следующий вариационный ряд:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Xi | 2 | 2 | 3 | 3 | 5 | 5 | 5 | 6 | 6 | 6 |
Требуется:
1) Построить полигон распределения
2) Вычислить выборочную среднюю, дисперсию, моду, медиану.
Решение: В задании дана выборка объема n = 10. Полигон
распределения – это зависимость абсолютной частоты варианта ni от
значения варианта xi. Эту зависимость можно представить в виде таблицы:
| xi | 2 | 3 | 5 | 6 |
| ni | 2 | 2 | 3 | 3 |
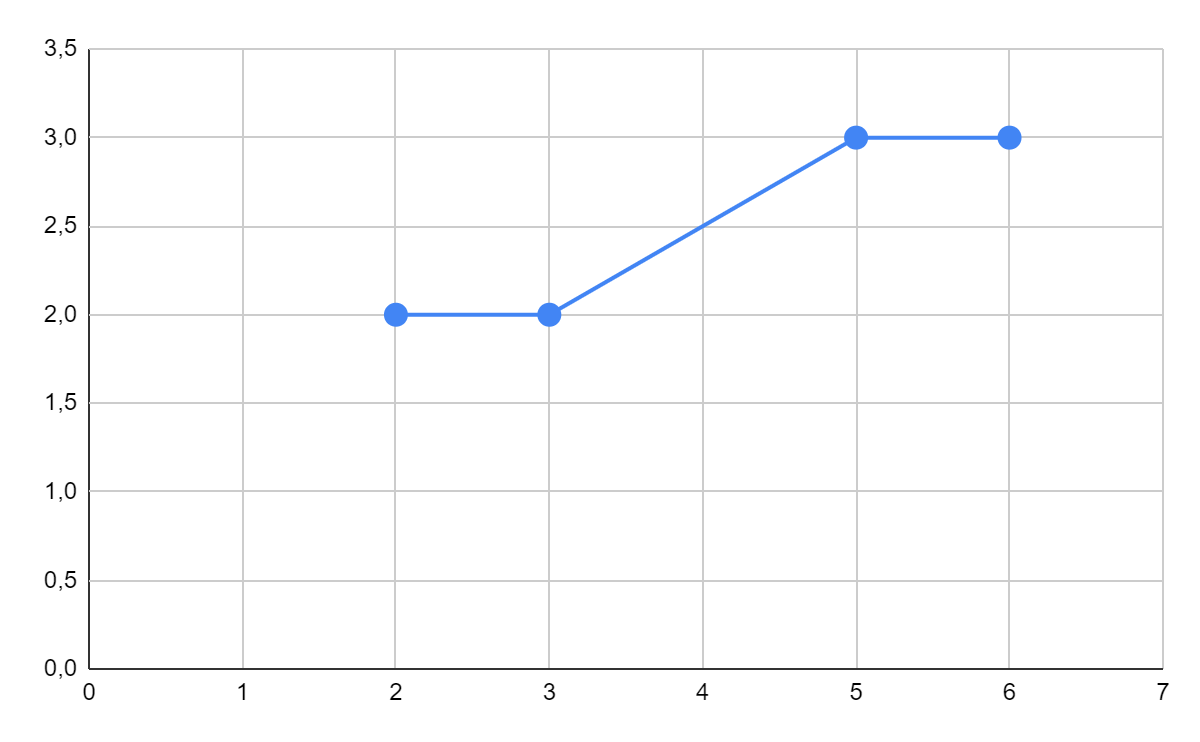
Выборочная средняя: X = 1/nΣ xi ni = 1/10(2*2+3*2+5*3+6*3) = 4,3
Выборочная дисперсия: Dx = x^2 - (x)^2 = 1/nΣ xi^2ni - 4,3^2 = 1/10(4*2+9*2+25*3+36*3) - 4,3^2 = 2,41
Мода: Mo = 5;6
Медиана: Me = 4
Задание 2.
Были протестированы две группы студентов. Тест содержал 60 вопросов. Указано число правильных ответов каждого участника теста.
Можно ли утверждать, что одна из групп превзошла другую группу по
результатам теста?
Группа 1: 55, 45, 42, 40
Группа 2: 46, 41, 38, 35, 34
Решение:
Ранжируем наблюдения:
Меньшему значению начисляется меньший ранг. Наименьшему значению начисляется ранг 1. Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений.
Количество ранжируемых значений = 4 + 5 = 9.
Минимум 34 – ранг 1. Максимум 55 – ранг 9.
Если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны.
| Группа 1 | Ранг | Группа 2 | Ранг |
| 55 | 9 | | |
| | | 46 | 8 |
| 45 | 7 | | |
| 42 | 6 | | |
| | | 41 | 5 |
| 40 | 4 | | |
| | | 38 | 3 |
| | | 35 | 2 |
| | | 34 | 1 |
| Сумма | 26 | Сумма | 19 |
Общая сумма = 9*(9+1)/2 = 45 = 26 + 19
Мы видим, что по уровню невербального интеллекта более «высоким» рядом оказывается выборка группы 1. Именно на эту выборку приходится большая ранговая сумма: 26.
Теперь мы готовы сформулировать гипотезы:
H0: Группа 1 не превосходит группу 2 по результатам теста.
Н1: Группа 1 превосходит группу 2 по результатам теста.
Определяем эмпирическую величину U:
UЭМП = (4*5)+4(4+1)/2 – 26 = 4
Ответ: Группа 1 не превосходит группу 2 по результатам теста.
Задание 3.
Психолог просит супругов проранжировать девять личностных черт, имеющих определяющее значение для семейного благополучия. Задача заключается в том, чтобы определить, в какой степени совпадают оценки супругов по отношению к ранжируемым качествам.
Решение:
| Черты личности | номер | Муж | Жена |
| Ответственность | 1 | 2 | 2 |
| Общительность | 2 | 3 | 5 |
| Сдержанность | 3 | 4 | 1 |
| Выносливость | 4 | 6 | 7 |
| Жизнерадостность | 5 | 5 | 6 |
| Терпеливость | 6 | 1 | 3 |
| Решительность | 7 | 7 | 4 |
| Оптимизм | 8 | 8 | 9 |
| Надежность | 9 | 9 | 8 |
| номер | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ∑ |
| Ранг X, dx | 2 | 3 | 4 | 6 | 5 | 1 | 7 | 8 | 9 | 45 |
| Ранг Y, dy | 2 | 5 | 1 | 7 | 6 | 3 | 4 | 9 | 8 | 45 |
| (dx – dy)2 | 0 | 4 | 9 | 1 | 1 | 4 | 9 | 1 | 1 | 30 |
p = 1 - 6 * ((Σd2) / (n3 - n) =1 - 6 * (30) / (93 - 9)) = 0,75
Ответ: Согласованность между мнениями супругов прямая и сильная.
