Файл: Сегодня финансовый анализ стал активнее и активнее использовать сложный математический инструментарий, используемый в различных точных науках, например, физике.rtf
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
) Подставить полученные параметры в уравнение для риск-нейтральной плотности вероятности
) Оценить с помощью метода Фиглевски параметры функции полезности, подставив наблюдаемые значения опционов на покупку и на продажу
Принципиальным отличием данной работы от выполненных ранее является отказ от поиска явной функции полезности Канемана. Вместо этого, мы будем различными методами искать проявлении свойств этой функции на рынке ценных бумаг.
В качестве выборки мы используем дневные котировки акций компании Goldman Sachs. Напомним, что в качестве финансовой переменной мы будем использовать нормированные цены безрисковая ставка по 10-летним американским казначейским облигациям, премии опционов от 08.05.2016 с различными ценами исполнения, для которых торговались как опционы на покупку, так и на продажу. Для опционов мы исключаем те, которые находятся далеко вне денег, имеют слишком низкое значение премии.
Параметр Q в контексте исследования означает долю безрискового актива в портфеле, поэтому он будет определяться на интервале (0;1), хотя сами психологи вкладывали в него иное значение, допускающее значения больше единицы.
Нам необходим такой параметр theta, при котором функция полезности будет принимать вид, свойственный рискофобу, это значения, превышающие 0,5.
Такое значение обусловлено условиями Канемана - Тверски, которые будут рассмотрены ниже.
Параметризация будет осуществляться методом моментов. Его суть заключается в том, что мы минимизируем квадрат отклонения моментов распределения от моментов выборки. Так как мы используем нормированные цены, то область определения будет находиться в интервале [0;2].
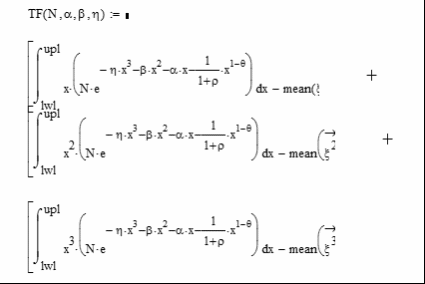
Предварительно задав начальные значения параметров для оценки, приравняв площадь под интегралом к единице, а также задав ограничения на высоту хвостов, получим вектор значений параметров:
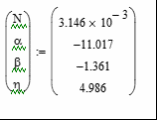
Несмотря на то, что визуально плотность выглядит почти симметрично, нельзя говорить о равном распределении увеличений и уменьшений нормированной цены. Так как рост и падение в два раза равны увеличению цены на 1 и уменьшению на 0,5. Важно будет учитывать этот нюанс, когда мы будем говорить о неодинаковом отношении к риску при росте и падении стоимости актива. Кроме того, выборка содержит 487 точек, когда стоимость актива была выше начальной цены и 848 - ниже.
5. Оценка опционов на покупку по теореме Бридена - Литценбергера
Теорема Бридена - Литценбергера говорит о том, плотность риск-нейтрального распределения равна второй производной премии оциона по цене исполнения. Если это верно, логично предположить обратное - премия опциона равна двойному интегралу риск-нейтральной функции плотности, продисконтированному к настоящему времени:
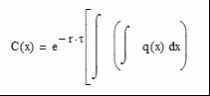
Подставив все параметры и упростив вид функции получим:

В качестве значения доли безрискового портфеля мы также, как и при параметризации, мы берем 0,8. Так как функция имеет экспоненциальный вид, то она, согласно «проклятью Эйлера», не интегрируема. Поэтому необходимо привести ее к интегрируемуму виду. Для этого воспользуемся разложением на характеристические многочлены по Гамбургеру - Ганкелю. В данной работе мы использовали 11 векторов. В результате получим следующую плотность, которая почти неотличима от исходной. Наблюдаются небольшие отклонения в хвостах распределения. Чтоб их ликвидировать, можно увеличить количество векторов. Однако нам необходимо лишь приблизительное решение, поэтому ограничимся таким видом.Так как вид функции плотности вероятности представляет собой экспоненциальную функцию (или многочлен), зависящий только от финансовой переменной, параметра Q, использовать его для оценки опционов невозможно, так как отсутствует цена исполнения.
Из-за озвученных выше проблем сложно дать разумное финансовое объяснение этой зависимости. На данном графике мы видим, что при росте цены актива выше текущей цены, мы видим экспоненциальный рост премии опциона. Этот результат требует дальнейшего изучения, так как при понимании, как оценивать таким методом опционы на конкретную цену исполнения, можно получить достаточно простой метод оценки.
Данная проблема решена в работе Стивена Фиглевски. Он дает следующее определение премии опциона:
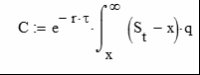
Здесь St - текущая цена подлежащего активаx - цена исполнения опциона
r - безрисковая ставка
thau - время до исполнения
Используя рыночные данные по опционам на акции Goldman Sachs, мы можем оценить параметры риск-нейтральной функции плотности вероятности. Для этого оценим все параметры используемой функции на опционах на покупку и на продажу методом наименьших квадратов:
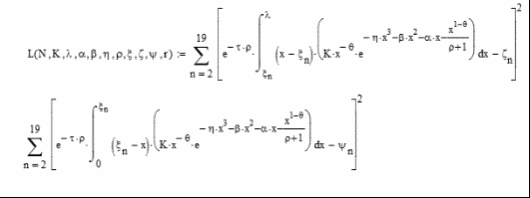
Данная процедура выполнена на опционах с разными датами до погашения в приложении 5.

Где y1 - вектор параметров для опционов с датой исполнения на 20.01.2017, y2 - на 21.10.2016 и y3 - 20.05.2016.
Мы видим, что плотность эволюционирует со временем, что позволяет оценить, как отношение к риску зависит от временного горизонта.
Теперь, когда мы имеем необходимую методологию для решения поставленной задачи, рассмотрим теорию перспектив, а также свойства функции полезности.
. Теория перспектив Дэниэля Канемана
Чтобы оценить функцию полезности, мы должны вменить ей какие-то свойства, иначе оценить константы в решении дифура не представляется возможным. Для этого мы рассмотрим теорию перспектив Дэниэля Канемана, где с помощью эмпирического исследования он выявил определенные свойства для функции полезности экономических агентов.
Она исходит из того, что традиционная теория ожидаемой полезности не выдерживает эмпирической проверки. Это было доказано Морисом Алле, когда он выдвинул свой парадокс Алле.
Тогда Дэниэль Канеман и Амос Тверски с помощью опросов провели эксперимент, который должен был определить способы принятия решений в условиях неопределенности. Рассмотрим некоторые задачи, рассмотренные в их работе, которые дают нам определенные свойства функции полезности:
Таблица 1
| | Игра на плюс | Игра на минус |
| Задача 1 N=95 | (4000;0,80)<(3000;1) [20] [80] | (-4000;0,80)>(-3000;1) [92] [8] |
| Задача 2 N=95 | (4000;0,20)>(3000;0,25) [65] [35] | (-4000;0,20)<(-3000;0,25) [42] [58] |
| Задача 3 N=66 | (3000;0,90)>(6000;0,45) [86] [14] | (-3000;0,90)<(-6000;0,45) [8] [92] |
| Задача 4 N=66 | (3000;0,002)<(6000;0,001) [27] [73] | (-3000;0,002)>(-6000;0,001) [70] [30] |
Количество респондентов обозначено за N, в квадратных скобках дано процентное количество, выбравшее ту или иную лотерею.
Как видно из таблицы, предпочтения в левой части являются зеркальным отражением правой. Исходя из этого, делаются три главных вывода:
· избегание риска в случае игры на плюс заменяется склонностью к риску в случае возможных убытков;
· как в правой части таблицы, так и в левой нарушаются принципы теории ожидаемой полезности;
· эффект отражения отвергает идею о том, что избегание неуверенности объясняет эффект уверенности, скорее уверенность усиливает избегание потерь в той же степени, что и стремление к выигрышу.
Теперь рассмотрим процесс принятия решений согласно Канеману и Тверски:
Теория разделяет весь процесс принятия решения на две стадии: редактирование и оценка. Стадия оценки заключается в предварительном анализе предложенных альтернатив, который направлен на их упрощение. Далее отредактированные возможности оцениваются, и выбирается наиболее ценная.
Стадия редактирования состоит из 4 основных операций:
. Кодирование. Как было сказано выше, агент делает выбор, основываясь на изменении его благосостояния, а не на конечном его уровне. Следовательно, сначала определяется некая отправная точка, относительно которой измеряется изменение. Затем возможные исходы лотереи кодируются как доходы или убытки. Естественно, что на это влияет формулировка лотереи и ожидания агента, принимающего решение.
. Комбинирование. Лотереи иногда могут упрощаться комбинированием возможностей с одинаковыми исходами. Например, лотерея (200, 0,25 ;200, 0,25) будет упрощена до (200, 0,50) и будет оцениваться в такой форме.
. Сегрегация. Если игра содержит одновременно рисковый и безрисковый компонент, то они будут отделены друг от друга. Например, лотерея (300, 0,80; 200, 0,20) будет преобразована в лотерею с безрисковой составляющей 200 и рисковой - (100, 0,80). Аналогично для игр с отрицательными исходами.
. Отклонение. Респонденты склонный игнорировать некоторые альтернативы или стадии выбора, если в альтернативах есть схожие компоненты. Например, выбор между (200, 0,20;100, 0,50; -50, 0,30) и (200, 0,20;150, 0,50; -100, 0,30) уменьшается до (100, 0,50; -50, 0,30) и (150, 0,50;-100, 0,30).
. Получение свойств функции ценности (полезности)
Существенная особенность теории перспектив заключается в том, что акцент делается на важность изменения благосостояния агента, а не на конечное благополучие. Это предположение совместимо с основными принципами восприятия и суждения. Наш аппарат восприятия намного более чувствителен к изменениям, чем к оценке абсолютных значений величин. Например, при похолодании с +20С до +5С, человек будет ощущать холод сильнее, чем при похолодании с +5С до 0. Здесь снова стоит вспомнить о важности исходной точки: агент адаптируется к начальным условиям, а затем весь полученный опыт, все изменения текущего состояния и прочее сравнивает с исходным состоянием. Тоже самое и для финансового благосостояния: для кого-то потеря 1000$ является шагом в бедность, а для кого-то - лишь незначительным убытком. Все зависит от отправной точки. Важным является и отношение к размеру изменений. Очевидно, что разница в ценности получения 100$ и 200$ значительно выше, чем между 1100$ и 1200$, аналогично для убытков. Видно, что субъективная ценность изменений выше, чем модальное изменение. Отсюда получается форма функции изменения стоимости: она вогнутая, когда богатство увеличивается относительно исходной точки (υ’’(x)<0, для x>0), и выпуклая для убытков (υ’’(x)<0, для x<0). Такой вывод делается исходя из ответов респондентов на безрисковые альтернативы. Пример ниже покажет, что те же свойства характерны и в случае принятия решений в условиях риска.
Таблица 2
| | A | B |
| | 6000 с вероятностью 0,25 | 4000 с вероятностью 0,25 или 2000 с вероятностью 0,25 |
| N=68 | [18] | [82] |
| | C | D |
| | -6000 с вероятностью 0,25 | -4000 с вероятностью 0,25 или -2000 с вероятностью 0,25 |
| N=64 | [70] | [30] |
Подставляя эти условия в уравнение:
π(0,25)υ(6000)<π(0,25)[ υ(4000)+ υ(2000)] и
π(0,25) υ(-6000)>π(0,25)[ υ(-4000)+ υ(-2000)].
Сокращая π(0,25) получается, чтоυ(6000)<υ(4000)+υ(2000) и υ(-6000)>υ(-4000)+υ(-2000). Таким образом, получается, что функция ценности в условиях риска обладает теми же свойствами, что и без риска.
Здесь нужно сделать оговорку. Канеман и Тверски делают разграничение между функцией ценности и функцией полезности в силу неоднозначного отношения агентов к денежному богатству. Для упрощения это предположение не будет играть роли в дальнейшем исследовании, так как для получения рискофобного распределения с помощью теоремы Пратта-Эрроу необходимо использовать функцию полезности.
Еще раз запишем свойства функции ценности:
· Дважды дифференцируема
· непрерывна
· y=0
· υ(x)<-υ(-x)
· υ’(x)<υ’(-x)
· υ’’(x)<0
· υ’’(-x)>0
Таким образом, функция ценности, согласно теории перспектив будет выглядеть следующим образом:
8. Использование свойств функции полезности Канемана - Тверски для прогнозирования финансовых рынков
Ранее мы использовали свойства функции полезности, в качестве ограничений для дифференциального уравнения второго порядка, чтобы получить ее в явном виде. Так как такой цели перед нами больше не стоит, мы попробуем обнаружить эти поведенческие особенности принятия решения на финансовом рынке. Для этого выдвигается следующая гипотеза: из-за несимметричного отношения к риску при росте и при падении цены, позиции закрываются при меньшем изменении стоимости позиции в первом случае и большем - во втором. Иными словами, мы для закрытия позиции в случае увеличения ее стоимости необходимо меньшее изменение цены, чем при ее падении.


