σ_sp – предварительное напряжение в арматуре с учетом всех потерь и коэффициента γ_sp = 0,9.

Принимаем σ_sp = 0,8 R_sn = 0,8x600 = 480 МПа = 0,8x6100 = 4880 кг/см²

При проектировании конструкции полные суммарные потери следует принимать не менее 100 МПа. ∆σ_sp(2)j = 100 МПа = 1020 кг/м².

П
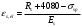
ри определении :

σ_sp = 0,9 x 4880 – 1020 = 3372 кг/м²







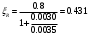
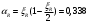
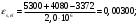
П
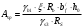
лощадь сечения арматуры определяется по формуле:

Е
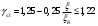
сли соблюдается условие 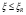, расчетное сопротивление напрягаемой арматуры R_S допускается умножить на коэффициент условий работы γ_s3, учитывающий возможность деформирования высокопрочных арматурных сталей при напряжениях выше условного предела текучести и определяемый по формуле:

Е
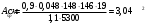
сли 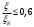, что для плит практически всегда соблюдается, можно принимать максимальное значение этого коэффициента, т. е. γ_s3 = 1,1.

Принимаем 6Ø10 А600; А_гр = 4,71 см².

Напрягаемые стержни должны располагаться симметрично и расстояние между ними должно быть не более 400 мм при h> 150 мм.

---

Расчет по прочности при действии поперечной силы



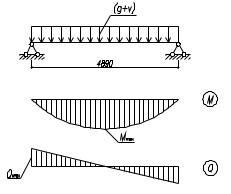
Поперечная сила от полной нагрузки Q = 2677 кг.

Р
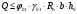
асчет предварительно напряженных элементов по сжатой бетонной полосе между наклонными сечениями производят из условия:

φ_b1 – коэффициент, принимаемый равным 0,3

b
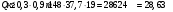
– ширина ребра, b = 37,7 см;

Р
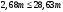
асчет предварительно напряженных изгибаемых элементов по наклонному сечению производят из условия:

Q ≤ Q_b + Q_sw

Q – поперечная сила в наклонном сечении;

Q_b– поперечная сила, воспринимаемая бетоном в наклонном сечении, принимается не более 2,5γ_b1 R_bt b h₀ и не менее 0,5γ_b1 R_bt b h₀

Q



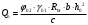
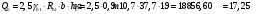
_sw – поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении;

φ_b2 – коэффициент, принимаемый равным 1,5

Следовательно, поперечная сила, воспринимаемая бетоном, имеет большее значение, чем действующая в сечении поперечная сила, поэтому поперечную арматуру можно не устанавливать.

2.3. Расчет плиты по предельным состояниям второй группы

Геометрические характеристики приведенного сечения

---

Круглое очертание пустот заменяется эквивалентным квадратным со стороной

с = 0,9·d = 0,9·15,9 = 14,3 см.

Размеры расчетного двутаврового сечения:

толщина полок: h’_ƒ= h_ƒ = (22 – 14,3)·0,5 = 3,85 см;

ширина ребра b = 146 – 14,3·7 = 45,9 см;

ширина полок b’_ƒ =146 см; b_ƒ = 149 см.

Определяем геометрические характеристики приведенного сечения:

α = E_s/E_b = (2·10⁶)/30,6·10⁴ = 6,54.

Площадь приведенного сечения:

A_red = A + αA_s = b’_ƒ ·h’_ƒ + b_ƒ ·h_ƒ + b·c + αA_s = (146 + 149)·3,85 + 45,9·14,3 + 6,54·4,71 = 1823 см²; А = 1792 см² – площадь сечения бетона.

Статический момент приведенного сечения относительно нижней грани:

S_red = b’_ƒ ·h’_ƒ· (h - 0,5·h’_ƒ) + b_ƒ ·h_ƒ · 0,5·h_ƒ + b·c·0,5·h + α·A_s·a =

= 146·3,85·(22 – 0,5·3,85) + 149·3,85·0,5·3,85 + 45,9·14,3·0,5·22 + 6,54·4,71·3 =

= 11284,16 + 1104,28 + 7220,07 + 92,41 = 19701 см³.

Удаление центра тяжести сечения от его нижней грани:

y₀ = S_red/A_red = 19701/1823 = 10,807 ≈ 10,8 см.

Момент инерции приведенного сечения относительно его центра тяжести:

I_red = 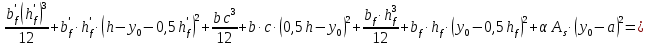(146·3,85³)/12 + 146·3,85· (22 – 10,8 – 0,5·3,85)² + (45,9·14,3³)/12 + 45,9·14,3·(0,5·22 – 10,8)² + (149·3,85³)/12 + 149·3,85·(10,8 – 0,5·3,85)² + 6,54·4,71·(10,8 – 3)² = 694,3 + 48355,0 + 11185,1 + 26,3 + 708,6 + 45183,9 + 1874,08 =

= 108027см⁴

Момент приведенного сечения по нижней грани:

W_red = I_red/y₀ = 108027/10,8 = 10003 см³.

То же, по верхней грани:

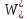= I_red/(h – y₀) = 108027/(22 – 10,8) = 9645 см³.

Расчет предварительно напряженных изгибаемых элементов по раскрытию трещин производят в тех случаях, когда соблюдается условие: M > M_crc

M – изгибающий момент от внешней нагрузки (нормативной);

M_crc – изгибающий момент, воспринимаемый нормальным сечением элемента при образовании трещин и равный:

M_crc = R_bt,ser ·W + P·e_яр, где

W – момент сопротивления приведенного сечения для крайнего растянутого волокна;

---

е_яр = е_ор + r– расстояние от точки приложения усилия предварительного обжатия до ядровой точки, наиболее удаленной от растянутой зоны;

е_ор– то же, до центра тяжести приведенного сечения;

r - расстояние от центра тяжести приведенного сечения до ядровой точки;

W = 1,25 · W_redдля двутаврового симметричного сечения;

P – усилие предварительного обжатия с учетом потерь предварительного напряжения в арматуре, соответствующих рассматриваемой стадии работы элемента. Определяем:

r = W_red/A_red= 10003/1823 = 5,49 см;

е_ор = y₀ – a= 10,8 – 3 = 7,8 см;

е_яр= 7,8 + 5,49 =13,29 см;

W= 1,25·10003 = 12504 см³.
Потери предварительного напряжения арматуры.

Потери от релаксации напряжений арматуры Δσ_sp1определяют для арматуры класса А600 при электромеханическом способе натяжении в соответствии с п.2.2.3.3 СП 52-102-2004.

Δσ_sp1 = 0,03·σ_sp = 0,03·4880 = 146, 4 кг/см².

Потери от температурного перепада при агрегатно-поточной технологии принимаются равными 0; Δσ_sp2 = 0.

Потери от деформации формы при электротермическом способе натяжения арматуры не учитывают; Δσ_sp3 = 0.

Потери от деформации анкеров при электротермическом способе натяжения арматуры не учитывают; Δσ_sp4 = 0.

Первые потери:

Δσ_sp(1) = Δσ_sp1 + Δσ_sp2 +Δσ_sp3 +Δσ_sp4 = 146,4 кг/см².

Потери от усадки бетона:

Δσ_sp5 = σ_b,sh·E_s

σ_b,sh – деформации усадки бетона, значение которого можно принять в зависимости от класса бетона (В25) равным: 0,0002

Δσ_sp5 = 0,0002·2·10⁶ = 400 кг/см².

Потери от ползучести бетона Δσ_sp6 определяются по формуле:

Δσ_sp6 = 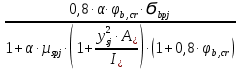, где

α = 6,54

φ_b,

---

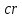
– коэффициент ползучести бетона. φ_b, = 2,5;

σ_bpj - напряжение в бетоне на уровне центра тяжести рассматриваемой j-ой группы стержней напрягаемой арматуры;

σ_bp = P₍₁₎/A_red + (P₍₁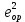₎ )/I_red;

P₍₁₎ – усилие предварительного обжатия с учетом только первых потерь;

е_ор – эксцентриситет усилия P₍₁₎ относительно центра тяжести приведенного сечения;

µ_spj – коэффициент армирования, равный A_spj/A, где А – площадь поперечного сечения элемента;

А_spj – площадь рассматриваемой группы стержней напрягаемой арматуры.

P₍₁₎ = A_sp(σ_sp – Δσ_sp(1)); σ_sp = 4880 кг/см²;

Δσ_sp(1) = 146,4 кг/см²; Р₍₁₎ = 4,71(4880 – 146,4) = 22295 кг;

е_ор = 7,8 см; I_red = 108027

σ_bp = 22295/1823 + (22295·7,8²)/ 108027 = 24,79 кг/см²;

А = 1792 см²; µ = 4,71/1792 = 0,0026;

Δσ_sp6 = 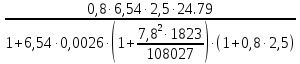= 294 кг/см².

Полное значение первых и вторых потерь:

Δσ_sp(2) = 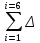σ_spi

Δσ_sp(2) = 146,4 + 400 + 294 = 840,4 кг/см².

При проектировании конструкций полные суммарные потери для арматуры расположенной в растянутой при эскплуатации зоне сечения элемента, следует принимать не менее 100 МПа (п. 2.2.3.9 СП 52-102-2004), поэтому принимаем Δσ_sp(2) = 1000 кг/см².

После того, как определены суммарные потери предварительного напряжения арматуры, можно определить М_crc.

Р₍₂₎ = (σ_sp – Δσ_sp(2))·A_sp;

P₍₂₎ – усилие предварительного обжатия с учетом полных потерь;

Р₍₂₎ = (4880 – 1000)·4,71 = 18275 кг;

М_crc = R_bt,ser·W + P₍₂₎·e_яр = 15,8·12504 + 18275 ·13,29 = 440438 кг·см = 4405

---

Смотрите также файлы

• Расчетный листок за Январь 2023 г.docx

• Есть идея! Голодные игры в библиотеке в ноябре Липецкой областной научной библиотеке исполняется 95 лет. И именно поэтому библиотека решила подарить липчанам новый образовательный квест Голодные игры.docx

• Введение в информационные технологии.docx

• Задание Учреждения по организации отдыха и оздоровления детей в период каникул оказывают различные услуги.docx

• 1)В каком году был построен дк им. Ильича (1959 г.) 2)Кто был основателем Охотского краеведческого музея (Евгений Федорович Мороков 1962г.).docx