Практическое занятие № 9

«Решение комбинаторных задач».

Методы решения комбинаторных задач:

1. 
   метод перебора;
   
2. 
   табличный метод (все условия вносятся в таблицу, в ней же выполняется решение);
   
3. 
   построение дерева возможных вариантов решений;
   
4. 
   построение графа.
   

1. Метод перебора возможных вариантов

Простые задачи решают обыкновенным полным перебором возможных вариантов без оставления различных таблиц и схем.

Способ перебора может применяться в простых задачах, например в таких, как эта:

Задача 1. Для своих двух книг Маша купила три разные обложки. Сколькими различными способами она может обернуть книги купленными обложками?

Ответ: Для решения обозначим обложки буквами а, б, в. Составим из букв всевозможные пары: аб, ав, бв, ба, ва, вб. Всего получилось 6 способов.

Задача 2. Какие двузначные числа можно составить из цифр 1, 2, 3, 4, 5?

Ответ: 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43,

44, 45, 51, 52, 53, 54, 55
2. Табличный метод

Решить комбинаторные задачи можно с помощью таблиц. Они, как и дерево возможных вариантов, наглядно представляют решение таких задач.

Задача 3. Сколько нечетных двузначных чисел можно составить из цифр 1, 3, 4, 6, 7, 8, 9?

Решение. Составим таблицу: слева первый столбец - первые цифры искомых чисел, вверху первая строка - вторые цифры.

	1	3	4	6	7	8	9
1	11	13	14	16	17	18	19
3	31	33	34	36	37	38	39
4	41	43	44	46	47	48	49
6	61	63	64	66	67	68	69
7	71	73	74	76	77	78	79
8	81	83	84	86	87	88	89
9	91	93	94	96	97	98	99

---

В таблице показаны все возможные варианты решения данной задачи. Выбираем все нечетные числа – это первый, второй, пятый и седьмой столбец. Всего получается 28 вариантов.

Ответ: 28

Задача 3. Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.

Решение. Составим таблицу: слева первый столбец - имена девочек, вверху первая строка - имена мальчиков.

	Андрей	Миша	Игорь
Маша	Андрей - Маша	Миша - Маша	Игорь - Маша
- Оля	Андрей - Оля	Миша - Оля	Игорь - Оля
Вера	Андрей - Вера	Миша - Вера	Игорь - Вера
Ира	Андрей - Ира	Миша - Ира	Игорь - Ира

Все возможные варианты перечисляются в строках и столбцах таблицы. Всего 12 вариантов.

Ответ: 12 вариантов.
3. Построение дерева возможных вариантов

Задача 4. Катя собирается на каникулы. Она может поехать с бабушкой или с родителями. Если Катя поедет с бабушкой, то она сможет провести каникулы или на даче, или в городе, или в деревне. Если она поедет с

родителями, то она сможет провести каникулы или отдыхая в санатории, или путешествия по горам, или путешествуя на теплоходе. Сколько разных вариантов есть у Кати, чтобы провести свои каникулы?

Решение:


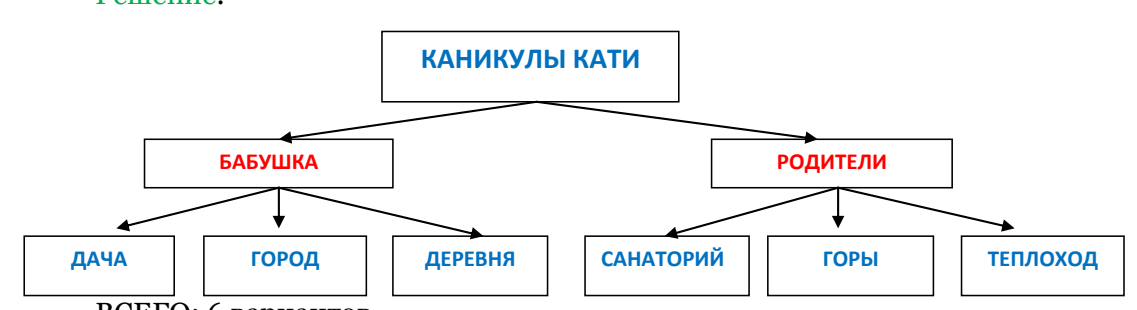
ВСЕГО: 6 вариантов .
4. Метод построения графа

---

Граф - это геометрическая фигура, состоящая из точек (вершины графа) и линий, их соединяющих (рѐбра графа). При этом с помощью вершин изображают элементы некоторого множества (предметов, людей и т.д.), а с помощью рёбер - определённые связи между элементами. Для удобства иллюстрации условия задачи, вершины графа могут быть заменены кругами или прямоугольниками.
Задача 5. Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно?



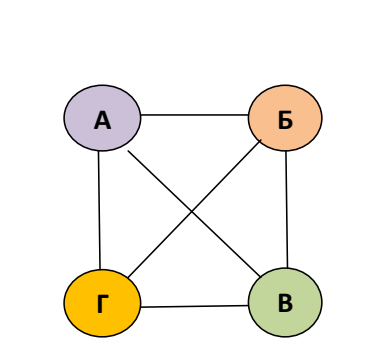
Ответ: 6 партий.
Задача 6. Вася, Коля, Петя, Аня и Наташа - лучшие лыжники в пятом классе. Для участия в соревнованиях нужно выбрать из них одного мальчика и одну девочку. Сколькими способами это можно сделать?


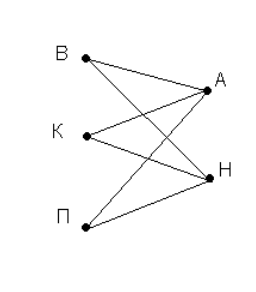
Ответ: 6 способов.


Задания для практической работы:

Решить задачи методом перебора:

1. Сколькими способами из цифр 1, 2, 3, 4 можно составить число, кратное 6? При составлении числа каждую цифру можно использовать один раз или не использовать совсем.

2. Маша собирается съесть яблоко, сливу и мандарин, но пока не решила, в какой последовательности. Сколькими способами Маша может выбрать эту последовательность?

3. В кружок бального танца записались: Петя, Коля, Витя, Олег, Таня, Оля, Наташа, Света. Какие танцевальные пары девочки и мальчика могут образоваться?

4. В финальном забеге на 100 м участвуют Иванов, Громов и Орлов. Назовите возможные варианты распределения призовых мест.

5. Какие трехзначные числа можно составить из цифр 0, 2, 4? Цифры могут повторяться.

6. Сколько существует флагов составленных из трех горизонтальных полос одинаковой ширины и разных цветов - красный, белый, зеленый, синий.

7. Четыре гостя при входе в ресторан отдали швейцару свои шляпы, а при выходе получили их обратно. Невнимательный швейцар раздал шляпы случайным образом. Сколько существует вариантов, при которых каждый гость получил чужую шляпу?
Решить задачи табличным способом:

8. Имеется 5 видов конвертов без марок и четыре вида марок одного достоинства. Сколькими способами можно выбрать конверт с маркой для посылки письма?

---

9. Сколькими способами можно выбрать гласную и согласную буквы из слова «камзол»?

10. Сколько нечетных чисел можно составить из цифр числа 3694 (каждую цифру можно использовать не более одного раза)?

11. На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром. Из скольких вариантов завтрака Вова может выбирать?

12. У Светланы 3 юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций из юбок и кофт имеется у Светланы?

13. У Светланы 3 юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций из юбок и кофт имеется у Светланы?

14. Чтобы попасть из города А в город Б, нужно по дороге доехать до реки, а затем переправиться на другой ее берег. До реки можно доехать на мотоцикле, на автобусе,

на автомобиле или дойти пешком. Через реку можно переправиться либо вплавь, либо переплыть на лодке, либо — на пароме. Сколько существует различных способов добраться из города А в город Б?
Решение задач с помощью графа:

15.Ужасные грабители Кнопка и Скрёпка решили украсть из сейфа золотой ключик Буратино, который знает пока 4 цифры:1,2,3,4.Сколько вариантов придётся перебрать им, чтобы проникнуть в дом, подобрав двузначный код?

16. Сколько различных завтраков, состоящих из 1 напитка и 1 вида выпечки, можно составить из чая, кофе, булочки, печенья и вафель?

17. Шесть семей уехали отдыхать в разные города. Приехав к месту отдыха, они поговорили друг с другом по телефону. Сколько звонков было сделано?

18. На отрезке АВ, и отметили на нем 4 точки: М,С,К,Д. Сколько отрезков на чертеже?
Решить задачу с помощью дерева возможных вариантов:

19. в среду 4 урока: математика, информатика, русский язык, английский язык. Сколько можно составить вариантов расписания на среду?

20. В 6 классе в четверг 5 уроков: математика, информатика, русский язык, английский язык, физкультура. а) Сколько имеется вариантов расписания при условии, что физкультура – последний урок? б) Сколько имеется вариантов расписания при условии, что физкультура – последний урок, а математика – первый?

---

21. Саша ходит в школу в брюках или джинсах, к ним одевает рубашки серого, голубого, зеленого цвета или в клетку, а в качестве сменной обуви берет туфли или кроссовки.а) Сколько дней Саша сможет выглядеть по-новому?б) Сколько дней при этом он будет ходить в кроссовках?в) Сколько дней он будет ходить в рубашке в клетку и джинсах?

---

Смотрите также файлы

• Кні Педагогті атыжні.docx

• Занятие 3 Студентка группа Преподаватель Пермь 2020.docx

• AnalogWrite(pin, value).docx

• Химия 8 сынып 1нса Мына берілгендерді ішінде крделі заттара жататындары.docx

• Крінетін белгілері Сипаттамалары.doc