Файл: Урок по теме Квадратные уравнения. Вы уже умеете решать квадратные уравнения различными способами. Давайте попробуем определить цели нашего.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.03.2024
Просмотров: 10
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
теорема виета
Цели: изучить теорему Виета; формировать умение применять теорему Виета и обратную ей теорему при решении приведённых квадратных уравнений.
Ход урока
I. Организационный момент.
II. Устная работа.
Ребята, сегодня у нас очередной урок по теме «Квадратные уравнения». Вы уже умеете решать квадратные уравнения различными способами.
Давайте попробуем определить цели нашего сегодняшнего урока, что мы уже
умеем делать, чему должны или можем научиться. Итак…
| О квадратных уравнениях | ||
| № п/п | Что я знаю | Что не знаю |
| 1. 2. 3. | Решать по формуле полные квадратные уравнения Решать неполные квадратные уравнения Решать задачи с помощью квадратных уравнений | Новый способ решения квадратных уравнений |
Выслушать предложения ребят, скорректировать ответы, сделать выводы и сформулировать цели урока.
Напишите в тетрадях дату, классная работа, тему урока: Теорема Виета.
Актуализация опорных знаний:
на доске записаны квадратные уравнения:
х2 – 13х + 12 = 0;
9 – 2х2 – 3х = 0;
х2 + 8х + 7 = 0;
3х2 – 2х = 4;
6х2 – 2 = 6х;
х2 = - 9х – 20.
Ответьте на следующие вопросы.
Назовите номер уравнения записанного в стандартном виде (1;3)
Назовите номер уравнения, не приведенного к виду ax2+ bx+ c= 0 (2,4,5,6)
Назовите номер уравнения, в котором коэффициент b – четное число (3,4,5)
Назовите номер уравнения, в котором коэффициент b – нечетное число (1,2,6)
Назовите номер уравнения, у которого коэффициент а = 1 (1,3,6)
Как называется квадратное уравнение, у которого коэффициент а = 1. (приведенное)
III. Объяснение нового материала.
Объяснение проводится в н е с к о л ь к о э т а п о в.
1. «О т к р ы т и е» теоремы Виета.
Целесообразно организовать лабораторную исследовательскую работу. Для этого разбить класс на пять групп, каждой из которых дать решить приведённое квадратное уравнение. После его решения один представитель от каждой группы выходит к доске и заполняет соответствующую строку в таблице:
| № | Уравнение | Корни уравнения | Сумма корней | Произведение корней |
| 1 | х2 + х –12 = 0 | | | |
| 2 | х2 – 12х – 45 = 0 | | | |
| 3 | у2+ 8у +15 = 0 | | | |
| 4 | у2– 5у +6 = 0 | | | |
| 5 | z2–10z +21 = 0 | | | |
| 6 | z2– 3z –10 = 0 | | | |
После этого учитель предлагает учащимся сравнить сумму и произведение полученных корней с коэффициентами b и c и выдвинуть гипотезу. Учитель подтверждает сделанное предположение, сообщая, что данное утверждение называется теоремой Виета
, обращая внимание учащихся, что эта теорема справедлива для приведенных квадратных уравнений.
Вопрос. Можем ли мы сделать предположение о связи между корнями приведенного квадратного уравнения и его коэффициентами?
(х1+х2 = -р, х1•х2 =q.)
(Проведенное исследование позволяет учащимся высказать гипотезу о связи между корнями и коэффициентами приведенного квадратного уравнения.)
| Т е о р е м а В и е т а Если х1, х2 – корни уравнения x2 + px + q = 0, то х1 + х2 = –р; х1 · х2 = q. |
2. Т е о р е м а В и е т а для неприведённого квадратного уравнения.
При выполнении устной работы в начале урока учащиеся вспомнили, как преобразовать квадратное уравнение в приведённое. Следует предложить им самостоятельно вывести формулы для неприведённого квадратного уравнения, используя теорему Виета. После этого на доску выносится запись:
| Т е о р е м а В и е т а Если х1, х2 – корни уравнения аx2 + bx + c = 0, то х1 + х2 = |
3. Т е о р е м а, обратная теореме Виета.
Обращаем внимание учащихся, что по теореме Виета мы можем только убедиться в правильности нахождения корней с помощью дискриминанта. Возникает вопрос, а если мы подберем такие числа, которые в сумме будут равны второму коэффициенту с противоположным знаком, а в произведении – свободному члену, то не будут ли они являться корнями уравнения? Подчеркиваем, что мы хотим воспользоваться утверждением, обратным теореме Виета, значит, мы должны его доказать. Работа с теоремой Виета и обратной ей теоремой позволяет формировать элементы математической культуры учащихся.
После рассмотрения (по учебнику) доказательства теоремы привести примеры нахождения корней квадратного уравнения подбором.
IV. Формирование умений и навыков.
Все упражнения, выполняемые на этом уроке, можно разбить на две группы:
1-я г р у п п а. Упражнения на непосредственное применение теоремы Виета.
2-я г р у п п а. Упражнения на нахождение подбором корней приведённого квадратного уравнения.
1. № 580 – устно.
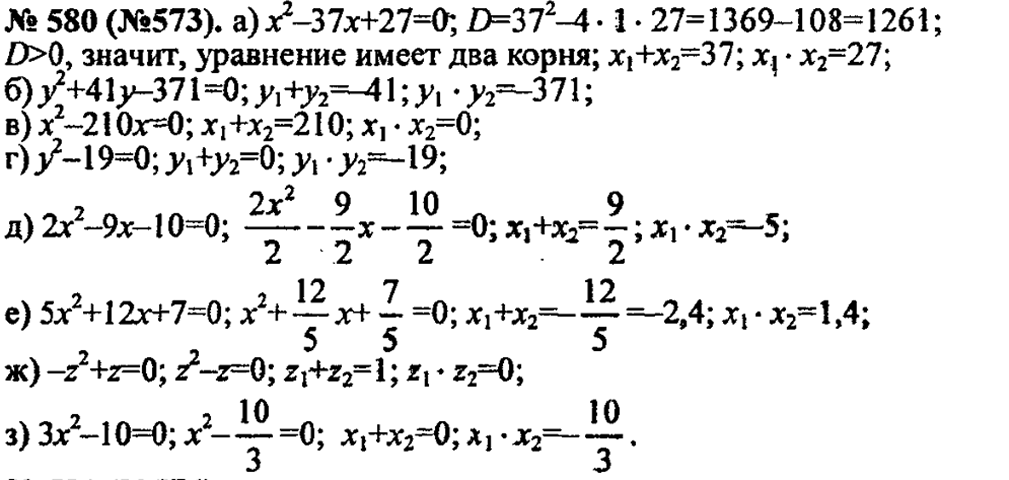
2. № 581 (а, в), № 582 (а, б, г, д).
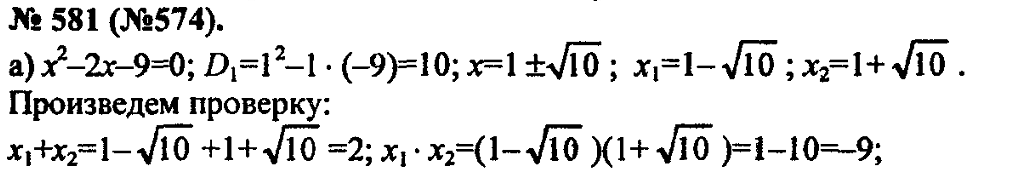
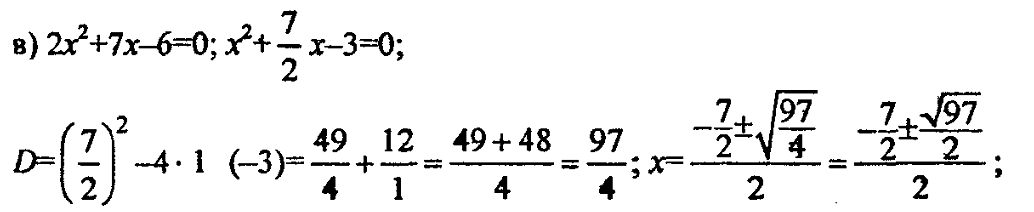
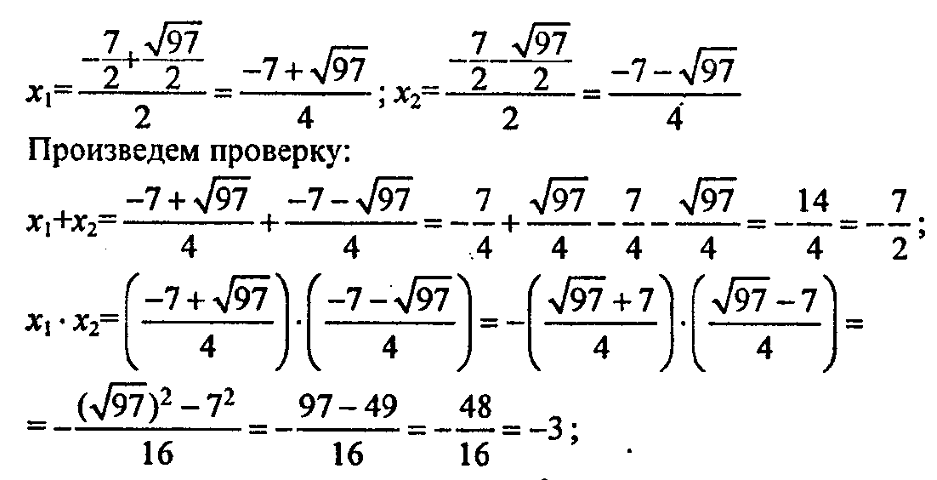
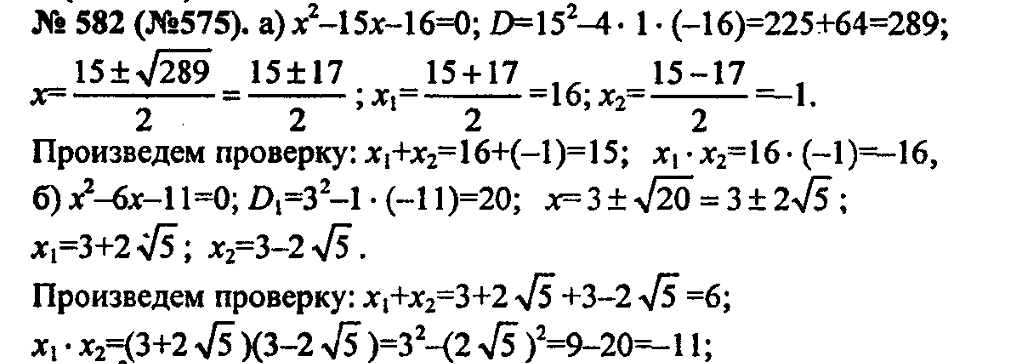
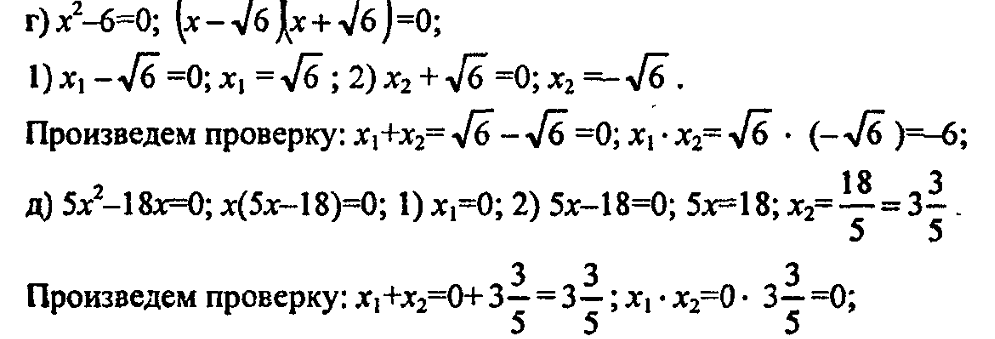
3. Решите квадратное уравнение по формуле и сделайте проверку, используя теорему Виета:
а) х2 + 7х – 8 = 0; в) х2 – 4х – 5 = 0;
б) х2 – 5х – 14 = 0; г) х2 + 8х + 15 = 0.
4. № 583 (а, в).
5. Найдите подбором корни уравнения:
а) х2 – 11х + 28 = 0; г) х2 + 3х – 28 = 0;
б) х2 + 11х + 28 = 0; д) х2 + 20х + 36 = 0;
в) х2 – 3х – 28 = 0; е) х2 + 37х + 36 = 0.
V. Проверочная работа. (резерв)
Каждое из следующих уравнений имеет по два корня: х1 и х2. Не находя их, найдите значение выражений х1 + х2 и х1 · х2:
а) х2 – 7х – 9 = 0; в) 5х2 – 7х = 0;
б) 2х2 + 8х – 19 = 0; г) 13х2 – 25 = 0.
VI. Итоги урока.
В о п р о с ы у ч а щ и м с я:
- Чем лично для вас был интересен этот урок?
- Какие формы работы вам понравились?
- На каком этапе урока вы испытывали затруднения?
- Где вы видите практическое применение изученной теоремы?
- Как вы думаете, над какими вопросами данной темы нам предстоит еще работать?
Домашнее задание: № 581 (б, г), № 582 (в, е), № 583 (б, г), № 584.
Д о п о л н и т е л ь н о: найти подбором корни уравнения:
а) х2 – 12
х + 27 = 0; в) х2 + 9х – 36 = 0;
б) х2 + 6х – 27 = 0; г) х2 – 35х – 36 = 0.

