Файл: 2 величина признака, которая чаще всего встречается в данной совокупности.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.03.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант 1.
1.1. Отметьте правильное определение моды:
1) величина, которая находится в середине вариационного ряда;
2) величина признака, которая чаще всего встречается в данной совокупности;
3) величина, равная средней арифметической из значений признака.
1.2. Относительная величина – это обобщающий показатель, который:
1) характеризует общий уровень признака данной совокупности;
2) дает числовую меру соотношения двух сопоставляемых статистических величин;
3) показывает различие значений признака у разных единиц совокупности в один и тот же период времени.
1.3. Коэффициент вариации рассчитывается по значениям
1) разных характеристик одного и того же признака в одной совокупности;
2) разных признаков в разных совокупностях;
3) одного и того же признака в разных совокупностях.
1.4. По 5 выборочным наблюдениям вычислены значения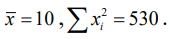 
Значение несмещенной оценки дисперсии равно:
1) 7,5 2) 30 3) 6.
1.5. По данным выборочного обследования 10000 пассажиров пригородных поездов вычислена средняя дальность поездки – 32,4 км, среднеквадратическое отклонение – 10 км. Определить пределы средней дальности поездки m с вероятностью 0,954.
1) 32,2 ≤m≤ 32,6 2) 32,22 ≤m ≤32,62 3) 32,23≤ m ≤32,63
1.6. Для нормального распределения СВ всегда совпадают значения:
1) моды, медианы, математического ожидания;
2) моды и среднеквадратичного отклонения;
3) математического ожидания и среднеквадратичного отклонения.
1.7. Положительный знак парного коэффициента корреляции указывает на:
1) прямую зависимость между x и y;
2) обратную зависимость между x и y;
3) отсутствие зависимости между x и y.
1.8. Проверка гипотезы о значимости коэффициентов уравнения регрессии проводится по критерию:
1) Фишера; 2) 2 -Пирсона; 3) Стьюдента.
1.9. Для выделения тренда временного ряда можно использовать методы:
а) аналитический; б) геометрический; в) укрупнения интервалов.
1) а и в; 2) только а; 3) только б.
1.10. Для уравнения линейной регрессии, построенного по n=10 наблюдениям, значение коэффициента детерминации равно 0,8. Тогда значение статистики Фишера равно:
1) 4; 2) 32; 3) 2.
Вариант 2
2.1. Ряды распределения бывают:
1) интервальные; 2) вариационные; 3) номинальные.
2.2. Если все значения признака уменьшить на постоянную величину А, то дисперсия:
1) не изменится; 2) уменьшится на величину А; 3) увеличится на величину А.
2.3. Если все значения признака уменьшить в 10 раз, то дисперсия:
1) не изменится; 2) уменьшится в 10 раз; 3) уменьшится в 100 раз.
2.4. По данным значениям 
и числу наблюдений n=10 вычислить коэффициент вариации:
1) 2,5 2) 0,58 3) 3,71.
2.5. По данным выборочного обследования продолжительности телефонных разговоров по городской телефонной сети (100 наблюдений) установили, что средняя продолжительность телефонного разговора – 3 мин. при среднем квадратичном отклонении 2 мин. С вероятностью 0,954 определите продолжительности телефонного разговоров:
1) 2,6 ≤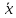 
≤ 3,4 2) 2,6 ≤ 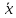≤ 3,0 3) 3,0 ≤ 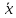≤ 3,4
2.6. При оценке плотности распределения используют:
1) гистограмму; 2) эмпирическую функцию распределения; 3) доверительный интервал.
2.7. Отрицательный знак парного линейного коэффициента корреляции указывает на:
1) отсутствие зависимость x и y; 2) обратную зависимость между x и y; 3) прямую зависимость между x и y.
2.8. Параметр b уравнения 
показывает:
1) на сколько в среднем изменится результат y, если фактор x изменится на натуральную единицу;
2) на сколько среднеквадратических отклонений изменится результат y, если фактор x изменится на 1 среднеквадратическое отклонение;
3) на сколько процентов изменится в среднем результат y, если фактор x изменится на 1
2.9. По критерию 
- Пирсона проверяется гипотеза:
1) о значимости коэффициентов уравнения регрессии; 2) о виде закона распределения случайной величины; 3) о значимости уравнения регрессии в целом.
2.10. Для уравнения эмпирической регрессии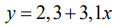 
значение статистики Стьюдента для коэффициента оказалось равным 4. Вычислить значение статистики Фишера F и сделать вывод о значимости уравнения в целом (на уровне значимости 0.05 ):
1) F=16, уравнение значимо; 2) F=2, уравнение значимо; 3) F=2, уравнение незначимо.
Вариант 3.
3.1. Что следует понимать под закономерностью распределения:
1) определенный порядок в изменении частот в соответствии с изменениями значений признака в вариационном ряду; 2) определенный порядок в значениях частот ряда распределения; 3) определенный порядок в значениях признака в вариационном ряду.
3.2. Дисперсия стажа нескольких рабочих равна 9 лет. Коэффициент вариации равен 0,3. Чему равняется средний стаж рабочих?
1) 30; 2) 10; 3) 2,7.
3.3. Если значение статистики критерия попало в критическую область, то гипотеза (на данном уровне значимости): 1) отвергается: 2) может быть принята; 3) вывод сделать нельзя.
3.4. По 10 выборочным наблюдениям вычислены значения 
. Значение выборочной оценки дисперсии равно:
1) 7,37 2) 7,3 3) 0,17.
3.5. Методом случайной повторной выборки было взято для проверки на вес 100 шт. деталей. В результате был установлен средний вес детали 30гр. при среднеквадратическом отклонении 4г. С вероятностью 0.954 требуется определить пределы, в которых находится средний вес деталей в m генеральной совокупности.
3.6. Для нормального закона распределения коэффициент асимметрии:
1) равен нулю; 2) меньше нуля; 3) больше нуля.
3.7. Коэффициент детерминации используются для выявления:
1) качества выбранной эконометрической модели; 2) незначимости коэффициентов регрессии; 3) отсутствия связи между зависимой и независимой переменными.
3.8. Отрицательный знак парного линейного коэффициента корреляции указывает на:
1) отсутствие зависимости x и y; 2) обратную зависимость между x и y; 3) прямую зависимость между x и y.
3.9. Гипотезу о среднем значении нормальной случайной величины проверяют по критерию:
1) Стьюдента; 2) 2 - Пирсона; 3) Фишера.
3.10. Для уравнения эмпирической регрессии y 1,7 + 2,3x значение статистики Стьюдента для коэффициента при x оказалось равным 3. Вычислить значение статистики Фишера F и сделать вывод о значимости уравнения в целом (на уровне значимости 0.05 ):
1) F=9, уравнение значимо; 2) F=4, уравнение значимо; 3) F=4, уравнение незначимо.
Вариант 4.
4.1. Полигоном распределения изображается:
1) интервальный ряд распределения; 2) эмпирическая функция распределения; 3) дискретный ряд распределения.
4.2. Средний стаж рабочих 5 лет. Коэффициент вариации 0,22. Чему равняется дисперсия стажа рабочих?
1) 1,1; 2) 1,21; 3) 0,05.
4.3. Коэффициент корреляции позволяет выявлять:
1) независимость случайных величин;
2) степень линейной зависимости между случайными величинами;
3) качество модели нелинейной регрессии.
4.4. По данным значениям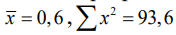 
и числу наблюдений n=10 вычислить коэффициент вариации:
1) 9 2) 5 3) 12
4.5. Станок-автомат штампует шайбы. При отборе 100 шайб вычислена средняя диаметров изготовленных образцов, равная 10,8 мм. С вероятностью 0,954 оценить средний размер диаметров m изготовленных шайб, если среднеквадратичное отклонение равно 2 мм.
4.6. Проверка гипотезы о виде закона распределения проводится по критерию: 1) 2 - Пирсона; 2) Фишера; 3) Стьюдента.
4.8. Коэффициент детерминации используется для:
1) оценки качества регрессионной модели; 2) оценки разброса случайной величины; 3) оценки тесноты связи между двумя случайными величинами.
4.9. Средний коэффициент эластичности показывает:
1) на сколько процентов изменится в среднем результат y, если фактор x изменится на 1 % от своего среднего;
2) на сколько в среднем изменится результат y, если фактор x изменится на натуральную единицу;
3) на сколько среднеквадратических отклонений изменится результат y, если фактор x изменится на одно среднеквадратическое отклонение.
4.10. Для уравнения линейной регрессии, построенного по n=12 наблюдениям, значение коэффициента детерминации равно 0,6. Тогда значение статистики Фишера равно:
1) 7,2; 2) 15; 3) 1,5.
Вариант 5
5.1. Вариационные ряды бывают:
1) интервальные и дискретные; 2) интервальные и моментные; 3) прерывные и непрерывные.
5.2. Эмпирическая средняя группы из 5 единиц составила 1.9, а группы численностью 10 единиц-1,75. Чему равняется эмпирическая средняя объединенной выборки?
1) 1,8 2) 1,825 3) 1,85
5.3. Оценкой разброса случайной величины являются: 1) эмпирическое среднее; 2) выборочное среднеквадратичное отклонение; 3) выборочная медиана.
5.4. По 50 выборочным наблюдениям вычислены значения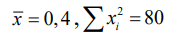 
. Значение выборочной дисперсии равно:
1) 2,1 2)1,2 3) 1,44
5.5. При проверке партии из 100 электроламп, вычислена средняя продолжительность горения лампы, которая оказалась равной 1000 часов. С вероятностью 0,954 найти пределы для средней продолжительности горения лампы, если среднеквадратическое отклонение горение лампы равно 40 часам?
5.6. Распределение времени обслуживания в системе массового обслуживания моделируется законом:
1) нормальным законом распределения; 2) показательным законом распределения; 3) равномерным законом распределения.
5.7. Если регрессионная модель содержит только одну объясняющую переменную, то она имеет название: 1) парной линейной регрессии; 2) парной регрессии; 3) множественной регрессии.
5.8. Коэффициент детерминации принимает значения: 1) от нуля до единицы; 2) неотрицательные; 3) от минус единицы до единицы.
5.9. Уравнение эмпирической регрессии имеет вид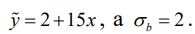 
Что можно сказать о значимости коэффициента b (на уровне значимости 0,05 ): 1) значим; 2) не значим; 3) неизвестно.
5.10. Для уравнения эмпирической регрессии 
значение статистики Стьюдента для коэффициента при x оказалось равным 2,5. Вычислить значение статистики Фишера F и сделать вывод о значимости уравнения в целом (на уровне значимости 0.05 ):
1) F=6,25, уравнение значимо; 2) F=2,5, уравнение не значимо; 3) F=6,25, уравнение незначимо.
Вариант 6.
6.1. Если каждое значение признака повторяется в ряду распределения один раз, то исчисляется:
1) средняя арифметическая простая;
2) средняя арифметическая взвешенная;
3) средняя гармоническая.
6.2. В бригаде шесть человек, имеющих стаж работы 2, 4, 5, 6, 7, 8, лет. Определите медиану:
1) 6;
2) 5;
3) 5,5.
6.3. Гипотеза о виде закона распределения является:
1) простой, непараметрической;
2) сложной, параметрической;
3) сложной, непараметрической.
6.4. По данным значениям x 0, 2 , 2 2 i x и числу наблюдений n=10 вычислить коэффициент вариации:
1) 0,8
2) 2
3) 0,5.
6.5. При проверке партии из 100 приборов, вычислена средняя продолжительность работы, которая оказалась равной 1000 часов. С вероятностью 0,954 найти пределы для средней продолжительности работы приборов, если среднеквадратичное отклонение работы 90 часам?
1) 982 m 1018
2) 981 m 1013
3) 986 m 1026 .
6.6. Число вызовов, поступающих в систему массового обслуживания в единицу времени, моделируется случайной величиной, имеющей:
1) распределение Пуассона;
2) нормальное распределение;
3) гипергеометрическое распределение.
6.7. Имеется следующая зависимость между расходами населения (у) и личным доходом (х): i x i y 250 0,1
. Укажите верную интерпретацию уравнения регрессии (показатели измерены в млн. руб.):
1) увеличение дохода на 1 млн. р. приведет к росту расходов на 100 т. руб.;
2) увеличение дохода на 1 м лн. р. не отразится на расходах населения;
3) увеличение дохода на 1 млн. р. увеличит расходы на 250 тыс. руб.
6.8. С помощью какого метода определяют коэффициенты уравнения регрессии:
1) метода наименьших квадратов;
2) метода Гаусса;
3) симплекс-метода.
6.9. Приведенная формула x k b y необходима для определения:
1) параметра уравнения регрессии;
2) коэффициента эластичности;
3) значимости коэффициента регрессии.
6.10. Для уравнения линейной регрессии, построенного по n=14 наблюдениям, значение коэффициента детерминации равно 0,9. Тогда значение статистики Фишера равно:
1) 0,75 ; 2) 108; 3) 12,6.
Вариант 7.
7.1. Эмпирическая функция распределения является:
1) непрерывной;
2) ступенчатой;
3) убывающей.
7.2. Модой в ряду распределения является:
1) значение признака, которое встречается чаще других;
2) значение признака, делящее ряд значений на две равные части;
3) наибольшее значение признака.
7.3. Среднее значение признака в двух совокупностях одинаково. Может ли быть различной вариация признака в этих совокупностях?
1) да;
2) нет.
7.4. По данным значениям 2 x , x 8 вычислить коэффициент вариации.
1) 4
2) 0,25
3) 0,75.
7.5. По данным выборочного обследования 10000 пассажиров пригородных автобусов, средняя дальность поездки – 32,4 км, среднеквадратическое отклонение – 10 км. Определить пределы средней дальности поездки с вероятностью 0,954.
1) 32, 2 m 32, 6
2) 32 m 32, 6
3) 31, 4 m 32,9
7.6. Для равномерного закона распределения коэффициент асимметрии:
1) больше нуля;
2) равен нулю;
3) меньше нуля.
7.7. Согласно методу наименьших квадратов, в качестве оценок коэффициентов регрессии следует использовать величины, которые минимизируют сумму квадратов отклонений:
1) фактических значений зависимой переменной от ее расчетных значений;
2) фактических значений зависимой переменной от ее среднего значения;
3) фактических значений объясняющей переменной от ее среднего значения.
7.8. Для оценки качества нелинейной регрессионной модели используют:
1) выборочную дисперсию;
2) индекс корреляции;
3) коэффициент асимметрии.
7.9. Коэффициент детерминации используется для:
1) оценки разброса случайной величины;
2) оценки качества регрессионной модели;
3) оценки тесноты связи между двумя случайными величинами.
7.10. Для уравнения эмпирической регрессии y x 7,8 3, 4 значение статистики Стьюдента для коэффициента оказалось равным 6. Вычислить значение статистики Фишера F и сделать при x вывод о значимости уравнения в целом (на уровне значимости 0.05 ):
1) F=36, уравнение значимо;
2) F=30, уравнение значимо;
3) F=36, уравнение незначимо.
Вариант 8.
8.1. Гистограмма применяется для графического изображения:
1) дискретных рядов распределения;
2) интервальных рядов распределения;
3) ряда накопленных частот.
8.2. Дисперсия признака - это:
1) отклонение отдельных значений признака от их среднего значения;
2) среднее значение суммы квадратов отклонений значений признака от среднего значения;
3) сумма квадратов отклонений значений признака от их среднего значения.
8.3. Гипотеза о величине математического ожидания является:
1) простой;
2) сложной, параметрической;
3) сложной, непараметрической.
8.4. По данным значениям x 1, 2 125 i x и числу наблюдений n=25 вычислить коэффициент вариации:
1) 2
2) 4
3) 0,5.
8.5. Станок-автомат штампует валики. При отборе 100 валиков вычислена средняя диаметров изготовленных образцов равная 16,8 мм. С вероятностью 0,954 оценить средний размер диаметров изготовленных валиков, если среднеквадратичное отклонение равно 5мм.
1) 15,8 m 17,8
2) 15, 6 m 17, 0
3) 16, 4 m 17, 4.
8.6. Для оценки плотности распределения используют:
1) гистограмму;
2) эмпирическую функцию распределения;
3) доверительный интервал.
8.7. Регрессия называется парной линейной регрессией, если ее уравнение содержит:
1) две зависимых переменных;
2) одну независимую переменную, связанную линейной зависимостью с зависимой переменной;
3) две зависимых и одну независимую переменную.
8.8. Коэффициент детерминации принимает значения:
1) любые неотрицательные значения;
2) от минус единицы до единицы;
3) от нуля до единицы.
8.9. По критерию 2 -квадрат Пирсона проверяется гипотеза:
1) о значимости коэффициентов уравнения регрессии;
2) о виде закона распределения случайной величины;
3) о значимости уравнения регрессии в целом.
8.10. Для уравнения линейной регрессии, построенного по n=20 наблюдениям, значение коэффициента детерминации равно 0,85. Тогда значение статистики Фишера равно:
1) 5,67;
2) 102;
3) 0,314.
Вариант 9.
9.1. Полигоном распределения изображается:
1) интервальный ряд;
2) ряд накопленных частот;
3) дискретный ряд.
9.2. Модой в ряду распределения является:
1) значение признака, делящее ряд ранжированных значений на две равные части;
2) наибольшее значение признака;
3) значение признака, которое встречается чаще других.
9.3. Оценка параметра случайной величины является состоятельной, если:
1) предел оценки по вероятности равен истинному значению параметра генеральной совокупности;
2) ее среднее значение равно оцениваемому параметру;
3) оценка имеет наименьшую дисперсию при данном объеме выборки.
9.4. По 20 выборочным наблюдениям вычислены значения x 0,3, 2 80 i x . Значение выборочной дисперсии равно:
1) 3,7
2) 3,91
3) 0,11.
9.5. По данным выборочного обследования продолжительности телефонных разговоров по городской телефонной сети (100 наблюдений) установили, что средняя продолжительность телефонного разговора – 4 мин. при среднем квадратичном отклонении 2 мин. С вероятностью 0,954 оцените среднюю продолжительности телефонного разговоров.
1) 3, 6 m 4, 4;
2) 3, 6 m ;4, 2
в) 3, 4 m 4, 4.
9.6. Для показательного закона распределения коэффициент асимметрии:
1) равен нулю;
2) больше нуля;
3) меньше нуля.
9.7. Выберите уравнение регрессии, в котором связь между y и x обратная:
1) y = -6 + 9*x1
2) y = 6 – 9*x1
3) y = -6 +8*x1
9.8. Значения какого из показателей заключены в интервале от минус единицы до единицы:
1) ковариация;
2) парный коэффициент корреляции;
3) коэффициент детерминации.
9.9.По критерию Фишера проверяется гипотеза:
1) о значимости уравнения регрессии в целом;
2) о значимости коэффициентов уравнения регрессии;
3) о виде закона распределения.
9.10. Для уравнения эмпирической регрессии y x 0,1 0,81 значение статистики Стьюдента для коэффициента оказалось равным 5. Вычислить значение статистики Фишера F и сделать при x вывод о значимости уравнения в целом (на уровне значимости 0.05 ):
1) F=25, уравнение значимо;
2) F=20, уравнение значимо;
3) F=25, уравнение незначимо.
Вариант 10.
10.1. Значения эмпирической функции распределения изменяются в пределах:
1) [-1;1] 2) [0;1] 3) [0;∞].
10.2.Характеристиками положения случайных величин являются:
1) математическое ожидание и медиана;
2) математическое ожидание и дисперсия;
3) мода и среднеквадратичное отклонение.
10.3. Несмещенной оценкой дисперсии случайной величины является:
1) выборочная дисперсия;
2) статистика s 2 ;
3) выборочное среднеквадратичное отклонение.
10.4. По данным значениям x 0,31, 2 6 i x и числу наблюдений n=32 вычислить коэффициент вариации (округлив до сотых):
1) 1,33 2)5,33 3) 0,75.
10.5. По данным 100 измерениям вычислены: среднее значение длин деталей, равное 42,2мм, и исправленное среднеквадратичное отклонение, равное 8мм. С вероятность 0,954 оцените среднюю длину деталей.
1) 40, 6 m 43,8 2) 40,4 m 43, 6 3) 41, 2 m 43, 2 .
10.6. Сезонные индексы измеряются:
1) в долях; 2) в процентах; 3) в натуральных единицах.
10.7. Уравнение регрессии имеет вид: 5,1 1, 7 i i y x . На сколько единиц своего измерения в среднем изменится Y при увеличении X на 1 единицу своего измерения:
1) увеличится на 1,7 2) не изменится; 3) уменьшится на 1,7.
10.8. Средняя урожайность кукурузы по области – 28 ц/га, дисперсия –49. Средняя урожайность ржи – 20 ц/га, дисперсия –25. Сравните между собой вариация урожайности пшеницы и ржи:
1) вариация урожайности кукурузы выше;
2) вариация урожайности ржи выше;
3) вариация урожайности одинаковая;
10.9. Какой критерий используют для оценки значимости уравнения регрессии:
1) критерий Фишера;
2) критерий Стьюдента;
3) критерий 2 - Пирсона.
10.10. Для уравнения линейной регрессии, построенного по n=8 наблюдениям, значение коэффициента детерминации равно 0,99. Тогда значение статистики Фишера равно:
1) 99; 2) 594; 3) 16,5.