ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.03.2024
Просмотров: 30
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ЗАКЛЮЧЕНИЕ
Актуальностью темы является то, что социальная статистика играет очень важную роль в жизни каждого человека, потому что являются непосредственным источником удовлетворения его неограниченных потребностей.
Важной задачей статистики является изучение изменений анализируемых показателей во времени. Эти изменения можно изучить, если иметь данные по определенному кругу показателей на ряд моментов времени или за ряд промежутков времени, следующих друг за другом. Ряд расположенных в хронологической последовательности значений статистических показателей представляет собой временной (динамический) ряд. Каждый временной ряд состоит из 2-х элементов:
- указываются моменты или периоды времени, к которым относятся приводимые статистические данные;
- приводятся статистические показатели, которые характеризуют изучаемый объект на определенный момент или за указанный период.
ЗАДАЧИ
Задача 1. Денежные доходы населения России в январе-июне 1994 г. составили (млрд. руб.)
| январь | февраль | март | апрель | май | июнь |
| 14128 | 18155 | 21612 | 23909 | 23517 | 27670 |
а) Определить:
- цепные абсолютные приросты, темпы роста и прироста;
- среднемесячный доход населения в первом полугодии 1994 г.;
- среднемесячные темпы роста и прироста денежных доходов населения в первом полугодии.
б) Указать вид ряда динамики;
в) Представить исходные и расчетные данные в виде таблицы.
Решение: Данный ряд является интервальным рядом абсолютных величин.
1. Определим цепные показатели динамики
- абсолютный прирост Δ уi = yi – yi-1, (млрд. руб.)
где уi – i-ый уровень ряда динамики;
Уi-1 – уровень ряда, предшествующий i-му.
Δy1 = 18155 – 14128 = 4027
Δy2 = 21612 – 18155 = 3457
Δy3 = 23909 – 21612 = 2297
Δy4 = 23517 – 23909 = -392
Δy5 = 27670 – 23517 = 4153
-
темпы роста Тi (%) Ti = yi/ yi-1 * 100%
Т1 = 18155: 14128* 100 = 128,5
Т2 = 21612: 18155* 100 = 119,0
Т3 = 23909: 21612* 100 = 110,6
Т4 = 23517: 23909* 100 = 98,4
Т5 = 27670: 23517* 100 = 117,7
- темпы прироста ΔТi = Тi – 100% (%)
ΔT1 = 128,5 – 100 = 28,5
ΔT2 = 119,0 – 100 = 19,0
ΔT3 = 110,6 – 100 = 10,6
ΔT4 = 98,4 – 100 = -1,6
ΔT5 = 117,7 – 100 = 17,7
2. Вычислим среднемесячный доход населения в первом полугодии 1994 года по формуле средней арифметической простой
Уср = (у1+ у2+…+уn): n
Уср = ( 14128+18155+21612+23909+23517+27670): 6 = 21498,5 млрд. руб.
3. Вычислим среднемесячные темпы роста и прироста
Тср = n√yn: y0 * 100% ΔTcp = Tcp – 100%
Tcp = 5√27670: 14128* 100% = 114,1%
ΔTcp = 114,1 – 100 = 14,1%
Таким образом, наибольший месячный прирост доходов населения произошло в июне месяце по сравнению с маем месяцем (прирост месячных доходов населения составил 4153 млрд. руб. или 17,7%), в мае месяце по сравнению с апрелем произошло сокращение доходов населения на 392 млрд. руб. или на 1,6%. Среднемесячный доход населения РФ в 1-м полугодии 1994 года составил 21498,5 млрд. руб. В среднем за месяц доходы населения увеличивались на 14,1%.
Представим исходные и расчетные показатели в таблице.
| Месяц | Денежные доходы, млрд. руб. | Цепные показатели | ||
| Абсолютный прирост, млрд. руб. | Темп роста, % | Темп прироста, % | ||
| Январь | 14128 | - | - | - |
| Февраль | 18155 | 4027 | 128,5 | 28,5 |
| Март | 21612 | 3457 | 119,0 | 19,0 |
| Апрель | 23909 | 2297 | 110,6 | 10,6 |
| Май | 23517 | -392 | 98,4 | -1,6 |
| Июнь | 27670 | 4153 | 117,7 | 17,7 |
| Среднемесячный доход населения уср = 21498,5 млрд.руб. | ||||
| Среднемесячный темп роста Тср = 114,1% | ||||
| Среднемесячный темп прироста ΔТср = 14,1% | ||||
Задача 2. Имеются данные по 10 семьям об уровне доходов на 1 человека в год (Х) и покупательском спросе-расходах на одежду на 1 чел. в год (У), в млн. руб. Методом корреляционного анализа исследовать зависимость между этими признаками. Написать уравнении регрессии, построить эмпирические точки и линию регрессии. Найти коэффициенты корреляции и детерминации. Сформулировать выводы по результатам анализа.
| 3,9 | 2,2 | 3,9 | 4,2 | 4,1 | 1,8 | 4,9 | 2,3 | 5,0 | 3,2 |
| 0,23 | 0,15 | 0,20 | 0,28 | 0,25 | 0,13 | 0,28 | 0,15 | 0,29 | 0,20 |
Решение: Составим рабочую таблицу
| № п/п | Х | У | Х*Х | У*У | Х*У |
| 1 | 3,9 | 0,23 | 15,21 | 0,0529 | 0,897 |
| 2 | 2,2 | 0,15 | 4,84 | 0,0225 | 0,33 |
| 3 | 3,9 | 0,2 | 15,21 | 0,04 | 0,78 |
| 4 | 4,2 | 0,28 | 17,64 | 0,0784 | 1,176 |
| 5 | 4,1 | 0,25 | 16,81 | 0,0625 | 1,025 |
| 6 | 1,8 | 0,13 | 3,24 | 0,0169 | 0,234 |
| 7 | 4,9 | 0,28 | 24,01 | 0,0784 | 1,372 |
| 8 | 2,3 | 0,15 | 5,29 | 0,0225 | 0,345 |
| 9 | 5 | 0,29 | 25 | 0,0841 | 1,45 |
| 10 | 3,2 | 0,2 | 10,24 | 0,04 | 0,64 |
| Сумма | 35,5 | 2,16 | 137,49 | 0,4982 | 8,249 |
Уравнение регрессии будем искать в виде линейной связи у = а*х + в Параметры уравнения регрессии вычислим методом наименьших квадратов из системы линейных уравнений:
n*b + a* ∑x = ∑ y
b*∑x + a* ∑x2 = ∑x*y
Тогда 10b + 35,5 a = 2,16
35,5b + 137,49a = 8,249
Решаем данную систему
b = 0,216 – 3,55a
7,768 – 126,025a + 137,49a = 8,249
b = 0,035
a = 0,035
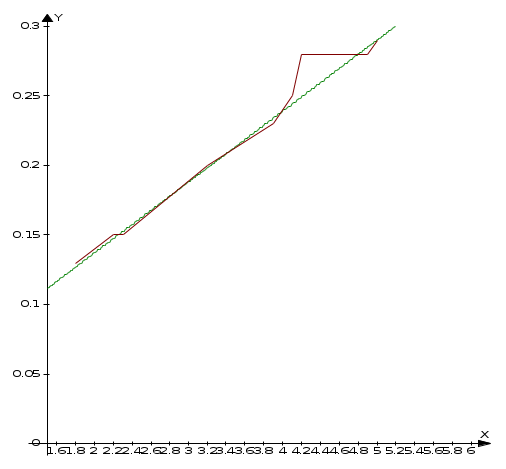
Уравнение регрессии имеет вид у = 0,035 + 0,051*х
Таким образом, с увеличением доходов на 1 млн. руб. спрос- расходы на одежду на 1 человека увеличиваются на 51 тыс. руб.
Построим графики эмпирических точек и линии регрессии.
2. Вычислим коэффициенты корреляции и детерминации.
r = [ хуср – хср * уср.]: x : y
хуср = 8,249:10 = 0,8249
хср = 35,5: 10 = 3,55
уср = 2,16: 10 = 0,216
х = 137,49: 10 – 3,552 = 1,071
у = 0,4982:10 – 0,2162 = 0,056
Коэффициент корреляции равен
r = ( 0,8249 – 3,16*0,216): 1,071: 0,056 = 0,969
Коэффициент детерминации равен
D = r2 * 100% = 0,9692 * 100% = 93,8%
Таким образом, связь между уровнем доходов на 1 человека в го и покупательском спросе-расходах на одежду на 1 человека в год тесная, прямая (коэффициент корреляции близок к 1 и больше нуля). 93,8% изменений покупательского спроса-расходов вызвано изменением уровня доходов на 1 человека в год.
Задача 3. По данным 10%-го выборочного обследования распределение семей в районе по численности детей характеризуется следующими данными:
| Число детей | 0 | 1 | 2 | 3 | 4 | 5 | 6 | Всего |
| Число семей | 5 | 28 | 22 | 19 | 15 | 5 | 6 | 100 |
С вероятностью 0,954 определить ошибку выборки для среднего числа детей в семье. Какая должна быть численность выборки, чтобы ошибка выборки уменьшилась в 1,5 раза?
Решение:
1. Вычислим среднее число детей в выборке, используя формулу средней арифметической взвешенной:
Хср = ∑хi fi :∑fi,
где xi – число детей;
fi – число семей
Хср = (0*5+1*28+2*22+3*19+4*15+5*5+6*6): 100 = 2,78 детей
Дисперсию вычисли по формуле: σ2 = ∑(х-хср)2 fi :∑fi
σ2 = [(0-2,78)2
*5+(1-2,78)2*28+(2-2,78)2*22+(3-2,78)2*19+(4-2,78)2*15+(5-2,78)2*5+(6-2,78)2*:6]: 100 = 250,84: 100 = 2,508
Предельную ошибку для бесповторного отбора вычислим по формуле:
Δ = t* √σ 2/.n * (1 – n/ N)
t = 2,0 – нашли по таблице Лапласа
n/ N = 0,1 – 10% -ая выборка
Δ = 2* √2,508: 100 * (1 – 0,1) = 0,3
Предельная ошибка выборки составила 0,3 детей.
2. Определим численность выборки, если предельная ошибка сократилась в 1,5 раза .Δ = 0,3: 1,5 = 0,2 N = 1000 cемей (100: 0,1)
N = [t2*σ2 * N]/ [Δ2*N + t2*σ2]
N = [22 * 2,508*1000]: [0,22* 1000 + 22 *2,508] = 200,51= 201 семья
Чтобы предельная ошибка уменьшилась в 1,5 раза необходимо отобрать в выборку 201 семью.
Задача 6. Имеются следующие данные о продаже товаров за два периода:
| Вид товара | Сумма товарооборота за отчетный период, млн. руб., p1q1 | Изменение цен в отчетном периоде по сравнению с базисным, % |
| А | 820 | +8,2 |
| Б | 560 | +6,1 |
| В | 120 | +1,4 |
Определить :
-
Изменение цен по трем видам продукции в среднем. -
Сумму потерь населения в связи с ростом цен.
Решение: 1. Воспользуемся формулой общего индекса цен
Ip = ∑p1*q1: ∑p0*q1 = Ip = ∑p1*q1: ∑p1*q1/ip
Ip = (820+560+120): (820: 1,082+560:1,061+120:1,014) = 1500: 1404 = 1,068 (106,8%)
Таким образом, в среднем цены по трем видам продукции в отчетном периоде по сравнению с базисным периодом увеличились на 6,8%.
2. Определим сумму потерь населения: Δ = ∑p1*q1: ∑p0*q1
Δ = 1500 – 1404 = 96 млн. руб.
Сумма потерь населения в связи с ростом цен составила 96 млн. руб.
Заключение
В ходе проделанной работы собран и структурирован материал о статистическом изучении расходов населения.
Актуальностью темы является то, что потребительские расходы играют очень важную роль в жизни каждого человека, потому что являются непосредственным источником удовлетворения его неограниченных потребностей.
Важной задачей статистики является изучение изменений анализируемых показателей во времени. Эти изменения можно изучить, если иметь данные по определенному кругу показателей на ряд моментов времени или за ряд промежутков времени, следующих друг за другом. Ряд расположенных в хронологической последовательности значений статистических показателей представляет собой временной (динамический) ряд. Каждый временной ряд состоит из 2-х элементов:
